문제
규칙을 찾는 문제
저는 스택을 사용했습니다.
-
드래곤 커브는 세가지 속성을 가집니다.
1) 시작 점
2) 시작 방향
3) 세대즉, K(K > 1)세대 드래곤 커브는
K-1세대 드래곤 커브를끝 점을 기준으로 90도 시계 방향 회전시킨 다음, 그것을끝 점에 붙인 것입니다. -
n 드래곤 커브의 개수 N(1 ≤ N ≤ 20)
-
x, y 드래곤 커브의 시작점 (0 ≤ x, y ≤ 100)
(좌표 평면의x축은 → 방향,y축은 ↓ 방향입니다) -
d 시작 방향 (0 ≤ d ≤ 3)
0) x좌표가 증가하는 방향 (→)
1) y좌표가 감소하는 방향 (↑)
2) x좌표가 감소하는 방향 (←)
3) y좌표가 증가하는 방향 (↓) -
g 세대 (0 ≤ g ≤ 10)
-
드래곤 커브는 격자 밖으로 벗어나지 않습니다. 드래곤 커브는 서로 겹칠 수 있습니다.
-
크기가 100×100인 격자 위에 드래곤 커브가 N개 있습니다.
-
크기가 1×1인 정사각형의 네 꼭짓점이모두 드래곤 커브의 일부인정사각형의 개수를 구하시오.
1. 첫인상
아 뭐야, 왜이렇게 복잡해, 할 수 있을까...
우리 모두 할 수 있어요!
이럴수록 침착하게. 손으로 그려봅시다.
2. 드래곤 커브 생성 규칙
1) 0 세대
(0, 0)시작 → (1, 0) 끝
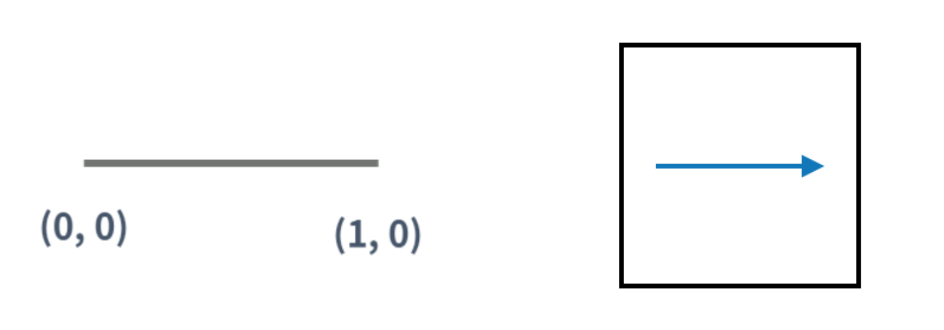
2) 1 세대
(0,0) 시작 → ↑ (1, -1) 끝
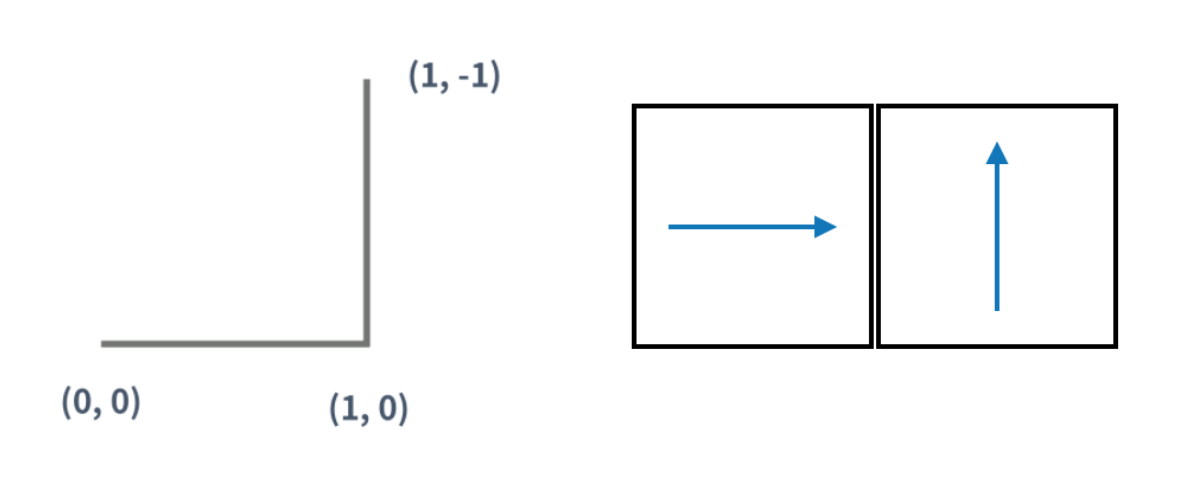
2) 2 세대
(1, -1) 시작→ ↑ ← ↑ (0, 2) 끝
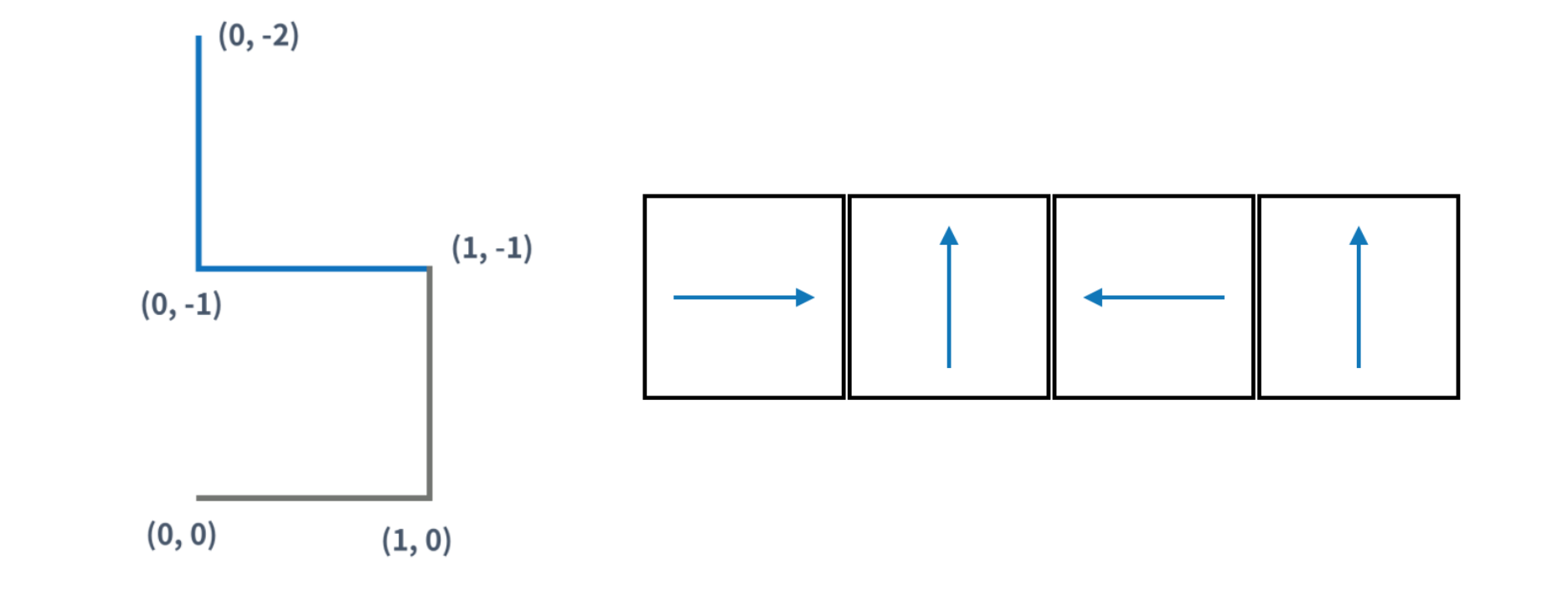
3) 3 세대
(0, -2) 시작 ← ↓ ← ↑ (-2, 2) 끝
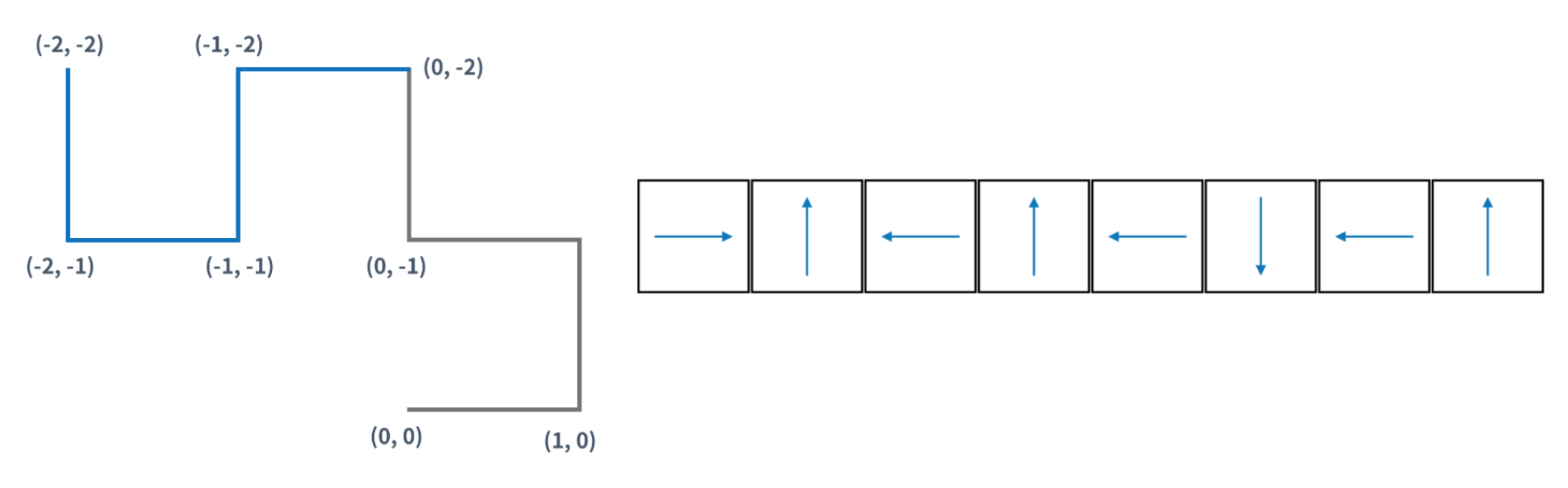
4) 생각 해보기
근데 여기서 2세대와 비교하면서 다음과 같이 나눌 수 있습니다.
1) 3세대는 2세대의 뒤에서 부터 꺼내면서 만든다.
2) 그리고 그 규칙이 있는데
↑ 는 ← 이 되고
← 는 ↓ 이 되고
↓ 는 → 이 되고
→ 는 ↑ 이 됩니다.
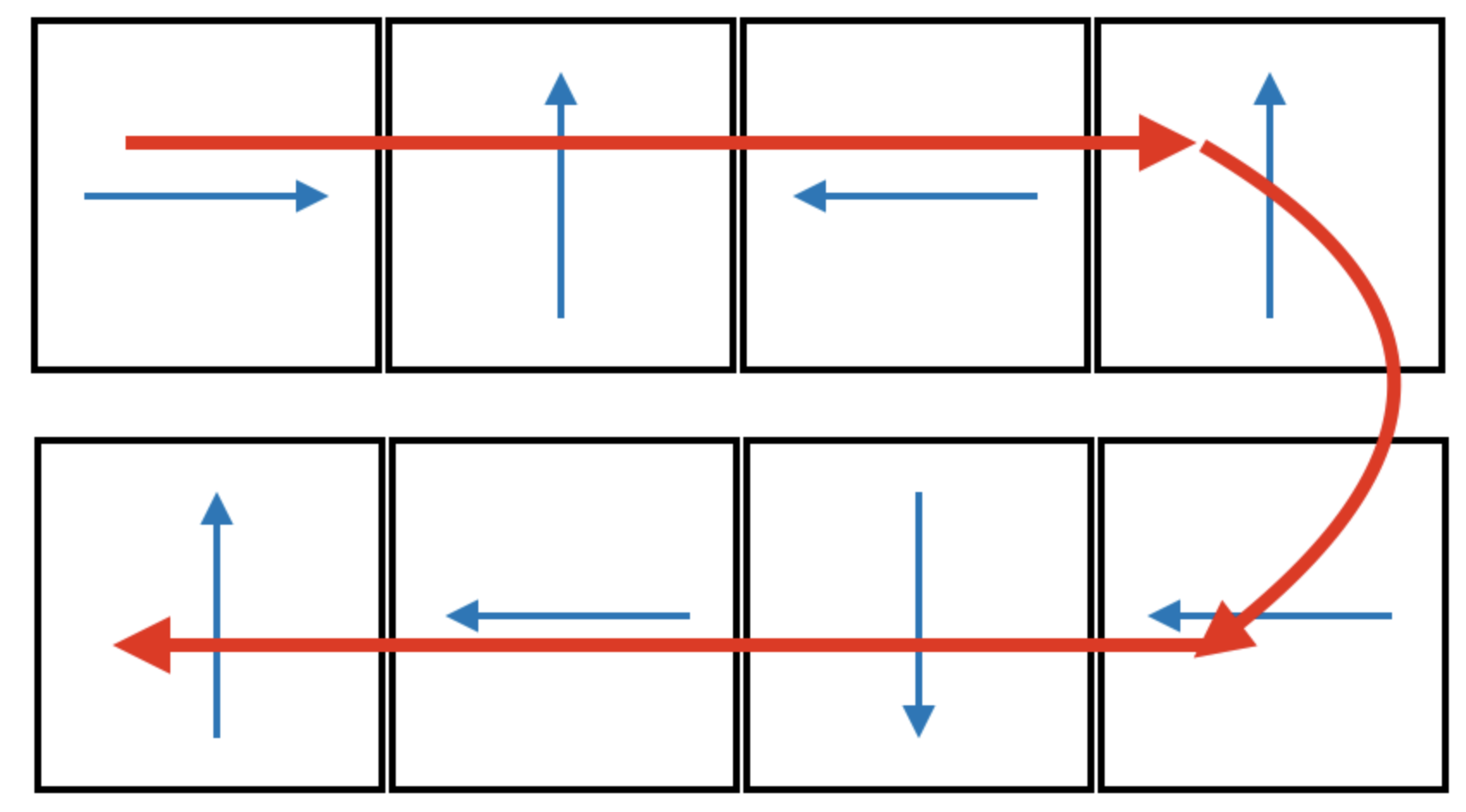
5) 방향
방향은 0~3 이고
1 은 2가 되고
2 는 3이 되고
3 은 0이 되고
0 은 1이 됩니다.
이것을 일반화 하면 다음과 같습니다.
dir = (dir + 1) % 4;
3. 규칙 정리
1) 현제 세대를 만드는 방법
1) 이전 세대의 끝점에서 시작
2) 이전 세대의 뒤에서 부터 꺼내면서 dir = (dir + 1) % 4; 규칙에 따라 방향을 변환합니다.
3) 그리고, 변환하면서 만든 방향 정보를 넣어서 다음 세대를 만들 수 있도록 합니다.
2) 필요한것 2개
1) 이전 세대의 끝점의 정보
2) 이전 세대의 방향정보를 넣을 자료구조 (스택)
(무엇인가를 뒤에서 꺼낼때, 가장 아름답게 꺼내는 자료구조는 스택입니다. )
4. 사각형의 개수
어떻게 사각형의 개수를 셀 것인가?
2차원 배열에서 왼쪽 상단을 기준으로 인접한 4칸을 모두 조사합니다.
모두 표시가 되어있으면, 개수를 1증가시킵니다.
//100*100 2차원 행렬을 2중 for문 사용한 단순한 탐색
//인접한 4칸이 모두 true이면, 4칸이 모두 드래곤 커브의 일부인것
//갯수를 1증가시킨다.
int result = 0;
for(int i=0; i<99; i++){
for(int j=0; j<99; j++){
//인접한 4칸의 정사각형이 모두 드래곤의 일부이면
if(map[i][j] == true && map[i][j+1] == true && map[i+1][j] == true && map[i+1][j+1] == true){
//갯수를 1 증가시킨다.
result++;
}
}
}5. 주의할 점
보통 알고리즘 문제에서 좌표를 제공할때 (세로, 가로) 순서로 제공합니다.
단, 이 문제의 x,y는 순서가 (가로, 세로)입니다. 따라서, 순서를 바꿔서 입력받겠습니다.
6. 시간 복잡도 계산
최대 n(20)개의 드래곤 커브를 만들어야 하고
각각의 드래곤 커브는 g(10)세대 까지 있습니다.
=> n*2^g
이후 xy (100 100) 크기의 2차원 배열을 2중 for문으로 탐색합니다.
따라서 시간복잡도는 n2^g + 100100
(엄밀하게 말하면 0세대 부터 10세대를 모두 만들기 때문에 2^0 + 2^1 ... 2^10 = 2047인데 1024랑 별로 차이 안나서 그냥 n*2^g 이라고 했습니다.)
하여튼, 2047 + 10000 => 12047 시간안에 충분히 풀 수 있습니다.
7. 코드
1) c++
#include <iostream>
#include <vector>
#define max_int 101
using namespace std;
//시간 복잡도: O(n*2^g + xy)
//공간 복잡도: O(xy + n)
//사용한 알고리즘: 반복문
//사용한 자료구조: 스택(벡터), 2차원 배열
int n, x, y, d, g, result;
//끝점의 정보
int end_x, end_y;
bool map[max_int][max_int];
//왼쪽, 위쪽, 오른쪽, 아래쪽
int dx[] = {0, -1, 0, 1}, dy[] = {1, 0, -1, 0};
//이전 세대의 방향정보를 저장하는 스택
//stl 스택쓰면 귀찮으니까 인덱스로 접근 할 수 있는 벡터를 사용한다.
vector<int> dragon;
//스택을 조사하면서 드래곤 커브를 만드는 함수
void make_generation(vector<int> &dragon){
//현재 스택의 크기를 먼저 계산해 놓는다.
int size = (int)dragon.size();
//스택의 뒤에서 부터 꺼내면서
//다음세대의 방향정보를 dir = (dragon[i] + 1)%4; 규칙에 따라 생성한다.
for(int i=size-1; i>=0; i--){
int dir = (dragon[i] + 1)%4;
//다음 세대의 방향정보를 바탕으로 다음 x,y를 찾고 이를 갱신한다.
end_x = end_x + dx[dir];
end_y = end_y + dy[dir];
//만들어진 드래곤 커브를 지도에 놓아준다.
map[end_x][end_y] = true;
//다음세대를 위하 스택에 방향정보를 넣어준다.
dragon.push_back(dir);
}
}
int main(){
scanf("%d", &n);
for(int i=0; i<n; i++){
//x, y의 순서를 바꿔서 입력받는다.
int y, x, d, g;
scanf("%d %d %d %d", &y, &x, &d, &g);
//기존 드래곤 커브의 스택을 비워준다.
dragon.clear();
//시작점에에 드래곤 커브가 놓여있으므로 지도에 표시해준다.
map[x][y] = true;
//0세대는 미리 만들어 놓는다.
end_x = x + dx[d];
end_y = y + dy[d];
//0세대를 만든 이후에도 지도에 표시해준다.
map[end_x][end_y] = true;
//0세대의 방향정보를 스택에 넣어준다.
dragon.push_back(d);
//반복문을 통해 0부터 차례차례 드래곤 커브를 만들면서 g세대까지 만든다.
for(int i=0; i<g; i++){
//드래곤 커브를 만들자
make_generation(dragon);
}
}
//100*100 2차원 행렬을 2중 for문 사용한 단순한 탐색
//인접한 4칸이 모두 true이면, 4칸이 모두 드래곤 커브의 일부인것
//갯수를 1증가시킨다.
for(int i=0; i<=max_int-2; i++){
for(int j=0; j<=max_int-2; j++){
//인접한 4칸의 정사각형이 모두 드래곤의 일부이면
if(map[i][j] == true && map[i][j+1] == true && map[i+1][j] == true && map[i+1][j+1] == true){
//갯수를 1 증가시킨다.
result++;
}
}
}
//갯수 출력
printf("%d\n", result);
}
2) python3
max_int = 101
end_x = 0
end_y = 0
dx = [0, -1, 0, 1]
dy = [1, 0, -1, 0]
dragon = []
result = 0
a = [[False for col in range(max_int)] for row in range(max_int)]
n = int(input())
def make_genration():
size = len(dragon)
for i in range(size-1, -1, -1):
dir = (dragon[i] + 1) % 4
global end_x, end_y
end_x = end_x + dx[dir]
end_y = end_y + dy[dir]
a[end_x][end_y] = True
dragon.append(dir)
for i in range(n):
y, x, d, g = map(int, input().split())
dragon.clear()
end_x = x
end_y = y
a[end_x][end_y] = True
end_x = x + dx[d]
end_y = y + dy[d]
a[end_x][end_y] = True
dragon.append(d)
for i in range(g):
make_genration()
for i in range(max_int - 1):
for j in range(max_int - 1):
if a[i][j] and a[i+1][j] and a[i][j+1] and a[i+1][j+1]:
result += 1
print(result) 
