빨간색, 파란색 고르는것은 항상 매트릭스가 생각나

두개의 버튼

n에서 m을 만들기 위한 최소 버튼 클릭수를 계산하는 문제

내 마음대로 번역

바시야(Vasya)는 신기한 장치를 찾았습니다.

패널의 앞부분은 빨간 버튼, 파란 버튼, 양의 정수를 보여주는 디스플레이가 있습니다.

1) 빨간 버튼을 누르면, 장치는 디스플레이의 숫자에 2를 곱합니다.
2) 파란 버튼을 누르면, 장치는 디스플레이의 숫자에서 1을 뺍니다.

숫자가 양의 정수가 아니면 장치가 고장납니다.

디스플레이는 충분히 큰 숫자를 보여줄 수 있습니다.
처음 디스플레이는 n을 보여주었습니다.

밥(Bob)은 숫자 m을 디스플레이에 보여주고 싶습니다. 목적을 달성하기 위한 최소 버튼 클릭수는 몇번입니까?

n, m (1 ≤ n, m ≤ 10000) (n은 처음 보여주는 숫자, m은 만들고 싶은숫자)

• 시간 제한 2초
• 문제 링크

---

풀이 과정

1. 접근 과정

그래프

생각을 넓혀보자요.

시작점을 n, 도착점을 m으로 생각하면

이 문제는 최단 경로를 찾는 문제로 바꿀 수 있습니다.

따라서, 버튼 클릭수는 시작점에서 도착점까지의 거리입니다.

그래, 이 문제는 그래프 같지 않는 그래프문제

2. 그래프 설계

그래프는 정점과 간선으로 이루어진 자료구조입니다.
정점 x를 1이상 n이하의 양의 정수라면, 간선은 1) 빨간 버튼, 2) 파란 버튼이 됩니다.

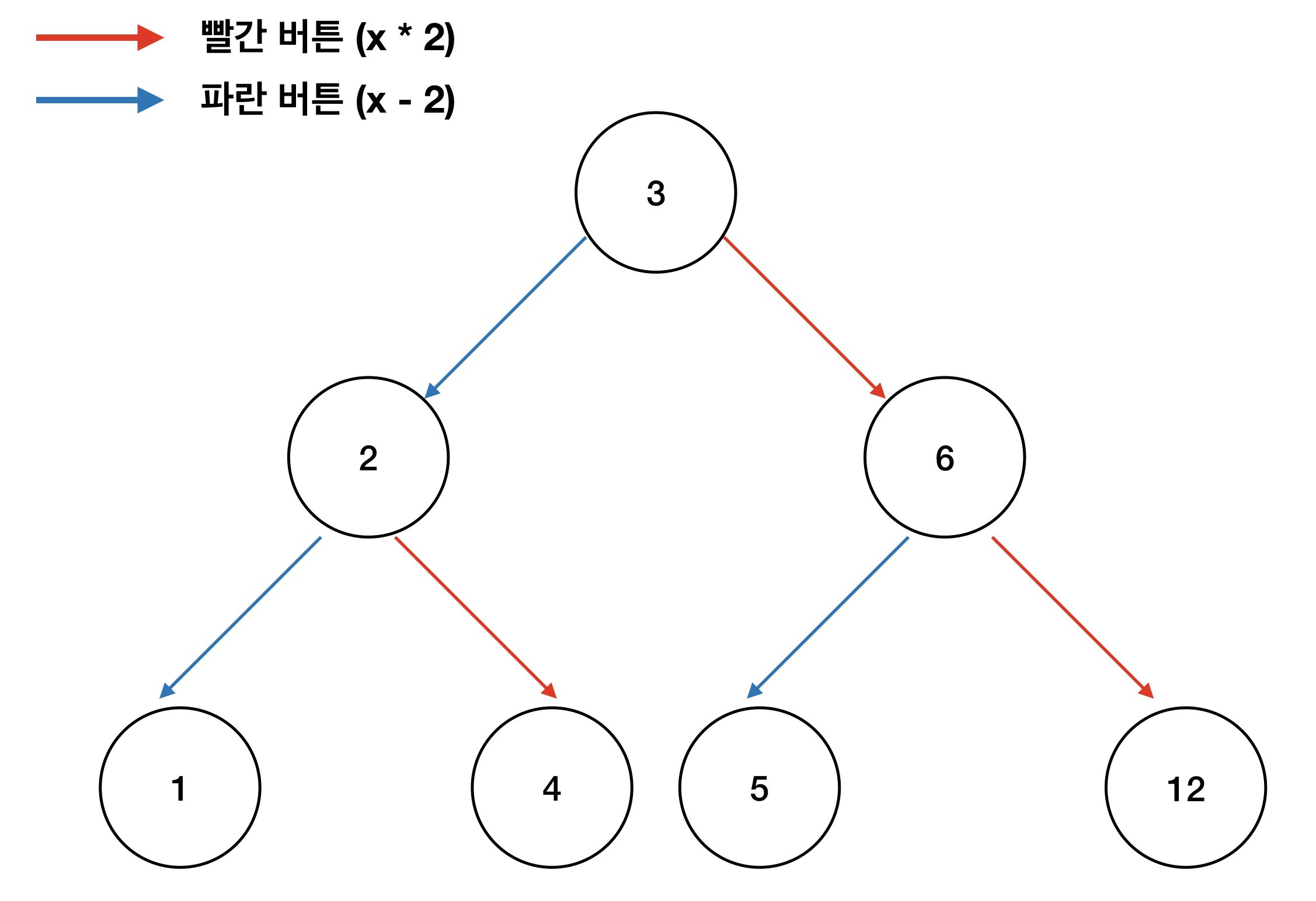
3. BFS

근데 왜 BFS로 푸냐면,
BFS는 모든 간선의 가중치가 1로 같을때 최단경로를 찾아줍니다.
먼저 도착한 경로가 제일 빠른 경로

이 문제에서 가중치는 클릭 1번, 빨간 버튼을 누르든, 파란 버튼을 누르든 딱 한번만 눌러서 다른 수로 이동할 수 있습니다.

4. 주의 사항

n(시작점) 3, m(도착점) 5라고 할때
빨간버튼 한번, 파란버튼 한번 눌러서 최소 2번 클릭만에 갈 수 있습니다.
3 * 2 - 1 = 5

3 * 2 하는 순간 숫자가 5를 넘어갑니다.

이것을 고려하고
배열을 사용하는 경우 범위를 잘못 지정하면 segmentation fault 에러가 발생할 수 있기 때문에

저는 20001 크기의 배열을 사용했습니다. 원래 n제한은 10000

5. 시간 복잡도 계산

0) n 제한은 10000

1) BFS의 시간 복잡도는 O(V+E) (V: 정점의 수, E: 간선의 수)

2) 여기서 V는 n, E는 2n

3) 총 걸리는 시간은 O(n), 시간안에 풀 수 있습니다.

코드

1. C++

#include <iostream>
#include <queue>
#define max_int 20001

using namespace std;

/*
 시간 복잡도: O(n)
 공간 복잡도: O(n)
 사용한 알고리즘: BFS
 사용한 자료구조: 큐
 */

int start_node, end_node, check[max_int];

void bfs() {
    // 큐를 만들어 줍니다.
    queue<int> q;
    // 시작점을 0으로 만들어서, 거리는 0이고, 방문했음을 표시합니다.
    check[start_node] = 0;
    q.push(start_node);
    
    while (!q.empty()) {
        int node = q.front();
        q.pop();
        
        int next;
        // 1) 빨간 버튼 (양의 정수 * 2 를 수행합니다.)
        next = node * 2;
        // 여기 주의!!!
        // 값에 대한 범위검사가 앞으로 &&연산의 첫번째로 와야합니다.
        // 첫번째를 통과하지 않은 값이을 check배열에 넣으면 segmentation fault에러가 발생합니다.
        // (범위에 없는 인덱스를 통해 배열 참조)
        // && 연산은 첫번째가 false이면 두번째는 검사하지 않습니다.
        if (next <= end_node * 2 && check[next] == -1) {
            check[next] = check[node] + 1;
            q.push(next);
        }
        
        // 2) 파란버튼 (양의 정수 - 1 를 수행합니다.)
        next = node - 1;
        // 여기 주의!!!
        // 값에 대한 범위검사가 앞으로 &&연산의 첫번째로 와야합니다.
        // 첫번째를 통과하지 않은 값이을 check배열에 넣으면 segmentation fault에러가 발생합니다.
        // (범위에 없는 인덱스를 통해 배열 참조)
        // && 연산은 첫번째가 false이면 두번째는 검사하지 않습니다.
        // 문제에서 양의 정수가 아니면, 장치가 고장난다고 했습니다.
        if (next > 0 && next < max_int && check[next] == -1) {
            check[next] = check[node] + 1;
            q.push(next);
        }
    }
}


int main() {
    // 1. 입력
    scanf("%d %d", &start_node, &end_node);
    
    // 2. 초기화
    // 방문하지 않은 정점들을 1로 초기화 합니다.
    for (int i = 0; i < max_int; i++) check[i] = -1;
    
    // 3. 탐색
    bfs();
    
    // 4. 출력
    printf("%d\n", check[end_node]);
}