퍼셉트론이 왜 XOR 문제를 못푸는지 알아보기

skyepodium·2021년 5월 19일

퍼셉트론이 XOR 문제를 못푸는 이유를 알아보고, 다층 퍼셉트론으로 해결해봅시다.

1. 소개

인공지능의 역사에서 단층 퍼셉트론은 1957년 프랑크 로젠블라트에 의해 개발되었습니다.

하지만, xor 문제를 못푼다는 이유로, 긴 시간동안 암흑기를 가졌습니다.

2. 퍼셉트론

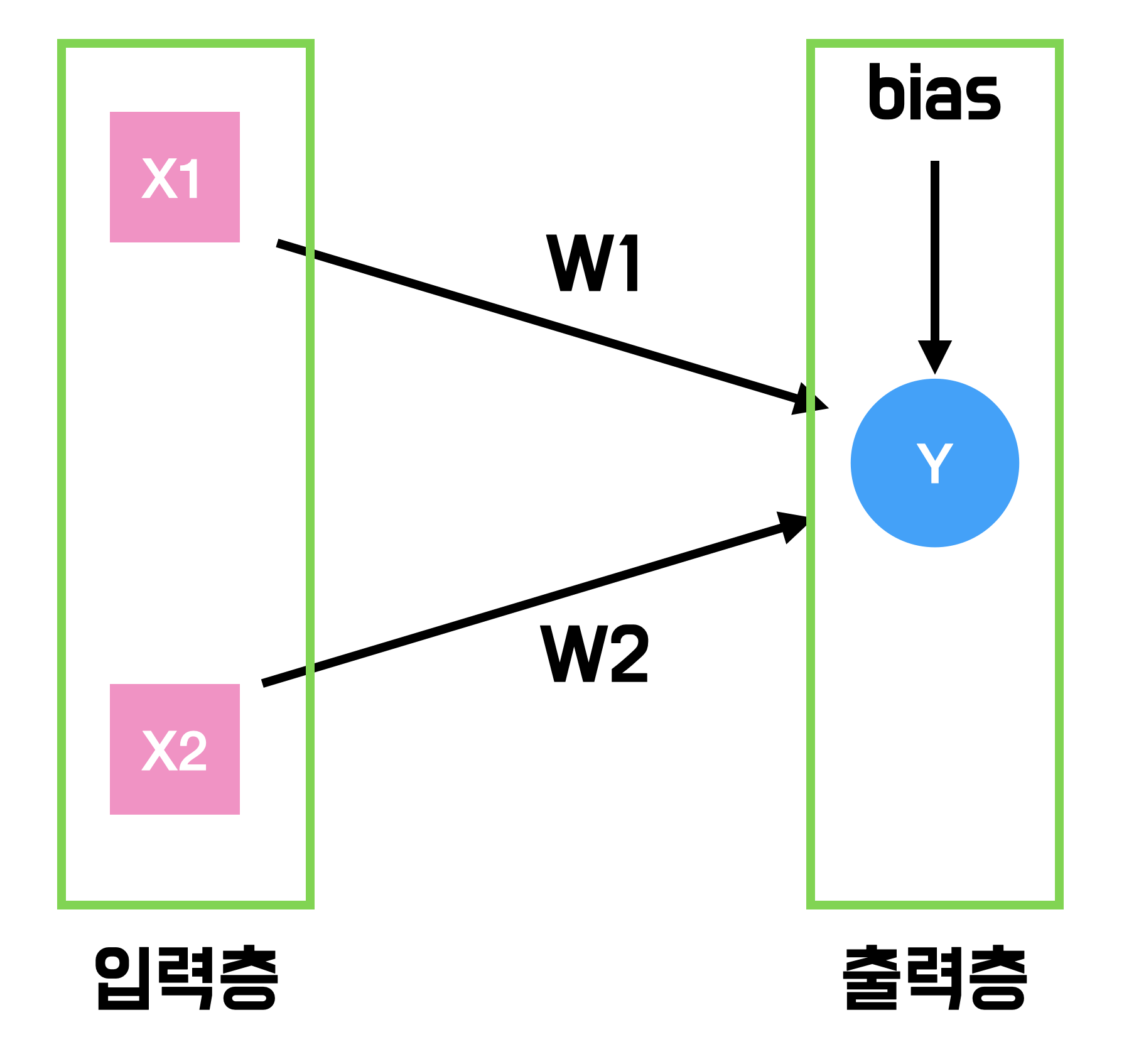
단층 퍼셉트론은 입력값에 대한 가중치와 편향을 계산해서 결과를 반환합니다.

3. OR gate

1) 구현

# or gate
def or_gate(x1, x2):
    # 입력값 x1에 대한 가중치 w1, x2에 대한 가중치 w2
    w1, w2 = 0.6, 0.6

    # bias 편향값
    b = -0.5

    # 연산 결과
    result = x1*w1 + x2*w2 + b

    # 결과가 0보다 작거나 같으면 0, 0보다 크면 1을 반환합니다.
    return 0 if result <= 0 else 1

    
    
# 입력값 목록을 튜플 리스트로 만듭니다.
input_list = [(0, 0), (0, 1), (1, 0), (1, 1)]


# 반복문을 순회하면서 입력값을 가져옵니다.
for x1, x2 in input_list:

    # or gate의 결과를 저장하고
    or_result = or_gate(x1, x2)

    # 출력합니다.
    print(f"입력값: {x1} {x2} / 결과: {or_result}")    
"""
입력값: 0 0 / 결과: 0
입력값: 0 1 / 결과: 1
입력값: 1 0 / 결과: 1
입력값: 1 1 / 결과: 1
"""

2) 시각화

x + y가 0.5 보다 작으면 0이라고 판단했기 때문에 1차 함수로 표현되고

2차원 평면에서 선 하나로 구분하는것과 같습니다.

    # bias 편향값
    b = -0.5

    # 연산 결과
    result = x1*w1 + x2*w2 + b

    # 결과가 0보다 작거나 같으면 0, 0보다 크면 1을 반환합니다.
    return 0 if result <= 0 else 1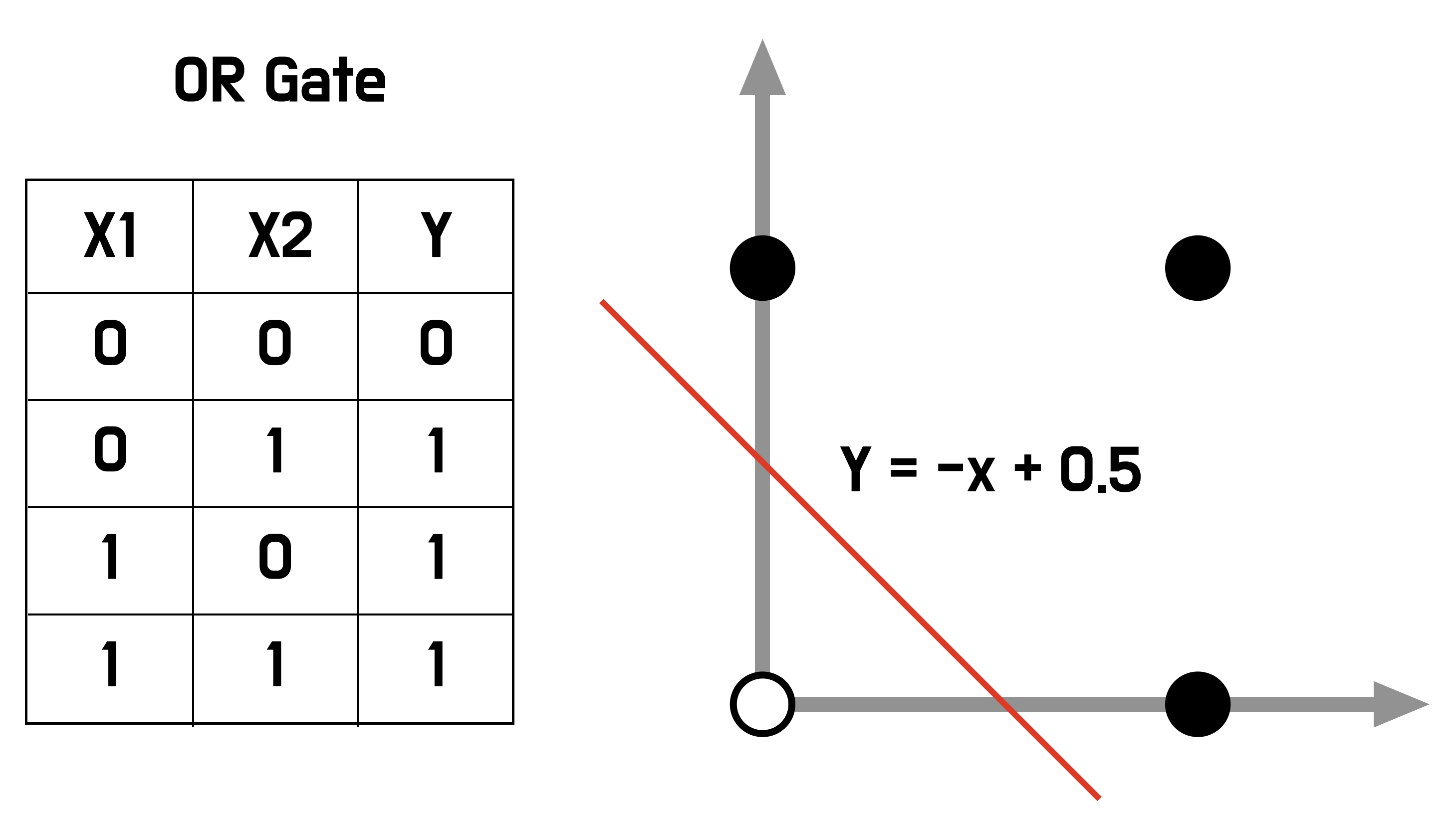

4. AND gate

1) 구현

# and gate
def and_gate(x1, x2):
    # 입력값 x1에 대한 가중치 w1, x2에 대한 가중치 w2
    w1, w2 = 0.6, 0.6

    # bias 편향값
    b = -0.7

    # 연산 결과
    result = x1*w1 + x2*w2 + b

    # 결과가 0보다 작거나 같으면 0, 0보다 크면 1을 반환합니다.
    return 0 if result <= 0 else 1

    
    
# 입력값 목록을 튜플 리스트로 만듭니다.
input_list = [(0, 0), (0, 1), (1, 0), (1, 1)]



# 반복문을 순회하면서 입력값을 가져옵니다.
for x1, x2 in input_list:
    # and gate의 결과를 저장하고
    and_result = and_gate(x1, x2)

    # 출력합니다.
    print(f"입력값: {x1} {x2} / 결과: {and_result}")
    
"""
입력값: 0 0 / 결과: 0
입력값: 0 1 / 결과: 0
입력값: 1 0 / 결과: 0
입력값: 1 1 / 결과: 1
"""

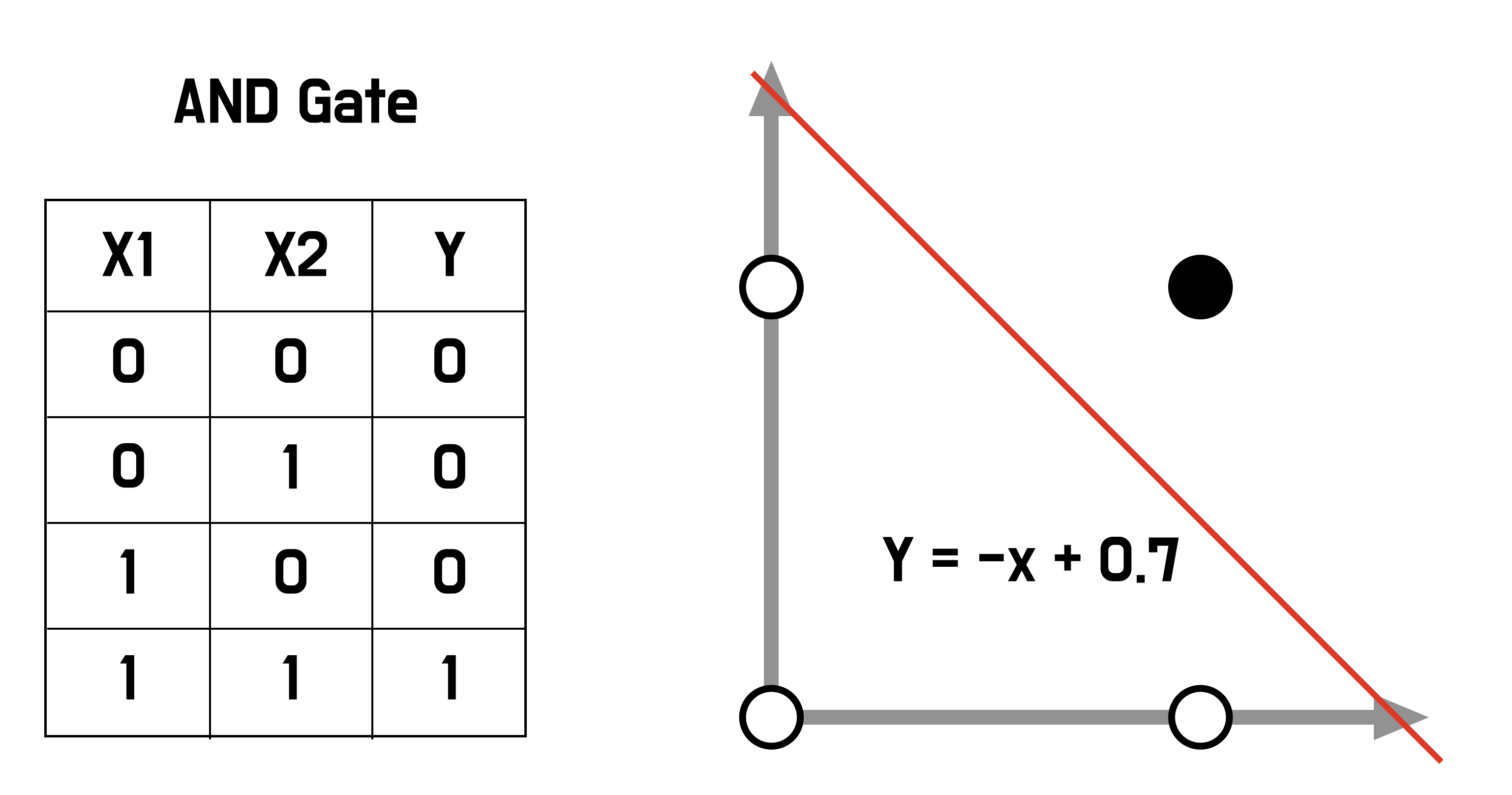
2) 시각화

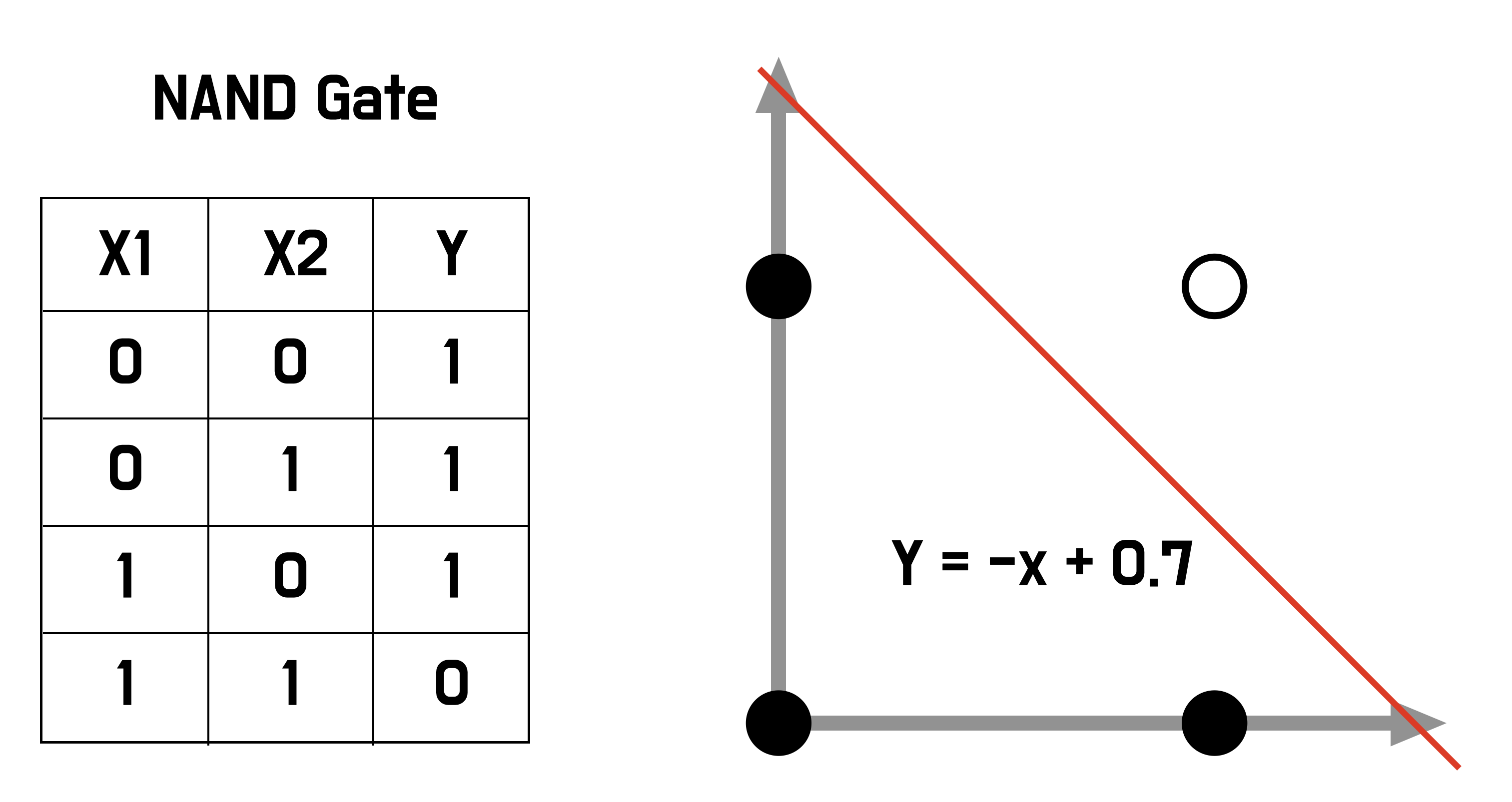
x + y가 0.7 보다 작으면 0이라고 판단했기 때문에 1차 함수로 표현되고

2차원 평면에서 선 하나로 구분하는것과 같습니다.

5. NAND gate

1) 구현

def nand_gate(x1, x2):
    # 입력값 x1에 대한 가중치 w1, x2에 대한 가중치 w2
    w1, w2 = 0.6, 0.6

    # bias 편향값
    b = -0.7
    # 연산 결과
    result = x1*w1 + x2*w2 + b

    # 결과가 0보다 작거나 같으면 1, 0보다 크면 0을 반환합니다.
    return 1 if result <= 0 else 0
    


# 입력값 목록을 튜플 리스트로 만듭니다.
input_list = [(0, 0), (0, 1), (1, 0), (1, 1)]


# 반복문을 순회하면서 입력값을 가져옵니다.
for x1, x2 in input_list:
    # nand gate의 결과를 저장하고
    nand_result = nand_gate(x1, x2)

    # 출력합니다.
    print(f"입력값: {x1} {x2} / 결과: {nand_result}")
    
"""
입력값: 0 0 / 결과: 1
입력값: 0 1 / 결과: 1
입력값: 1 0 / 결과: 1
입력값: 1 1 / 결과: 0
"""

2) 시각화

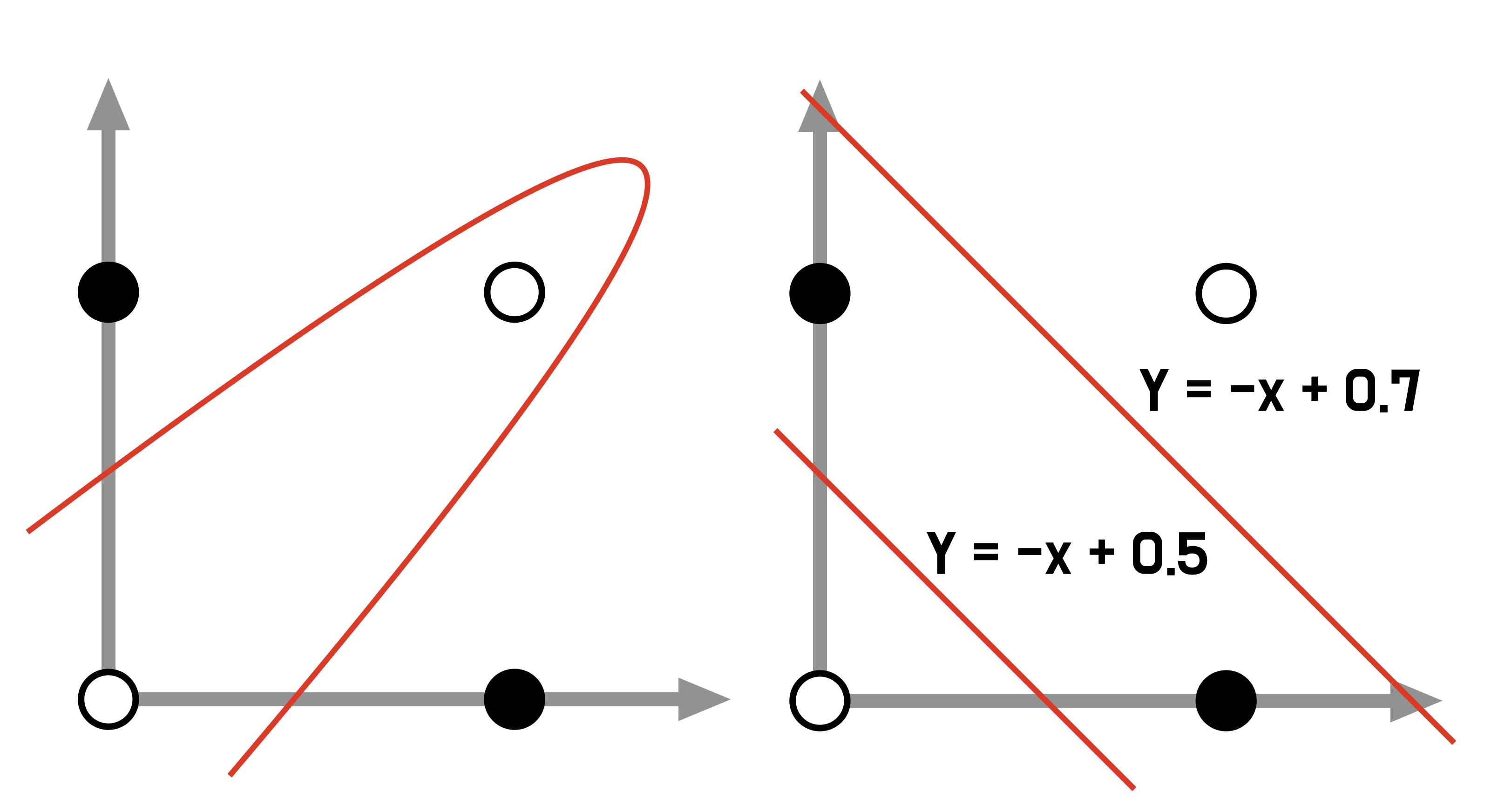
5. XOR Gate

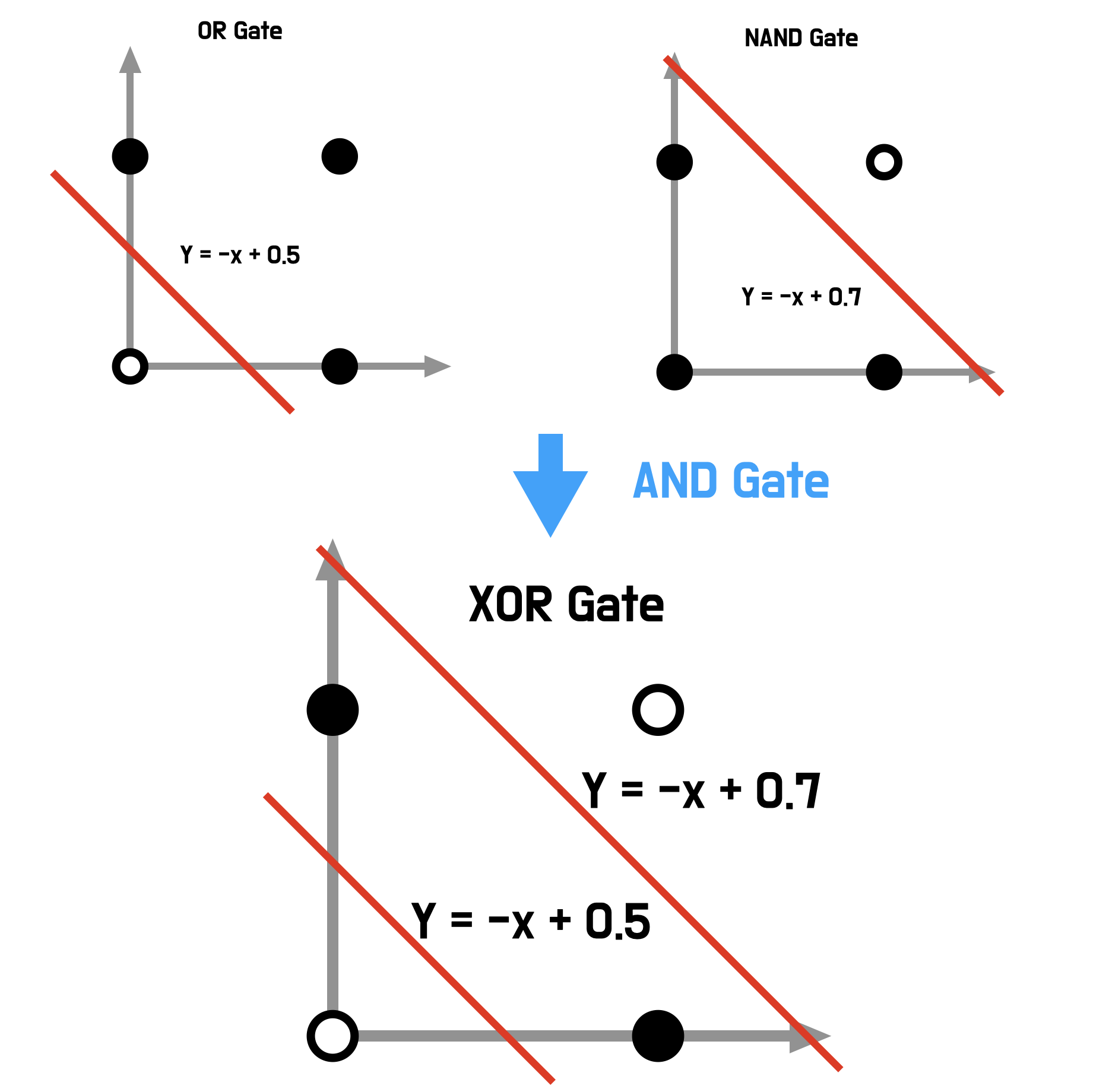
XOR 문제를 해결하려면 곡선을 그리거나, 2개의 직선을 그려야합니다.

하지만, 기존의 or, and, nand는 1개의 직선을 그리는 방식이고 이를 해결하지 못했습니다.

6. 다층 퍼셉트론

1) 소개

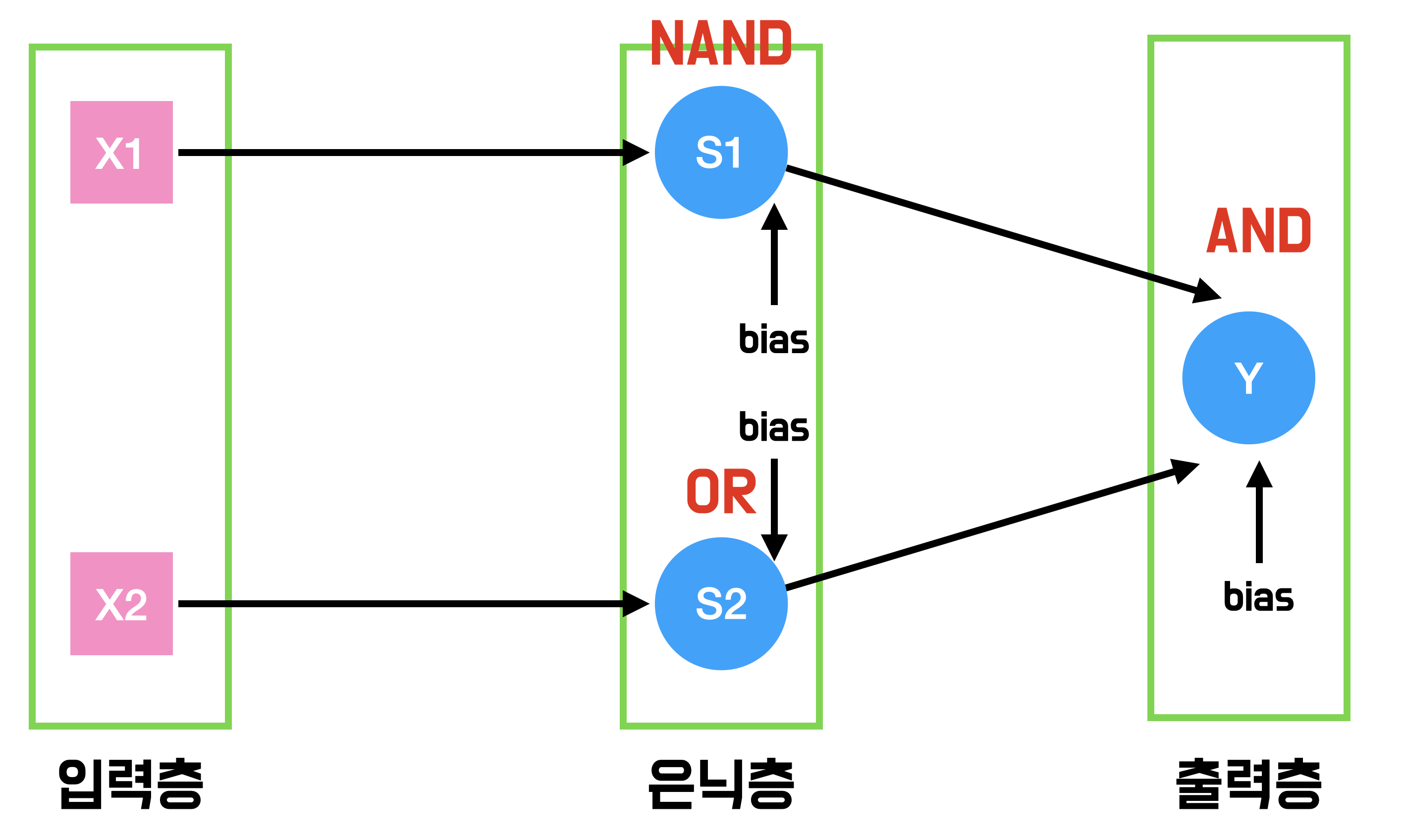
입력층과 출력층으로 구성된 단층 퍼셉트론에 은닉층이 추가되면 다층 퍼셉트론이라고 부릅니다. 은닉층은 기존의 출력층과 같이 가중치합을 계산합니다.

아래와 같이 3개의 논리 게이트 NAND, OR, AND 게이트를 조합하면 XOR 문제를 해결할 수 있습니다.

2) 구현

# and gate
def and_gate(x1, x2):
    # 입력값 x1에 대한 가중치 w1, x2에 대한 가중치 w2
    w1, w2 = 0.6, 0.6

    # bias 편향값
    b = -0.7

    # 연산 결과
    result = x1*w1 + x2*w2 + b

    # 결과가 0보다 작거나 같으면 0, 0보다 크면 1을 반환합니다.
    return 0 if result <= 0 else 1


# or gate
def or_gate(x1, x2):
    # 입력값 x1에 대한 가중치 w1, x2에 대한 가중치 w2
    w1, w2 = 0.6, 0.6

    # bias 편향값
    b = -0.5

    # 연산 결과
    result = x1*w1 + x2*w2 + b

    # 결과가 0보다 작거나 같으면 0, 0보다 크면 1을 반환합니다.
    return 0 if result <= 0 else 1


def nand_gate(x1, x2):
    # 입력값 x1에 대한 가중치 w1, x2에 대한 가중치 w2
    w1, w2 = 0.6, 0.6

    # bias 편향값
    b = -0.7
    # 연산 결과
    result = x1*w1 + x2*w2 + b

    # 결과가 0보다 작거나 같으면 1, 0보다 크면 0을 반환합니다.
    return 1 if result <= 0 else 0


# 입력값 목록을 튜플 리스트로 만듭니다.
input_list = [(0, 0), (0, 1), (1, 0), (1, 1)]


# 반복문을 순회하면서 입력값을 가져옵니다.
for x1, x2 in input_list:
    # or gate의 결과를 저장하고s
    or_result = or_gate(x1, x2)

    # nand gate의 결과를 저장하고
    nand_result = nand_gate(x1, x2)

    xor_result = and_gate(or_result, nand_result)

    # 출력합니다.
    print(f"입력값: {x1} {x2} / 결과: {xor_result}")
    
    
"""
입력값: 0 0 / 결과: 0
입력값: 0 1 / 결과: 1
입력값: 1 0 / 결과: 1
입력값: 1 1 / 결과: 0
"""