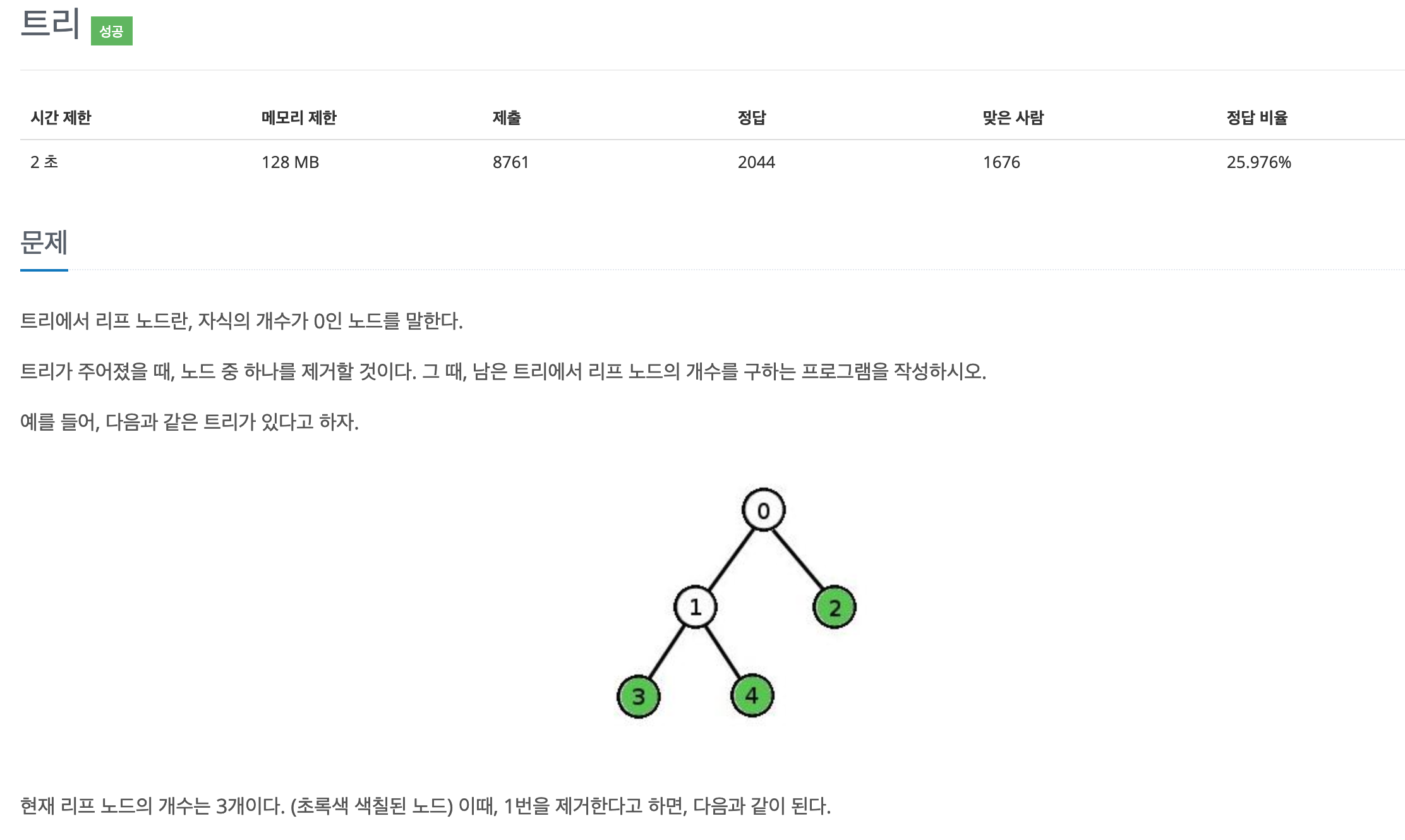
문제

• 첫재 줄에 n이 주어집니다. 정점의 개수가 n개인 트리이며, 트리의 정점은 0번부터 n-1까지 입니다.
• 둘째 줄에 각 정점의 부모 정점의 정보가 주어집니다. (-1이면 루트 노드 입니다.)
• 셋째 줄에 지울 노드 한개가 주어집니다.
• n(1 <= n <= 50) 정점의 수
• 시간 제한 2초
• 문제 링크

---

접근 과정

1. 탐색

• 사실 어려운 문제는 아닙니다. 1) 그래프를 구현하고, 2) BFS, DFS 아무거나 사용해서 탐색해주면 됩니다.
  단, 저는 루트 노드도 지울 수 있다는 점을 망각해서... 여러번 틀렸습니다.

2. 시간 복잡도 계산

• 1) 트리를 BFS로 탐색하는데 걸리는 시간은 log(V+E) V는 정점의 수, E는 간선의 수, 트리에서 E는 항상 V-1 이기 때문에 시간은 O(n), 상수생략
• n(1 <= n <= 50) 정점의 수 이기 때문에 O(n)은 O(50) 문제의 시간 제한이 2초 이기 때문에 시간안에 풀 수 있습니다.

코드

1. C++

#include <iostream>
#include <vector>
#include <queue>

#define max_int 51
using namespace std;

//시간 복잡도: O(n)
//공간 복잡도: O(n)
//사용한 알고리즘: BFS
//사용한 자료구조: 인접 리스트


int n, num, root_node, result = 0;
// 그래프를 저장할 인접 리스트
vector<int> v[max_int];

// 정점 방문 여부를 저장할 배열
bool check[max_int];

// BFS로 그래프를 탐색합니다.
void bfs(int start){
    check[start] = true;
    queue<int> q;
    q.push(start);

    while(!q.empty()){
        int node = q.front();
        q.pop();
        // 자식의 숫자를 계산할 변수
        int child_cnt = 0;
        for(int i=0; i<v[node].size(); i++){
            int next = v[node][i];
            if(!check[next]){
                child_cnt++;
                check[next] = true;
                q.push(next);
            }
        }
        // 자식이 없으면 단말 노드 계수를 1 증가 시킵니다.
        if(child_cnt == 0){
            result++;
        }
    }
}

int main(){
    // 1. 입력
    scanf("%d", &n);
    for(int i=0; i<n; i++){
        scanf("%d", &num);
        // 1) 인접 리스트를 사용해서 양방향 그래프로 트리를 만들어줍니다.
        if(num != -1){
            v[num].push_back(i);
            v[i].push_back(num);

        }
        // 2) 루트 노드일 경우 표시합니다.
        else {
            root_node = i;
        }
    }

    // 2. 지울 노드 표시
    scanf("%d", &num);
    check[num] = true;

    // 3. 만약 지워진 노드가 루트 노드가 아니라면 탐색을 시작합니다.
    if(!check[root_node]) bfs(root_node);

    // 4. 출력
    printf("%d\n", result);
}