직사각형의 넓이는 왜 가로×세로일까?

직사각형의 넓이는 다른 도형의 넓이를 구할 때 자주 사용되는 속성이다. 예를 들어 삼각형의 넓이는 (밑변×높이 / 2)인데, 이 것은 합동인 삼각형 두 개로 직사각형 하나를 만들 수 있다는 성질을 이용한 것이다. 그런데 왜 하필 직사각형의 넓이는 가로×세로일까? 넓이의 개념을 정확하게 이해하지 못하면 대답할 수 없는 질문이다.

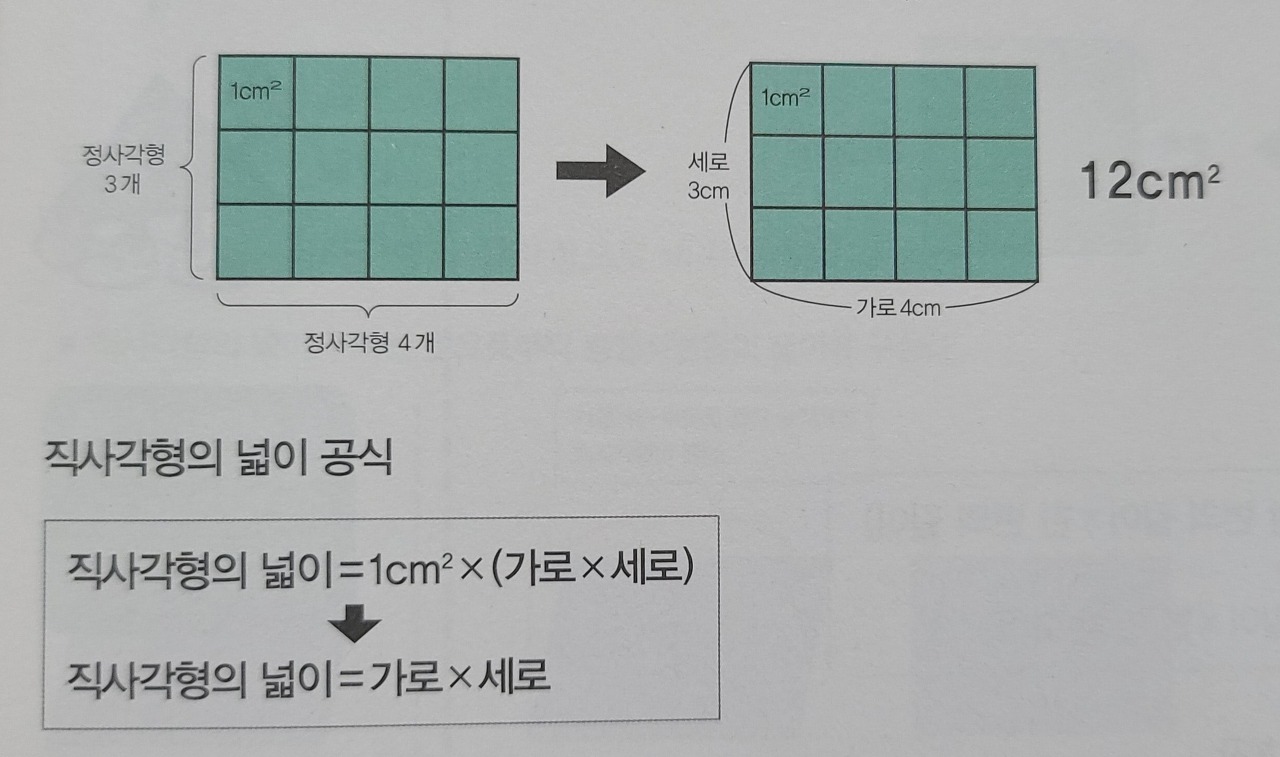
우리는 어떤 양을 나타내기 위해 단위라는 것을 사용한다. 단위란 다른 양을 표현하는 기준이 되는 양이다. 모든 양은 단위의 N배로 표현할 수 있다. 예를 들어 길이를 나타내는 단위는 미터(m)이다. 어떠한 길이가 1m의 100분의 1이면 1cm, 1000배면 km가 된다. 도형의 넓이를 나타날때는 한 변의 길이가 1인 '단위 정사각형'을 기준으로 삼는다. 어떤 도형의 넓이는, 그 도형 안에 포개놓을 수 있는 단위 정사각형의 개수로 표현한다.

이 개념을 이해했다면 직사각형의 넓이 공식은 쉽게 유도할 수 있다. 어떤 직사각형의 가로 길이가 N, 세로 길이가 M이라면 단위 정사각형을 가로로 N개, 세로로 M개 포개놓을 수 있다. 직사각형을 덮은 단위 정사각형의 개수는 N×M이다.

이미지 출처: https://brunch.co.kr/@kimnaya/13