Sorting Algorithms

where sorting algorithms help us?

---

• 사람들을 정렬할 때 - Sorting a list of people
• 중간값을 찾을 때 - Find the median
• 중복을 제거할 때 - Find duplicates in some date
• 이진탐색

왜 공부하는가?

---

• 정렬에 따른 성능의 차이 - 성능제약에 맞추기 위해서다.
• 큰 자료나 적은 자료냐 상황에 따라서 달라질 수 있다.

차이를 비교하고 이해해야 한다.

What does "stable" mean?

---

• 상대적인 그 위치를 최종결과에서 유지 되는가 ?
  • 같은 값이 있을때 처음의 상대적 위치가 정렬된 순서랑 같이 위치하여 있는가
• bubble sort, insertion sort, merge sort (selection sort 빼고)

What does "in place" mean?

---

bubble sort, insertion sort, selection sort (merge sort 빼고)

Bubble Sort

---

점진적으로 본인의 위치를 찾아간다. 위로 뽀글뽀글 🧼

1. 리스트가 있다.
2. 왼쪽에서 오른쪽으로 순회한다.
3. 이동하면서 왼쪽과 오른쪽을 비교한다.
4. 왼쪽이 더 크다면 왼쪽과 오른쪽을 바꾼다.
5. 오른쪽 끝까지 이동했다면 가장 큰 숫자가 제일 먼저 픽스 된다.

반복 순회하면서 왼쪽과 오른쪽을 바꿔간다.

length - 1 만큼 순회한다. 그치만 장담할 수 없다.

Big O

Time Complexity			Space Complexity
Average	Best	Worst	Worst
O(n^2)	O(n)	O(n^2)	O(1)

(셀병합도 html도 먹히지 않는다.. 😢)

Average, Worth O(n^2): 왼쪽에서 오른쪽으로 순회 하면서 총 횟수는 n번이다.
n번 순회가 끝나기전에 sorting이 완료 되었다 하여도 한번도 순회를 해야 순회를 끝내야하는지를 파악한다.

장점

• Memory: "in place" algorithm
  • In place - 리스트가 주어짐, 추가적인 다른 공간에 저장된 후 사용되는게 아니다. 추가적인 장소가 필요없다.
• stable
• 쉬운로직이다.
• 어떤리스트가 정렬이 되어있는지 안되어있는지 알 수 있다.

단점

• 성능적으로 별로다 - 자료가 많은 경우

javascript 구현

function bubbleSort (arr) {
  for (let i = 0; i < arr.length; i++) {
    let isSwap = false;

    for (let j = 1; j < arr.length; j++) {
      if (arr[j - 1] > arr[j]) {
        [arr[j], arr[j - 1]] = [arr[j - 1], arr[j]];
        isSwap = true;
      }
    }
    if (!isSwap) return arr;
  }
  return arr;
}

console.log(bubbleSort([2,4,6,1,2,5]));

isSwap으로 Best케이스일때의 O(n)을 구현
[arr[j], arr[j - 1]] = [arr[j - 1], arr[j]]; es6 Destructuring Assignment 사용

Insertion Sort

---

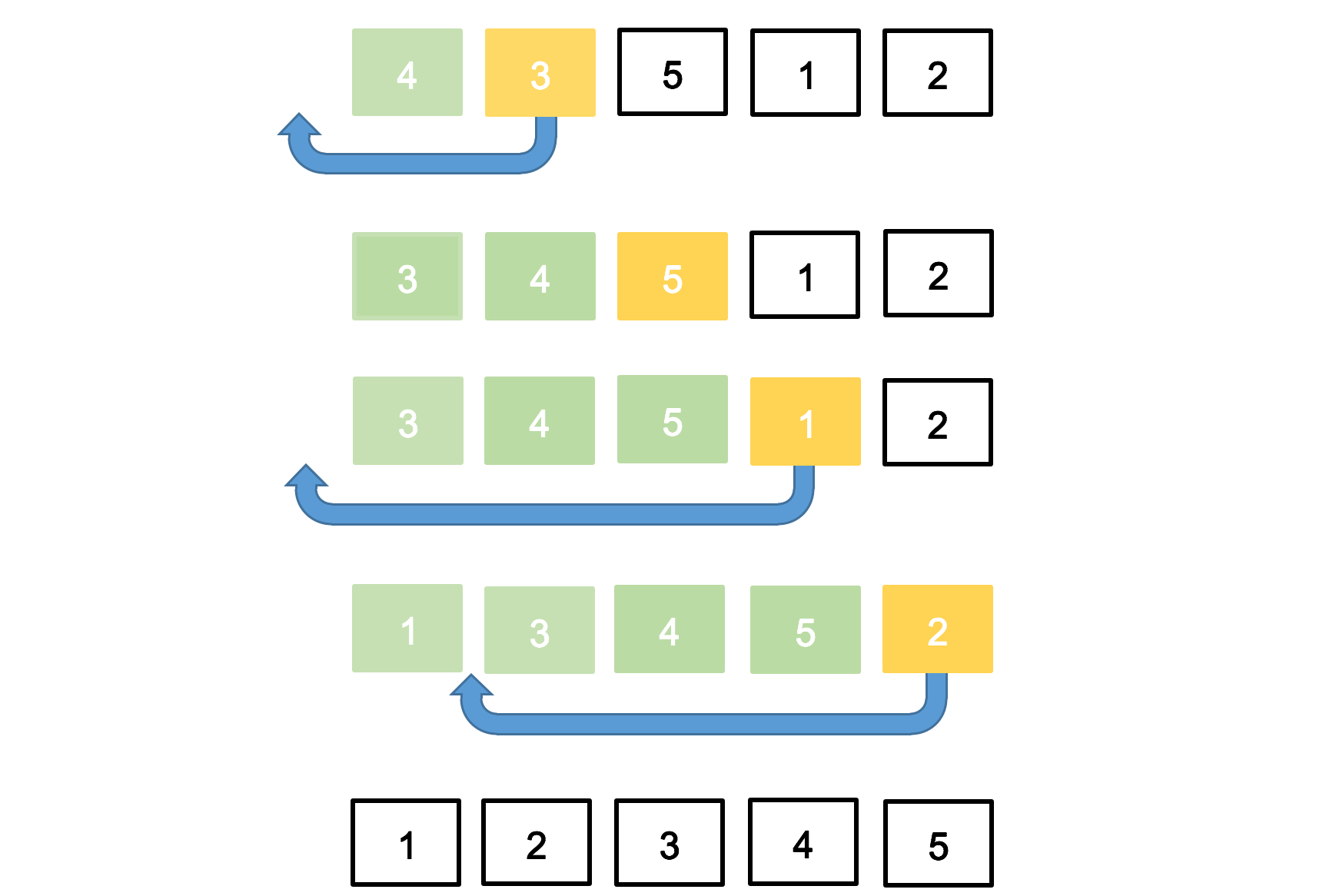
• index 1부터 비교를 시작하며 비교는 index - 1 이하로 위치한 요소(쉽게 말해 왼쪽 요소)와 비교한다.
• index - 1 이하 위치한 영역에서 자신의 상대적 위치를 찾아나간다.

Big O

Time Complexity			Space Complexity
Average	Best	Worst	Worst
O(n^2)	O(n)	O(n^2)	O(1)

장점

• In place
• stable

단점

• 성능적으로 별로다.

function insertionSort(arr) {
  for (let i = 1; i < arr.length; i++) {
    let key = arr[i];
    let j;

    for (j = i - 1; j >= 0 && arr[j] > key; j--) {
      arr[j+1] = arr[j];
    }
    arr[j+1] = key;
  }
  return arr;
}

console.log(insertionSort([1,5,6,2,6,7]));

Selection Sort

---

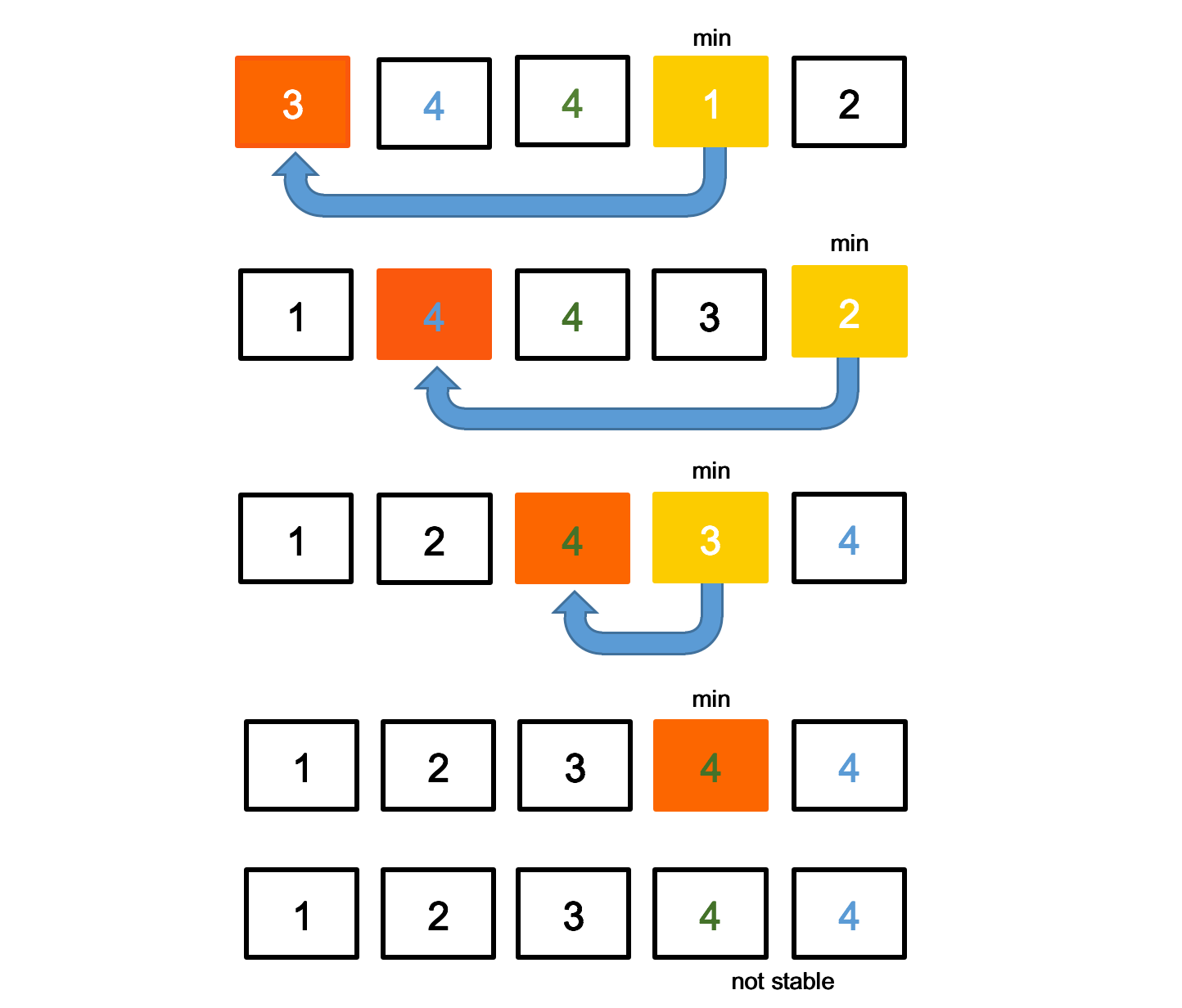
왼쪽 -> 오른쪽까지 순회한다.
가장 작은 수를 찾는 순회이다.

자리를 기준으로 정렬한다.

• 0번째 인덱스에 있어야 하는 수를 찾는다. (가장 작은 수)
• 1번째 인덱스를 찾는다. (두번째로 작은 수)
• 2번째 인덱스를 찾는다. (세번째로 작은 수)

Big O

Time Complexity			Space Complexity
Average	Best	Worst	Worst
O(n^2)	O(n^2)	O(n^2)	O(1)

• 시간 복잡도는 전부 Best와 Worst가 차이가 없다. 오직 절대적 위치를 찾기 위해 전체를 n번 돌기 때문이다.

Stable 하지 않는다.

• 상단 그림을 본다면 처음 파란색 4와 초록색 4가 있다. 마지막 최종에선 두 자리가 바뀌었다. 절대적 위치만 찾아가기 때문이다.

장점

• In place이다.

단점

• 퍼포먼스가 최악이다.

javascript로 구현하기

function selectionSort (arr) {
  for (let i = 0; i < arr.length - 1; i++) {
    let min = i;
    for (let j = i + 1; j < arr.length; j++) {
      if(arr[min] > arr[j]) min = j;
    }
    if(min !== i) [arr[min], arr[i]] = [arr[i], arr[min]];
  }
  return arr;
}

console.log(selectionSort([5,3,7,4,1,7]));

Quick Sort

1. 범위를 잡는다.
2. 기준이 되는 원소(pivot)를 선택한다.
   • 첫번째 원소
   • 중간 원소
   • 랜덤 원소
   • 마지막 원소
3. 범위 내에서 pivot보다 작은 수와 큰 수를 정렬한다.
4. pivot은 중간으로 위치한다.
5. 모두 정렬될 때까지 반복된다.

Big O

Time Complexity			Space Complexity
Average	Best	Worst	Worst
O(nlog(n))	O(nlog(n))	O(n^2)	O(log(n))

Best: 항상 중간값을 계속 pivot으로 선택할 때가 best case다.
Worst: 최악의 경우는 항상 최대, 최소의 pivot을 선택 할 때이다.

stable하고 in place다

javascript로 구현하기 (범위의 첫번째 원소가 pivot이다)

function quickSort(arr, pivotIndex, endIndex) {
  let storeIndex = pivotIndex + 1;

  for(let i = storeIndex; i <= endIndex; i++) {
    if(arr[i] < arr[pivotIndex]) {
      if(storeIndex !== i) {
        [arr[storeIndex], arr[i]] = [arr[i], arr[storeIndex]];
      }
      storeIndex += 1;
    }
  }

  if(storeIndex -1 !== pivotIndex) {
    [arr[pivotIndex], arr[storeIndex - 1]] = [arr[storeIndex - 1], arr[pivotIndex]];
  }

  if(pivotIndex < storeIndex - 2) quickSort(arr, pivotIndex, storeIndex - 2);
  if(storeIndex < endIndex) quickSort(arr, storeIndex, endIndex);

  return arr;
}

console.log(quickSort([5,4,8,6,1,8], 0, 5));

Merge Sort

---

이미지 출처

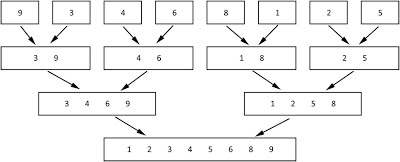
합쳐나가는 sorting 이다.

• 개별적으로 자른다.
• 두개를 비교한다. 비교 후 정렬한 후 통합한다.
• 두개 + 두개를 합칠때 맨앞에 자리를 두개 비교 뒷자리 두개를 비교한다.
• 네개 + 네개를 합칠때는 자리수로 또 비교한다.

Big O

Time Complexity			Space Complexity
Average	Best	Worst	Worst
O(nlog(n))	O(nlog(n))	O(nlog(n))	O(n)

Average, Best, Worst: 최대한 세세하게 나눈후 합쳐가는 뒤집어진 트리와 유사하다. 그래서 logn인데 여기다 원소의 갯수를 총 곱해서 n(logn)이다.

장점

• 평균적으로 보장이 되어있다.
• 자료가 많을 때 사용하기 좋다.
• stable 하다.

단점

• 한개가 하나의 배열이다. - in place로 할 수 없다. 공간적인 필요도가 o(n)
• 자료가 적을 때는 별로다.

Divide and Conquer

---

• Divide: 최대한 세세하게 작은 문제로 쪼갠다.
• Conquer: 재귀적으로 정렬한다.
• Combine
• Quicksort
• BST가 해당된다.

Divide and Conquer Algorithm Link

추가 알아볼 사항

• Dynamic Programming