세그먼트 트리

• 여러 개의 데이터가 존재할 경우 구간의 합을 구하는데 사용하는 자료구조
• 트리 종류 중에 하나이고 이진 트리의 형태이며 특정 구간의 합을 가장 빠르게 구할 수 있다. O(logN)

참고 사항 파이썬 배열 생성 시간 비교

import time
start = time.time()  # 시작 시간 저장
print('-------')
print('arr = [0 for i in range(n)] 시간')
for i in range(100):
    arr= [0 for i in range(1000000)]
print("time :", time.time() - start)  # 현재시각 - 시작시간 = 실행 시간
print('-------')
start = time.time()  # 시작 시간 저장
print('arr = [0] * 1000000 시간')
for i in range(100):
    arr= [0] * 1000000
print("time :", time.time() - start)  # 현재시각 - 시작시간 = 실행 시간

반복문으로 배열 생성과
[0] X n 으로 시간 차이가 궁금해서 한번 비교를 해보았는데

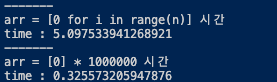
시간 비교를 해보니 10배 이상 차이가 난다..
배열 초기화를 할 경우에는 [0] X N 으로 하자!!

구현 과정

arr = [1,2,3,4,5,6,7,8,9,10]
tree = [0] * (len(arr) *4)

tree 의 크기를 할당 할때에는 배열의 개수가 N 일때는 N보다 큰 가장 가까운 N의 제곱수를 구할 뒤 그것의 2배를 하여 세그먼트 트리의 크기를 만들어야 한다
편하게 구하기 위해서 N에 4를 곱한 크기만큼 생성을 해두면 편하다.
이미지 참고

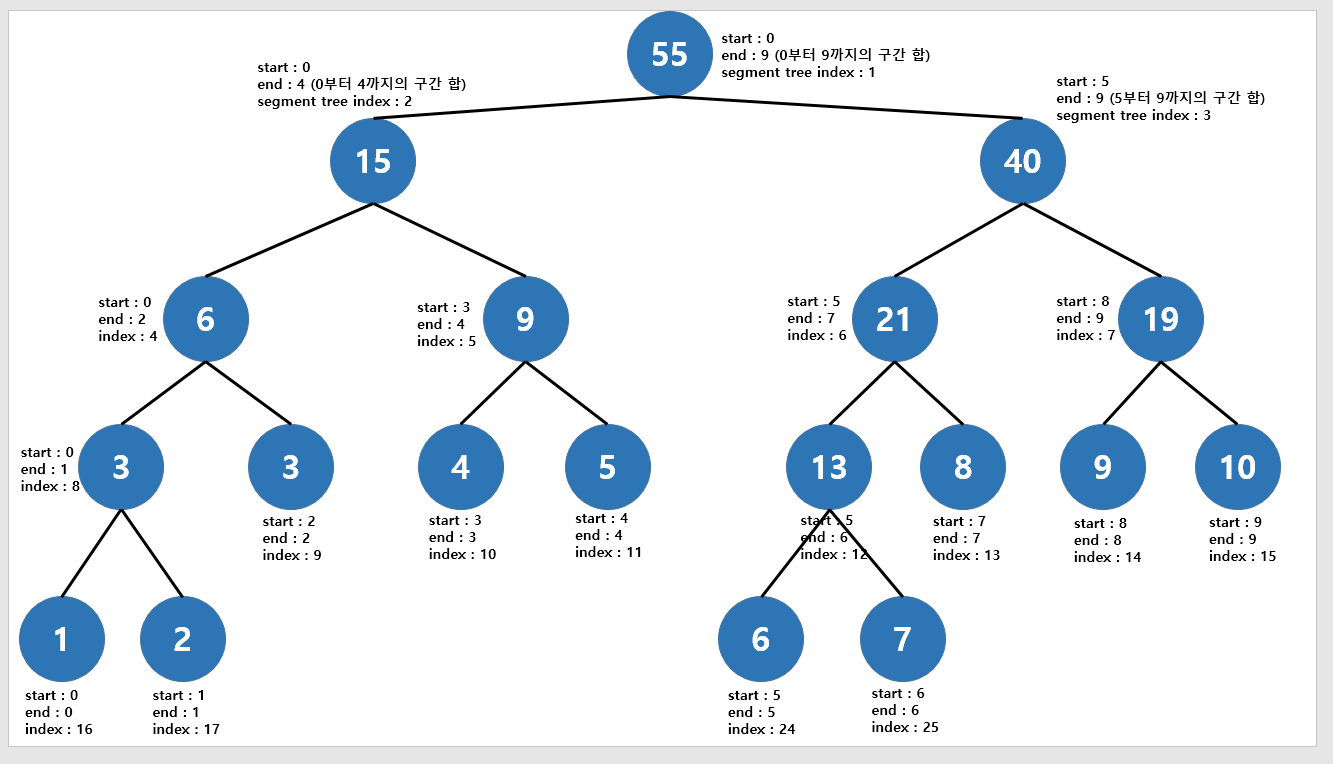
이런식으로 배열이 초기화가 된다.

# 세그먼트 트리의 초기화
# start : 배열의 시작 index , end : 배열의 마지막 index
# 시작 node는 1부터 시작
def init(node,start,end):
	if start==end:
    	tree[node] = arr[start]
        return tree[node]
	mid = (start+end) //2
    tree[index] = init(node*2,start,mid) + init(node*2+1,mid+1,end)
    return tree[index]

구간 합을 구하는 함수

원하고자 하는 구간에 들어왔을 경우에만 더해서 return 을 해주면 된다

# left , right : 구간 합을 구하고자 하는 범위
def subsum(node,start,end,left,right):
	# 범위 밖에 있는 경우
    if left > end or right < start:
    	return 0
	# 범위안에 들어갈 경우
    if left <= start and right >= end:
    	return tree[node]
	# 범위를 나눠서 더해줌
    mid = (start+end)//2
    c_left = subsum(node*2,start,mid,left,right)
    c_right = subsum(node*2+1,mid+1,end,left,right)
    return c_left+c_right

특정 원소의 값을 수정하는 함수

# 범위안에 들어가면 변경하면 된다.
def update(node,start,end,left,right,index,value):
	if index < start or index > end:
    	return
	# 범위 안에 있으면 변경
	tree[node] += value
    if start==end:
    	return
	mid = (start+end) // 2
    update(node*2,start,mid,index,value)
    update(node*2,mid+1,end,index,value)