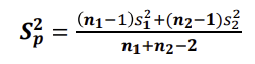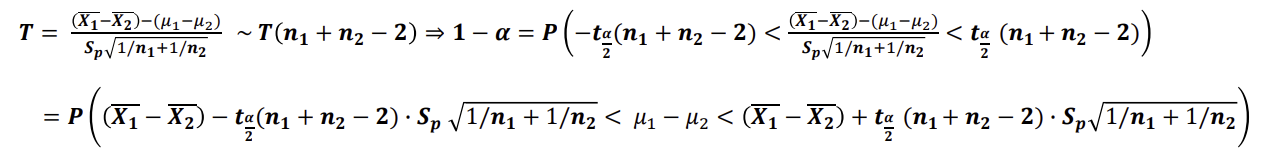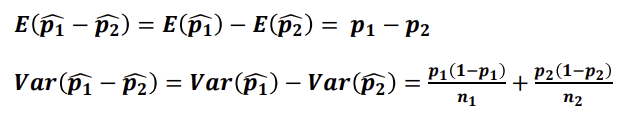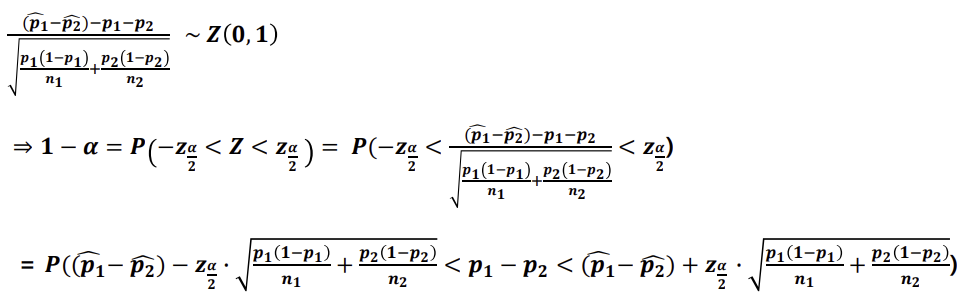1. 모집단(Population), 표본(Sample)
표본추출(Sampling)
- 모집단으로부터 표본을 추출 하는 것
- 표본에서 특성을 찾아내어 모집단의 특성을 추론하고자 함
- 복원추출(Sampling with replacement) : 데이터 하나를 추출하고 다시 넣어 추출하는 방법으로 동일한 표본이 추출될 수 있음
- 비복원추출(Sampling without replacement) : 데이터 하나를 추출하고 다시 넣지 않고 추출하는 방법
- Random Sampling : 각 개체를 모두 동일한 확률로 추출하는 방법(모집단에서 데이터를 추출할 때 편향되지 않도록 함)
불균형 데이터(Imbalanced Data) 문제
- 관심 있는 대상이 발생할 확률을 예측할 때, 예측 대상이 전체 대비 아주 낮다면 모델의 성능이 괜찮을까?
- 해결 방법 : Sampling 기법, 모델을 통한 성능 개선(Cost-sensitive learning)
- Sampling 기법
- 관심의 대상의 아주 비율이 낮은 경우
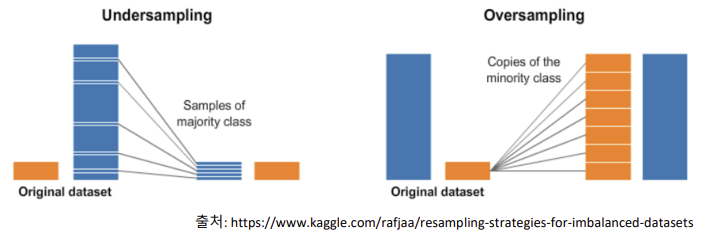
- Over Sampling : 타깃 데이터의 적은 class의 수를 많은 class의 비율만큼 증가시킴(일정 비율로 복원추출) ➡ 과도적합 문제 발생 가능
- Under Sampling : 타겟 데이터의 많은 class의 수를 적은 class의 비율만큼 감소시킴 ➡ 임의로 뽑은 데이터가 편향될 수 있고, 모형의 성능이 저하될 수 있음
표본평균(Sample Mean)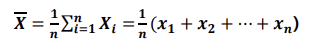
- 표본평균의 기대값
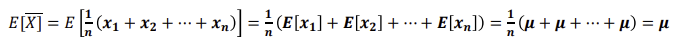
- 표본평균의 분산
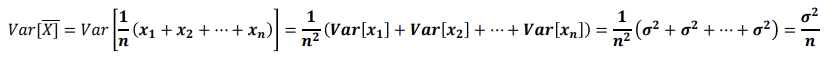
중심극한정리(Central Limit Theorem)
평균이 μ이고 분산이 σ²인 임의의 모집단에서 랜덤 표본 X1, X2, ... Xn을 추출할 때 표본의 크기 n이 충분히(n ≥ 30) 크면, 표본 평균은 근사적으로 정규분포를 따른다.
3. 표본분포(Sampling Distribution)
- 통계량(Statistic) : 표본에 기초하여 계산되는 수치 함수
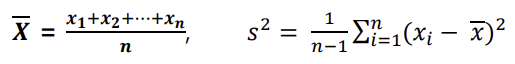
- 표본분포 : 통계량들이 이루는 분포
카이제곱분포(Chi-square distribution)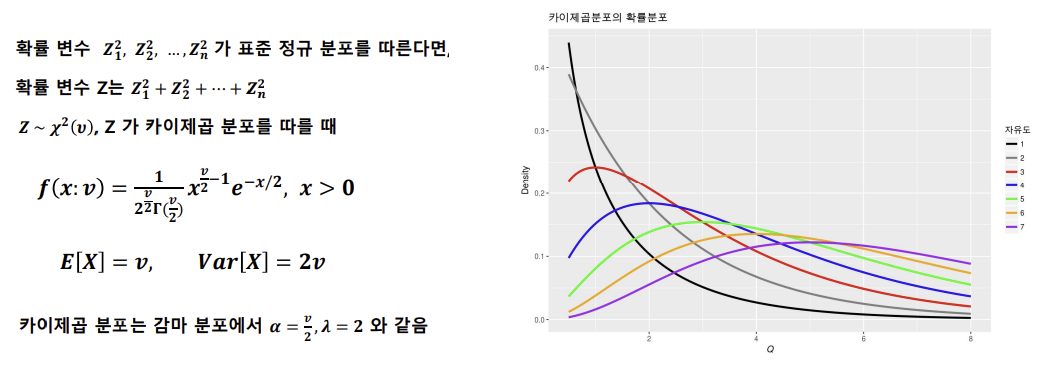
- 범주형 자료 분석에서 활용한다.
- 자유도(Degree of Freedom) : 표본수-제약조건의 수 또는 표본수-추정해야 하는 모수의 수를 의미하며 일반적으로 n-1을 사용한다.
- 예를 들어 표본 크기가 5, 표본 평균이 3일 때 숫자 4개는 자유롭게 정할 수 있으나, 마지막 하나의 숫자는 나머지 네 개의 숫자에 의해 결정된다. 1, 2, 3, 4를 선택했다면, 평균 3에 맞추기 위해 마지막 숫자는 자동으로 5가 된다.
- 자유도(v)가 클수록 카이제곱분포는 좌우 대칭 형태가 된다.
- 카이제곱분포는 자유도가 커지면서 표준정규 분포에 근사하며, v ≥ 30이면, 근사적으로 확률을 정규분포로 구할 수 있다.
t분포(t-distribution)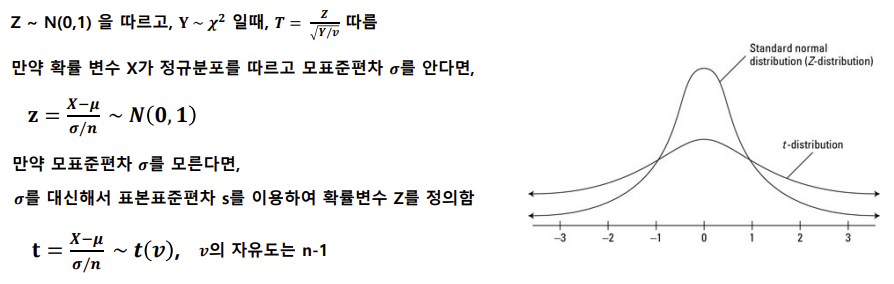
F분포(F-distribution)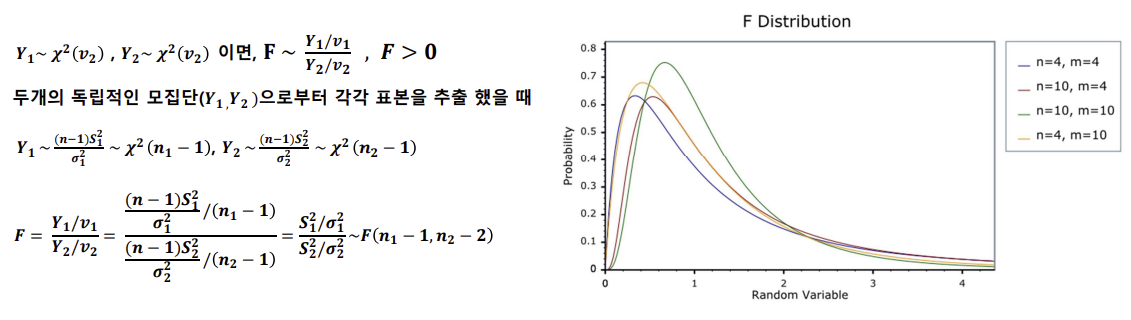
- 서로 독립인 두 정규모집단의 분산 또는 표준편차들의 비율에 대한 통계적 추론, 분산 분석 등에 활용된다.
4. 추정
- 추정(Estimation) : 모집단의 모수를 모를 때 표본으로 추출된 통계량을 모집단의 근사값으로 사용하는 것
- 추정량(Estimator) : 표본평균으로 모평균을 추정할 때 표본평균을 모평균에 대한 추정량이라고 함
점추정(Point Estimation)
-
모수를 하나의 특정값으로 추정
-
일치성(Consistency) : 표본의 크기가 모집단의 크기에 근접해야 함 ➡ 표본 크기가 클수록 추정량의 오차가 작아짐
-
불편성(Unbiased Estimator) : 추정량이 모수와 같아야 함
- 불편 추정량 : 모수가 θ, 추정량이 θ^ 일 때, E[θ^] = θ 일 때의 추정량
- E[θ^] = θ 가 아니라면 편의(biased) 있다고 함
-
유효성(Efficiency) : 추정량의 분산이 최소값이어야 함
- 모수에 대한 추정량의 분산이 작을수록 추정량이 효율적
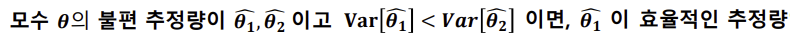
- 모수에 대한 추정량의 분산이 작을수록 추정량이 효율적
-
평균오차제곱(MSE, Mean Squared Error) : 평균오차제곱이 최소값이어야 함
구간추정(Interval Estimation)
- 모수가 포함될 수 있는 구간을 추정
- 신뢰구간(Confidence Level) : 추정값이 존재하는 구간에 모수가 포함될 확률
- 신뢰구간은 신뢰 하한, 신뢰 상한으로 표시함(추정하는 모수가 θ)
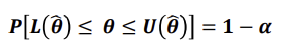
- 만약 모평균 μ를 추정한다면, 표본평균이 x이고 표준오차가 sd일 때 신뢰구간은
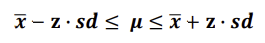
- 신뢰구간은 신뢰 하한, 신뢰 상한으로 표시함(추정하는 모수가 θ)
- 신뢰수준 : 100 * (1-a)% (a=오차 수준)
- 신뢰수준 95%라는 것은 구간 추정된 값의 오차가 발생할 확률이 5%라는 것
- 이때 오차를 유의수준(Significant Level)이라고 하며, p= 0.05라고 표현함
5. 모평균의 구간추정
- 모집단의 분산을 아는 경우

- 모집단의 분산을 모르는 경우

- 표본의 크기 결정
- 허용오차(Permissible Error) : 추정한 값이 틀려도 허용할 수 있는 오차
- 정규분포의 신뢰구간을 통해 허용오차를 계산함
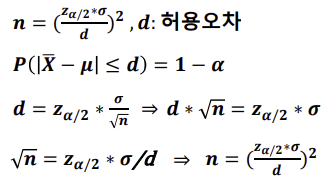
6. 모비율의 추정
모비율의 점추정
- 원하는 속성(class)에 속하면 ‘1’ 아니면 ‘0’일 때, 1의 속성을 갖는 것의 개수를 X라고 할 때 X ~ B(n,p) ➡ 이 때 모비율의 점추정량을 표본비율(sample proportion)이라고 함
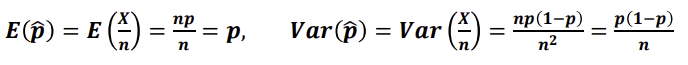
- 예) A대학에서 취업 성공한 학생의 비율은 몇 %? 표본을 통해서 전체 비율을 추정
모비율의 구간추정
- 모비율 구간추정에서 정규분포의 근사가 가능한 대표본은 보통 np>5, n(1-p)>5를 동시에 만족 해야함
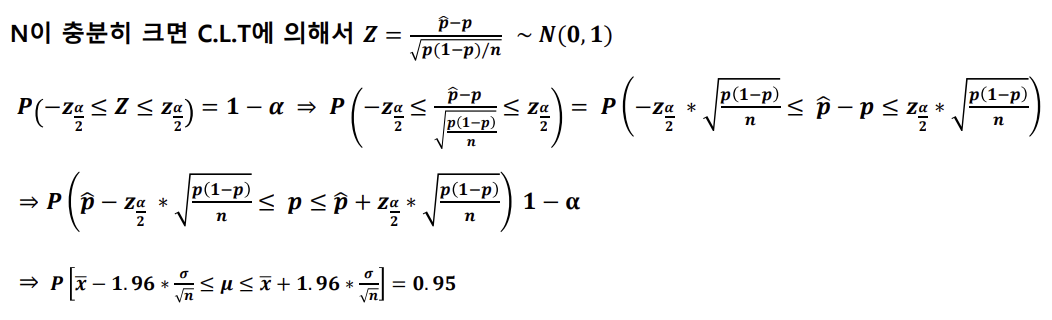
- 예) 20대의 A사 핸드폰 사용률을 알기 위해서 무작위로 500명을 대상을 조사한 결과 212명이 A사 핸드폰을 사용 중이었다. 20대 전체의 A사 핸드폰 사용률에 대한 추정값을 구하고 95% C.I를 구하면?

모비율의 표본크기
- 오차의 한계
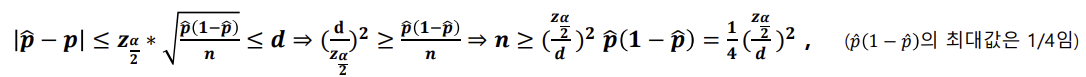
- 예) 20대의 A사 핸드폰 사용률을 추정에 대한 95% 신뢰구간으로 오차의 한계를 0.01로 하기 위한 표본의 크기는?
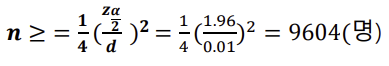
모평균 차이의 추정(점추정)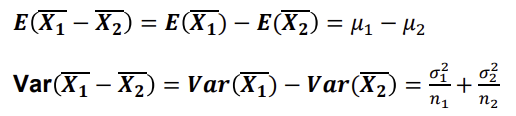
모평균 차이의 추정(구간추정-대표본)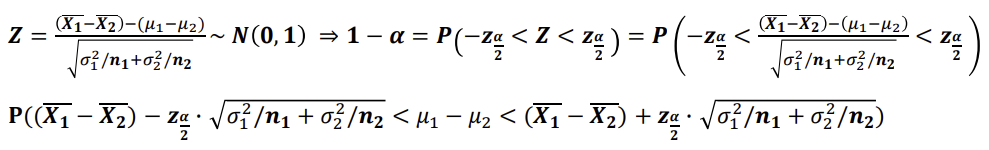
모평균 차이의 추정(구간추정-소표본, 모분산을 모를 때)
- 두 모집단의 분산을 안다면 대표본과 동일하게 추정 가능하나, 모른다면 등분산 가정이 필요함(두 모집단의 분산이 같다는 가정 σ² = σ²1 = σ²2)
- 합동 분산 추정량(Pooled Variance Estimator) : 공통 분산의 추정량