[프로그래머스] 위장 (Python3) | 조합? 경우의 수?

프로그래머스 해시 연습문제 중..
https://programmers.co.kr/learn/courses/30/lessons/42578

문제에서 '조합의 수'를 본 나는 조합을 활용하여 문제를 풀기 시작했다.

옷의 종류만큼 check라는 boolean 딕셔너리를 만들어주고, 입을 수 있는 옷의 모든 조합을 구하는 combi()라는 함수를 만들었다.

combi()함수는 값을 넣고 재귀 호출, 빼고 재귀호출을 반복하며 구한 조합의 틀을 활용하여 구현하였다.

이 포스트 참고

나의 첫번째 코드(조합)

def solution(clothes):
    global answer
    answer = 0
   
    all_kind = []
  
    for i,j in clothes: # 옷의 종류를 담은 리스트
        all_kind.append(j)
 
    check = {}
    for k in all_kind:
        check[k] = False

    def combi(n, ans):
        if n == len(clothes):
            global answer
            answer += 1
            return
           
        if check[clothes[n][1]] == False:
            ans.append(clothes[n][0])
            check[clothes[n][1]] = True
            combi(n+1, ans)
            ans.pop()
            check[clothes[n][1]] = False
            combi(n+1, ans)
        else:
            combi(n+1, ans)
          
    combi(0, [])
    return answer-1

하지만 결과는 시간초과...

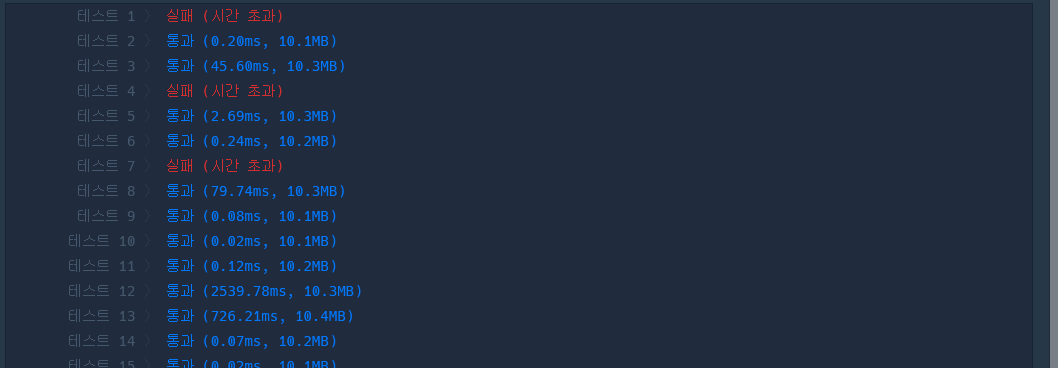
모든 조합을 만들어 푸는 문제가 아니었다.
.
.
.
.
.

문제로 다시 돌아가, 제한사항을 확인해 보았다.

제한사항

clothes의 각 행은 [의상의 이름, 의상의 종류]로 이루어져 있습니다.
스파이가 가진 의상의 수는 1개 이상 30개 이하입니다.
같은 이름을 가진 의상은 존재하지 않습니다.
clothes의 모든 원소는 문자열로 이루어져 있습니다.
모든 문자열의 길이는 1 이상 20 이하인 자연수이고 알파벳 소문자 또는 '_' 로만 이루어져 있습니다.
스파이는 하루에 최소 한 개의 의상은 입습니다.

의상의 최대 수는 30개, 즉 2^30 개의 경우의 수로 이는 대충 계산해봐도
2^10 x 2^10 x 2^10 = 1000^3 = 10억, 즉 10초가 넘는다.

예시
3개의 옷 종류를 입는 경우의 수

O O X
O X O
X O O
O O X
O X O
X O O
O O O
X X X (아무 것도 안 입는 경우)

=> 2^3

결국, 조합의 개수로 푸는 문제는 아니었다..

---

나의 두 번째 풀이

옷의 종류별로 경우의 수를 구하면 생각보다 간단하게 풀리는 문제였다.

예를 들어, A 종류의 옷이 3벌, B 옷의 종류의 옷이 2벌이라면 2x3 = 6 개의 경우의 수가 나온다.

하지만 이문제의 경우, A를 안 입는 경우, 그리고 B를 안 입는 경우를 추가하여야 하기 때문에 (3+1)*(2+1) 의 식을 도출할 수 있다.
또한, 최소 한 개의 의상은 입는다고 하였기에 아무 것도 안 입는 경우를 뺀 값을 정답으로 한다.

def solution(clothes):
    answer = 1
   
    dic = {}
  
    for i, j in clothes:
        if j in dic:
            dic[j] +=1
        else:
            dic[j] = 1
   
    for key in dic:
        answer *= dic[key]+1
   
    return answer-1