시간복잡도와 공간복잡도

시간 복잡도

시간 복잡도란 '문제를 해결하는 데 걸리는 시간과 입력의 함수 관계'를 가리킵니다. 어떠한 알고리즘의 로직이 '얼마나 오랜 시간'이 걸리는지를 나타내는 데 쓰이며, 보통 빅오 표기법으로 나타냅니다.

빅오 표기법

빅오 표기법이란 입력 범위 n을 기준으로 해서 로직이 몇 번 반복되는지 나타내는 것입니다.

예를 들어 '입력 크기 n'의 모든 입력에 대한 알고리즘에 필요한 시간이 10n^2+n이라고 한다면 다음과 같은 코드를 상상할 수 있습니다.

for (int i=0; i<10; i++) {
	for (int j=0; j<n; j++) {
    	for (int k=0; k<n; k++) {
        	if (true) cout << k <<'\n';
        }
    }
}
for (int i=0; i<n; i++) {
	if (true) cout << i << '\n';
}

위 코드의 시간 복잡도를 빅오 표기법으로 나타내면 O(n^2)이 됩니다.
'가장 영향을 많이 끼치는' 항의 상수 인자를 빼고 나머지 항을 없앤 것이죠. 입력의 크기가 커질수록 연산량이 가장 많이 커지는 항은 n의 제곱항이고, 다른 것은 그에 비해 미미하기 때문에 이것만 신경 쓰면 된다는 이론입니다.

시간 복잡도의 존재 이유

시간 복잡도는 왜 필요할까요? 바로 효율적인 코드로 개선하는 데 쓰이는 척도가 되기 때문입니다.

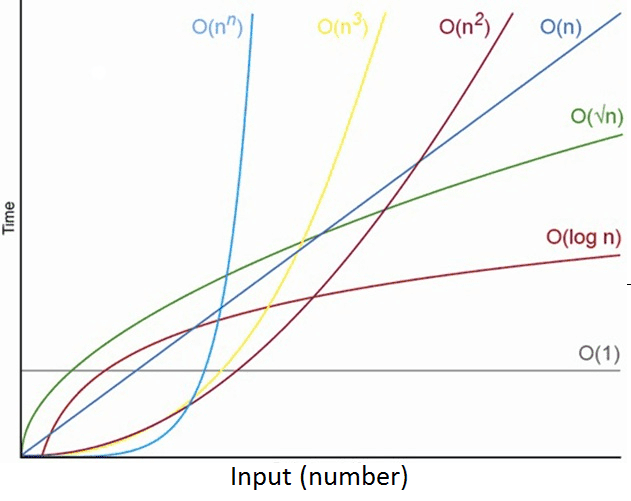
위 그림처럼 O(1)과 O(n)은 입력 크기가 커질수록 차이가 많이 나는 것을 볼 수 있습니다.

---

공간 복잡도

공간 복잡도는 프로그램을 실행시켰을 때 필요로 하는 자원 공간의 양을 말합니다. 정적 변수로 선언된 것 말고도 동적으로 재귀적인 함수로 인해 공간을 계속해서 필요로 할 경우도 포함입니다.

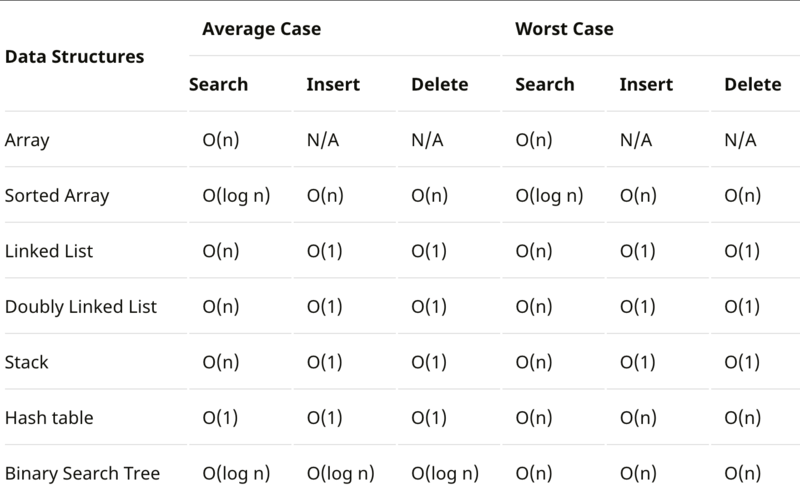
자료 구조에서의 시간 복잡도

자료 구조를 사용할 때는 이러한 시간 복잡도를 잘 생각해야 합니다.