백준 1309 동물원 (JAVA)

https://www.acmicpc.net/problem/1309

문제

실버 1 수준의 DP 문제이다
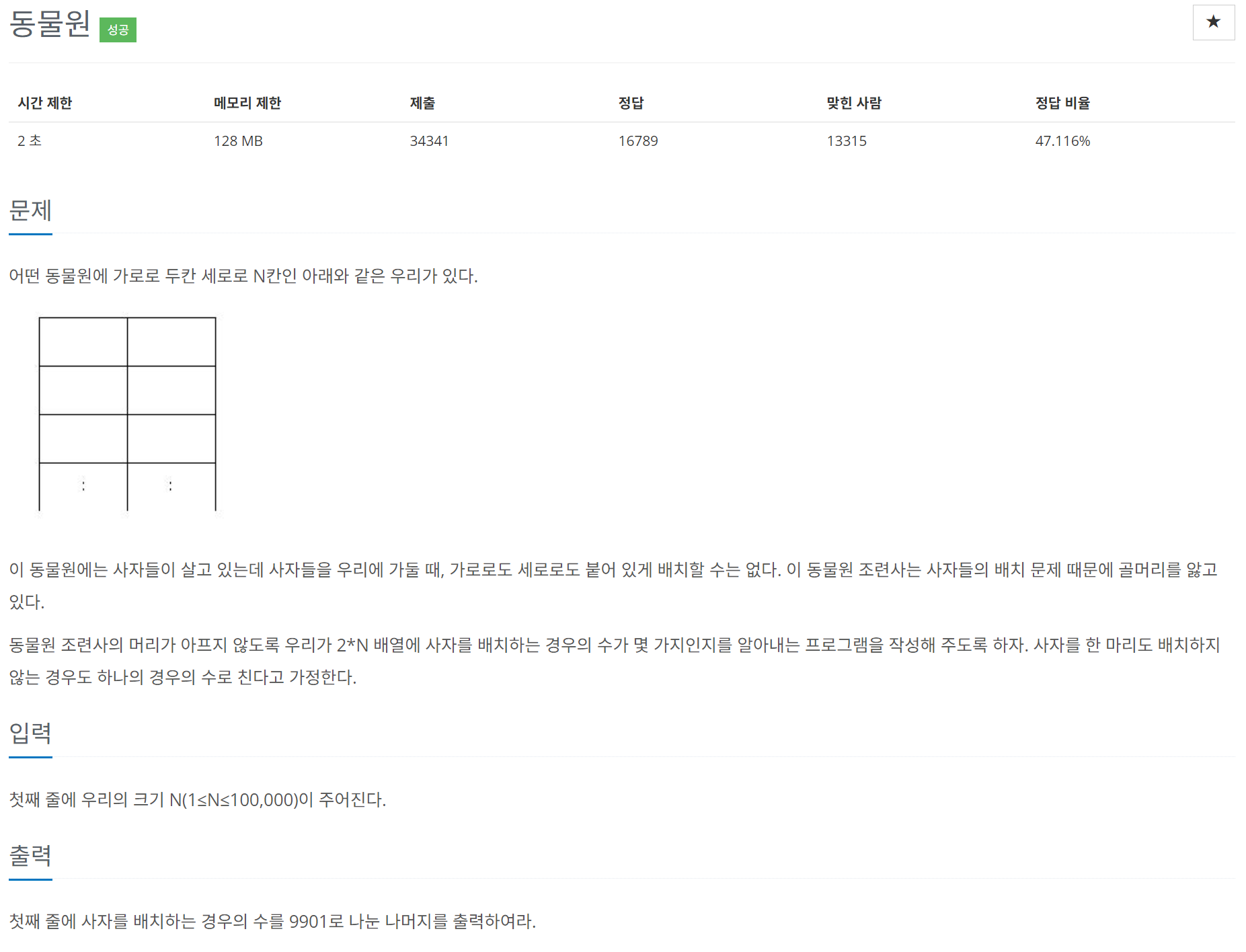
가로로 2칸, 세로로 N칸인 우리에 사자를 배치해야 하는데,
가로나 세로로 붙어 있게 배치할 수 없다.
그리고 사자도 0마리부터 최대 배치할 수 있는 마리수까지 모든 경우의 수를 합해야 한다.
이 부분은 문제에 설명이 제대로 안 되어 있어서 직접 계산해보는데 시간이 좀 걸렸다.

---

아이디어

DP를 2차원 배열로 설정하여 각 배열마다 사자가 있는 경우를 카운팅하여야 한다.
dp[i][j] = n : i번째 줄에서, j번째 칸에 동물을 놓을 수 있는 경우의 수 n 를 dp로 계산하여야 한다.
그리고, 해당하는 줄에 사자가 없을 수도 있기 때문에 사자가 해당 줄에 없는 경우도 설정해야 하기 때문에,

int [][] dp = new int [n+1][3]

으로 두번째 배열을 3으로 설정하여야 한다.

첫 줄은 Base Case로 다 값을 1로 설정하고,

다음 경우의 수의 따라서 점화식이 바뀐다

1) j가 0일경우 (해당 줄에 사자가 없을 경우)

dp[i][0] = dp[i-1][0] + dp[i-1][1] + dp[i-1][2]

2) j가 1일 경우 (해당 줄 첫번째 칸에 사자가 있을 경우)

dp[i][1] = dp[i-1][0] + dp[i-1][2]

3) j가 2일 경우 (해당 줄 첫번째 칸에 사자가 있을 경우)

dp[i][2] = dp[i-1][0] + dp[i-1][1]

---

코드

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);

        int n = sc.nextInt();
        int[][] dp = new int[n+1][3];

        dp[1][0] = 1;  // 아무칸에도 사자를 두지 않는 경우
        dp[1][1] = 1;  // 왼쪽칸에 사자를 두는 경우
        dp[1][2] = 1;  // 오른쪽칸에 사자를 두는 경우

        for (int i = 2; i < n + 1; i++) {
            // i번째에 사자를 아무칸에도 두지 않는 경우
            // = i-1번째 사자를 두지 않음 + i-1번째 왼쪽칸에 사자를 둠 + i-1번째 오른쪽 칸에 사자를 둠
            dp[i][0] = (dp[i - 1][0] + dp[i - 1][1] + dp[i - 1][2]) % 9901;

            // i번째에 사자를 왼쪽칸에도 두는 경우
            // = i-1 칸에 사자를 두지 않음 + i-1 오른쪽 칸에 사자를 둠
            dp[i][1] = (dp[i - 1][0] + dp[i - 1][2]) % 9901;

            // i번째에 사자를 오른쪽칸에도 두는 경우
            // = i-1 칸에 사자를 두지 않음 + i-1 왼쪽 칸에 사자를 둠
            dp[i][2] = (dp[i - 1][0] + dp[i - 1][1]) % 9901;
        }

        System.out.println((dp[n][0] + dp[n][1] + dp[n][2]) % 9901);
    }
}

---

느낀 점

DP가 익숙하지 않아서 시간도 많이 걸리고 chatGPT를 참고할 수 밖에 없었다
나중에 다시 한번 풀어보면 좋을만한 문제인거 같다