
Stack과 Queue에 대해 배우고 또 새로운 데이터 구조를 배웠다. 트리는 많이 본 모양이라서 익숙했는데, 그래프는 내가 생각하고 있던 그래프 형태와는 달라서 흠칫했다 ㅎ..
데이터 구조 파트에 오고나서부터 낯설고 생소해서 못하는건지 내가 그냥 이해를 잘 못하는건지 ㅠㅠ.... 전자라고 생각해야지...
일단 배운 내용을 정리하며 개념에 대해 다시 생각해봐야겠다. ( 코플릿 문제 접근부터 힘들었기때문...😖)
1. Graph
여러개의 점들이 서로 복잡하게 연결되어 있는 관계를 표현한 자료구조
컴퓨터 공학에서 말하는 그래프는 일반적으로 알고 있던 그래프 형태와는 좀 달랐다.
😫 (역시 새롭다 ..)
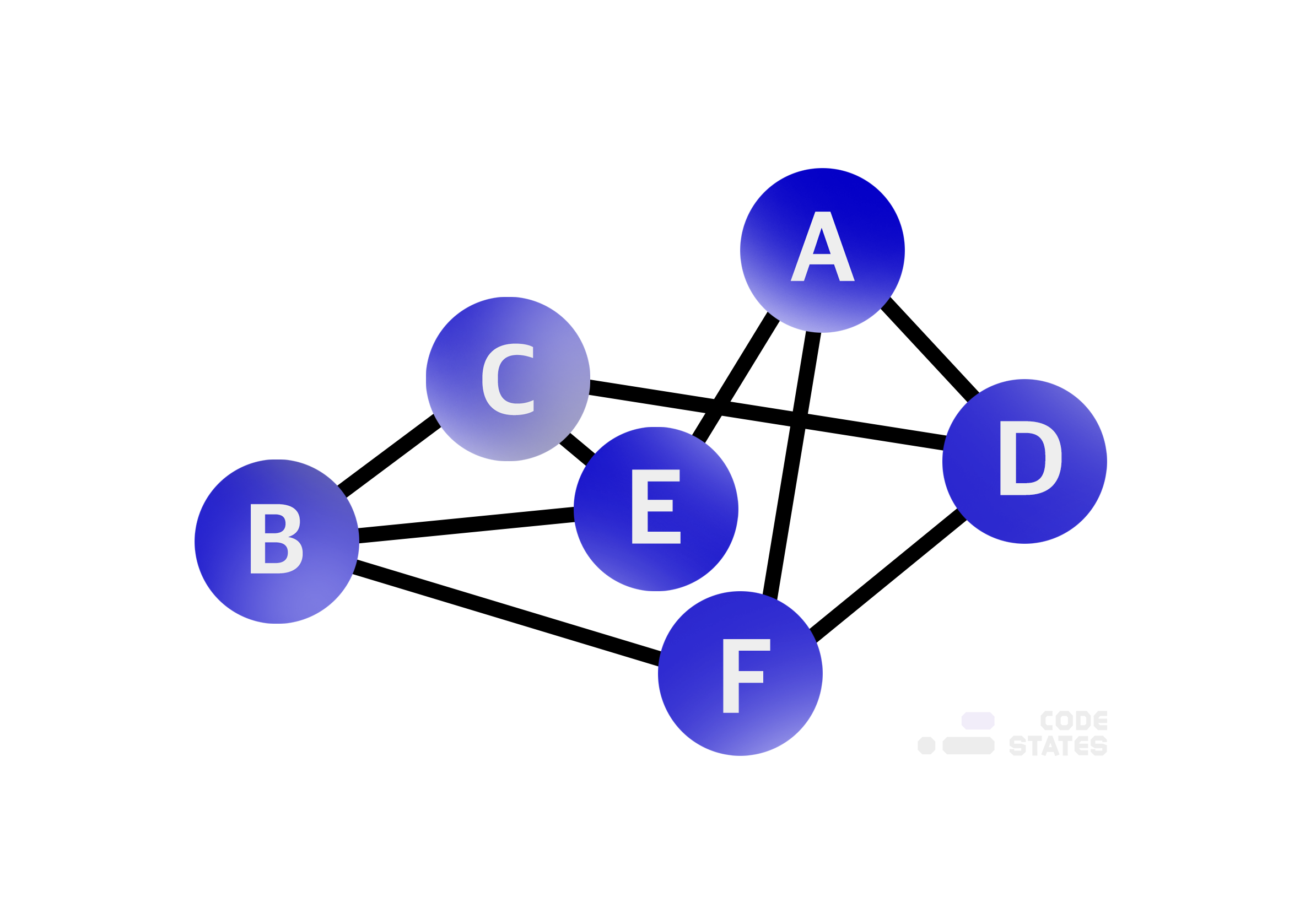
점은 그래프에서 정점(vertax)이라고 표현
선은 간선(edge)이라고 표현한다.
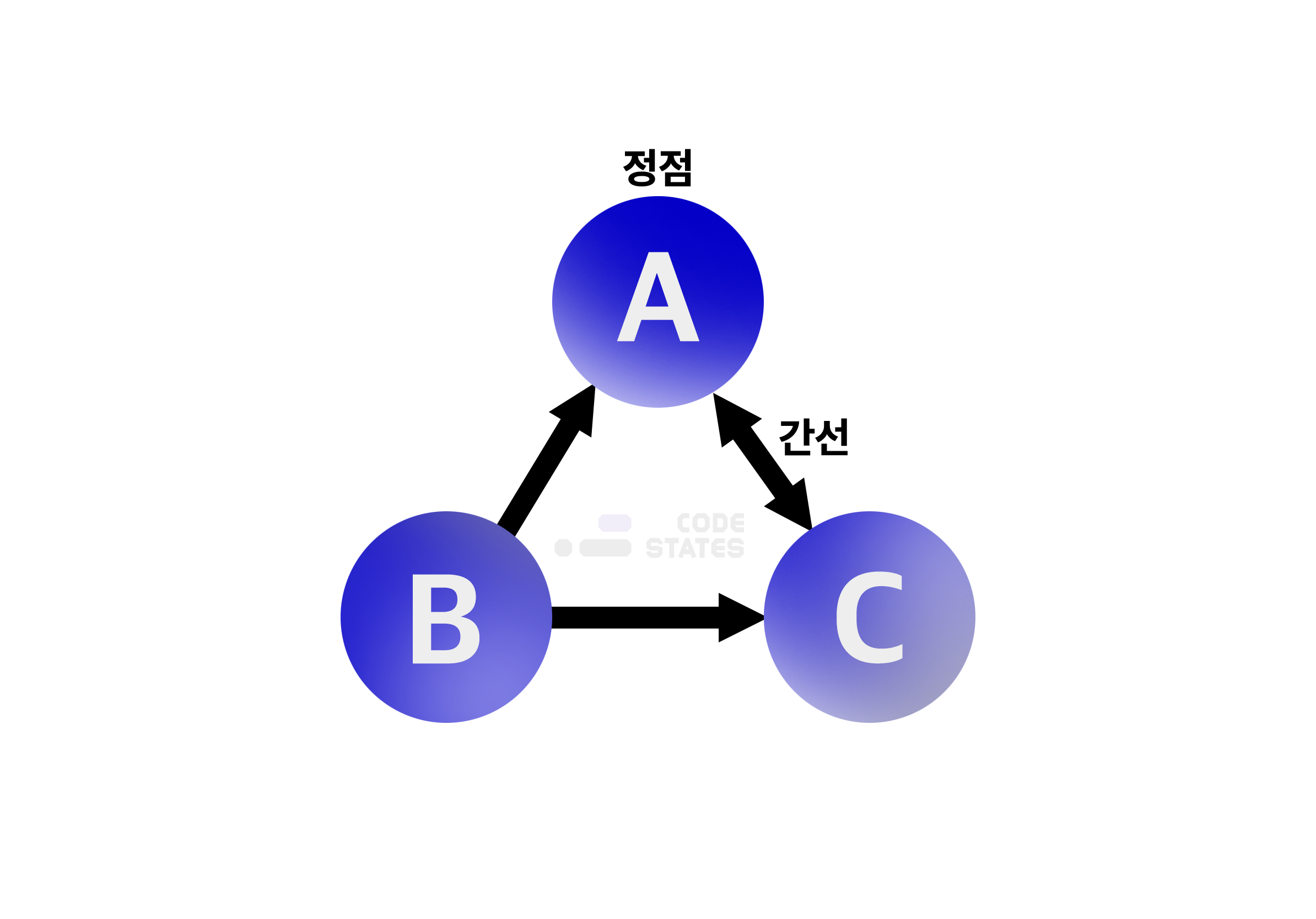
인접행렬
두 정점을 바로 이어주는 간선이 있다면 이 두 정점은 인접하다라고 할 수 있다.
인접행렬은 정점들간의 인접합을 표시해주는 행렬로 2차원 배열의 모습을 하고 있다.
정점이 이어져있으면 1, 아니면 0
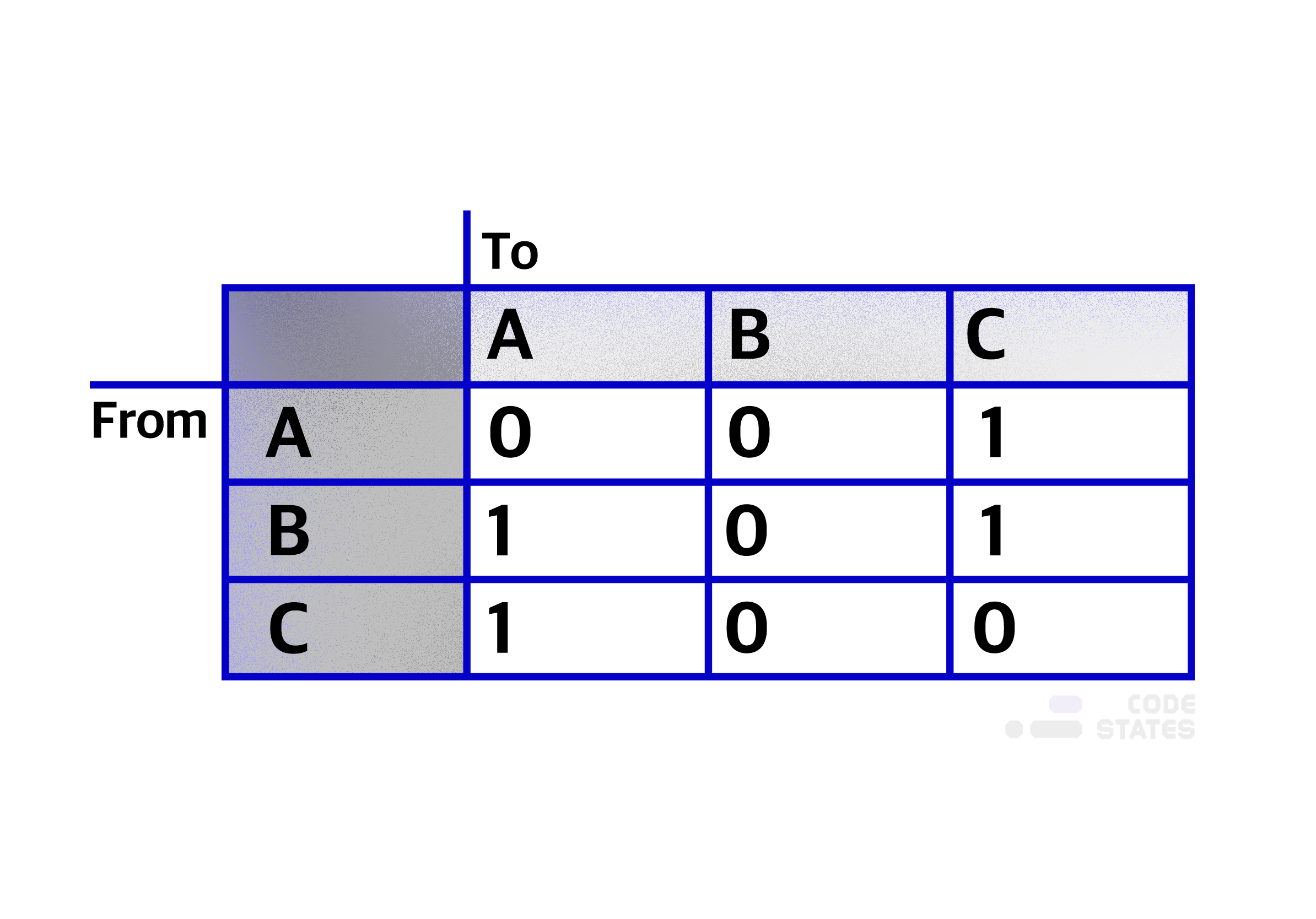
- A의 진출차수는 1개 입니다: A —> C
[0][2] === 1 - B의 진출차수는 2개 입니다: B —> A, B —> C
[1][0] === 1
[1][2] === 1 - C의 진출차수는 1개입니다: C —> A
[2][0] === 1
인접행렬은 언제 쓰면 좋을까?
-
두 정점 사이에 관게의 유무를 확인하는데 용이함
-
A에서 B로 진출하는 간선의 유무를 알기 위해서는 0번째 줄의 1번쨰 열에 저장된 값으로 파악이 가능하다!
-
가장빠른 경로찾기를 할때 (shortest path)
인접리스트
각 정점이 어떤정점과 인접한지 리스트형태로 나타난 표현방식
각 정점마다 하나의 리스트를 가지며, 이 리스트에는 자신과 인접한 다른 정점들이 담겨 있다.
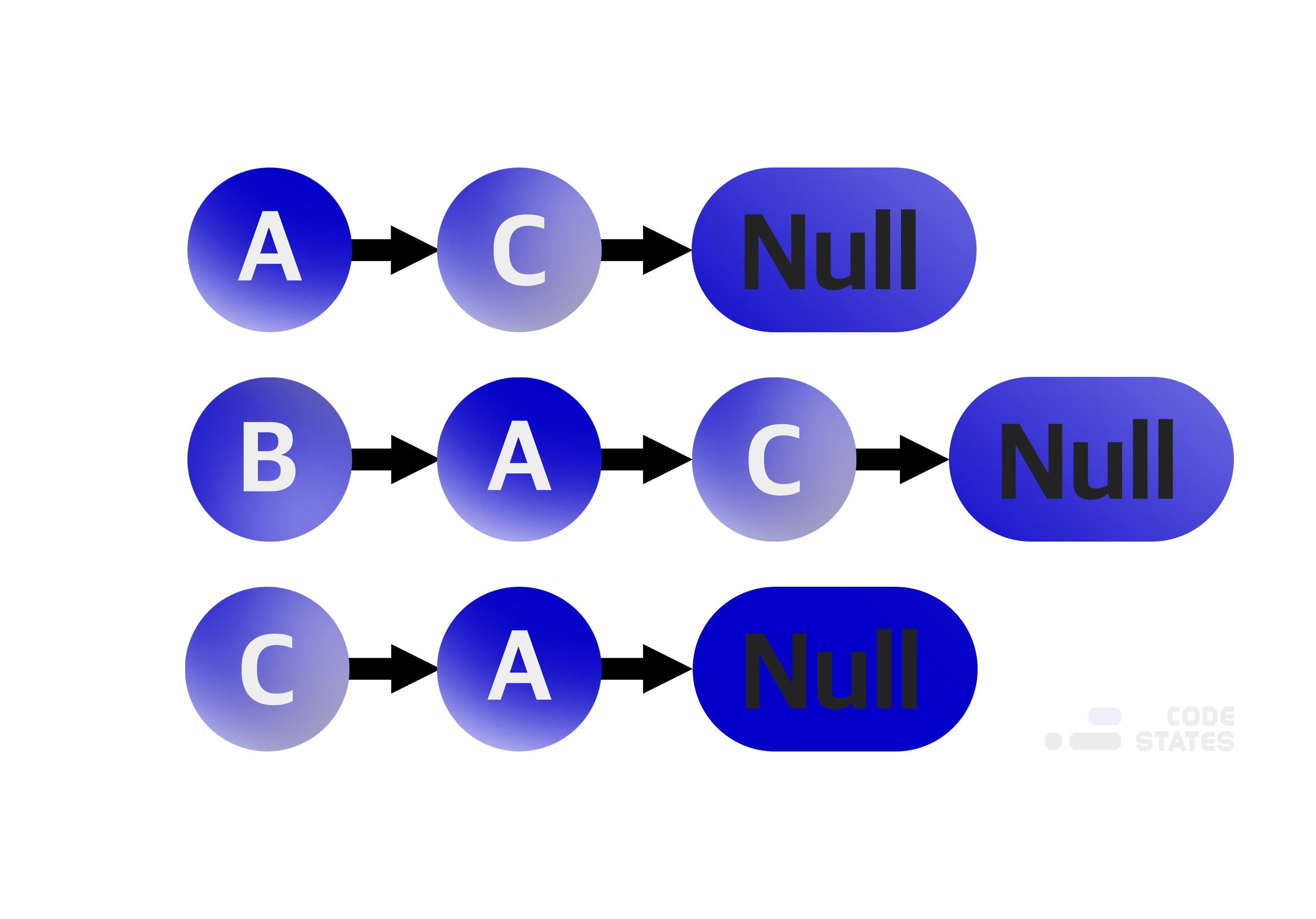
인접리스트는 언제 쓰면 좋을까?
- 인접 행렬은 연결 가능한 모든 경우의 수를 저장
- 서로 인접하지 않다면 0을, 인접하다면 1을 저장하기 때문에 메모리를 많이 차지하게 됩니다.
- 메모리를 효율적으로 사용하고 싶다면 인접 행렬 대신 인접 리스트를 사용합니다.
2. Tree
그래프의 여러 구조 중 일방향 그래프의 한 구조로, 그 모습이 나무와 닮아 있다고 해서 트리 구조라는 이름이 붙여졌다.
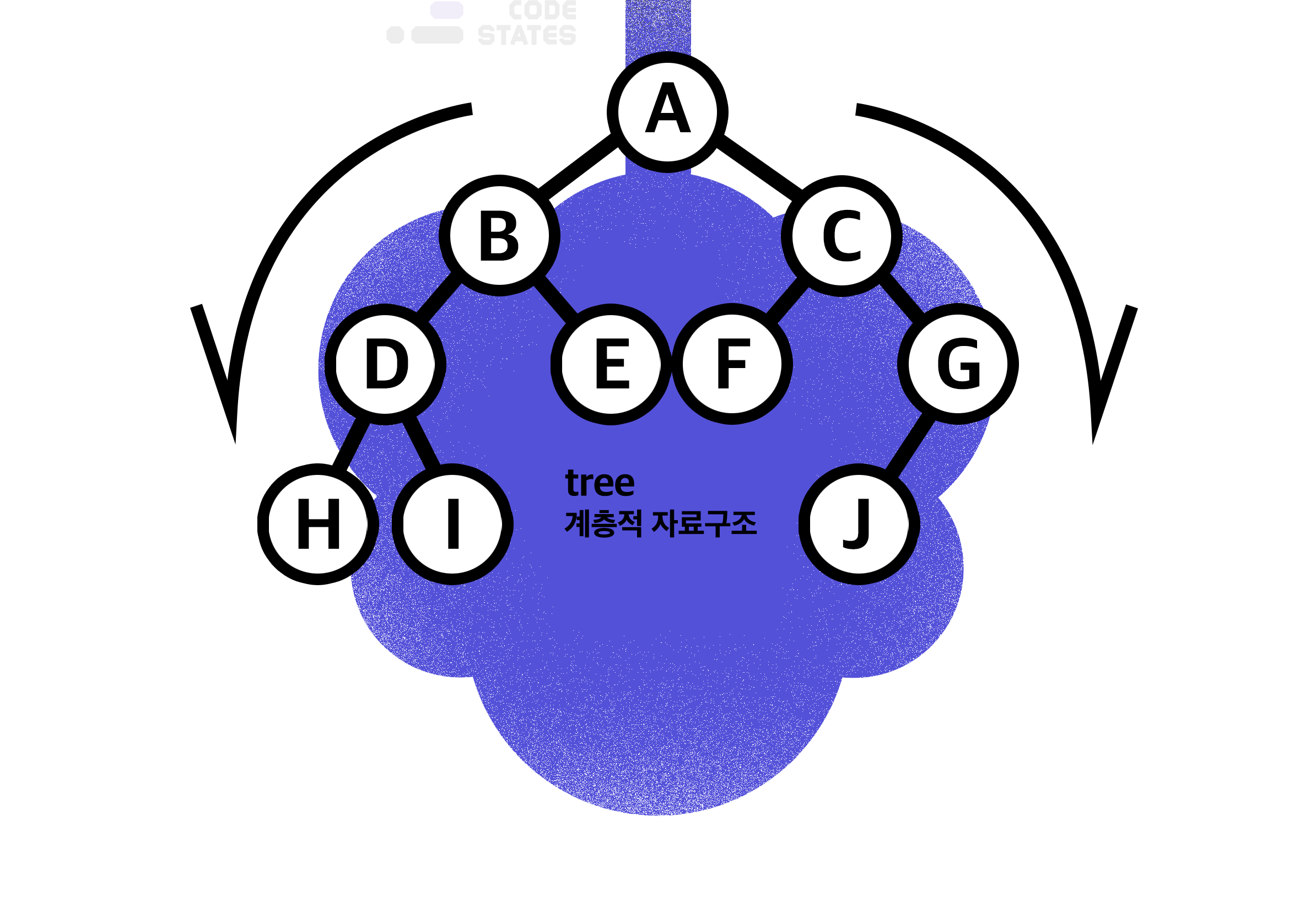
- 트리 구조는 루트(Root)라는 하나의 꼭짓점 데이터를 시작으로 여러 개의 데이터를 간선(edge)으로 연결.
- 이 데이터들을 노드(Node)라고 하며, 상위 노드와 하위 노드가 연결이 되면 부모/자식 관계를 가지게 된다.
- A는 B와 C의 부모 노드(Parent Node)
- B와 C는 A의 자식 노드(Child Node)
- 자식이 없는 노드는 리프 노드(leaf Node)라고 한다.
트리의 실사용 예제
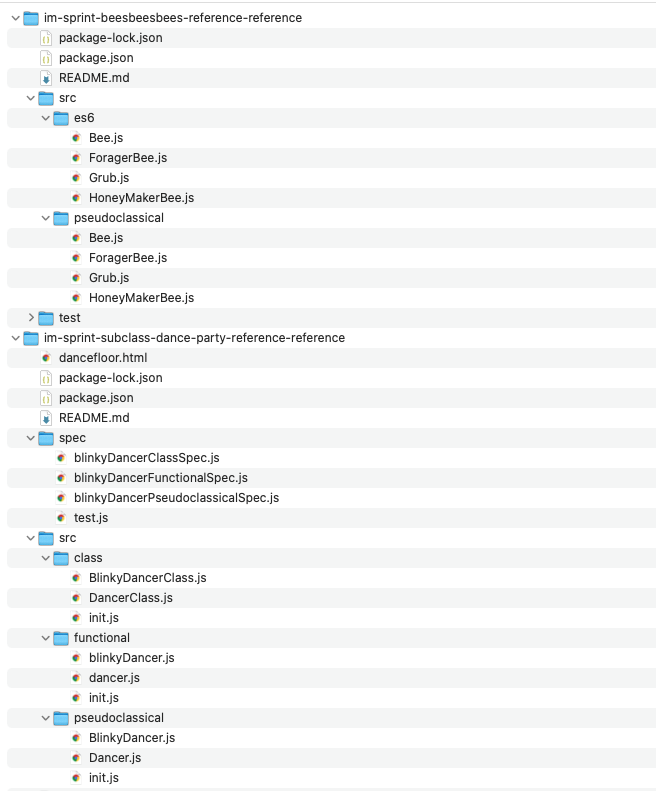
우리가 이미 잘알고 있는 컴퓨터 디렉토리의 구조를 보면 알 수 있다. 가장 상위의 폴더로 부터 아래로 내려가는 구조를 살펴 볼 수 있다. 제일 첫 번째 폴더로 가는 경로는 유일하다!!
파일 시스템과 같은 구현은 모두 트리를 이용해서 만든다.
3. BST (Binary Search Tree)
자식 노드가 최대 2개인 노드들로 구성된 트리를 이진 트리라고 정의
이 2개의 노드는 왼쪽 자식과 오른쪽 자식으로 분류
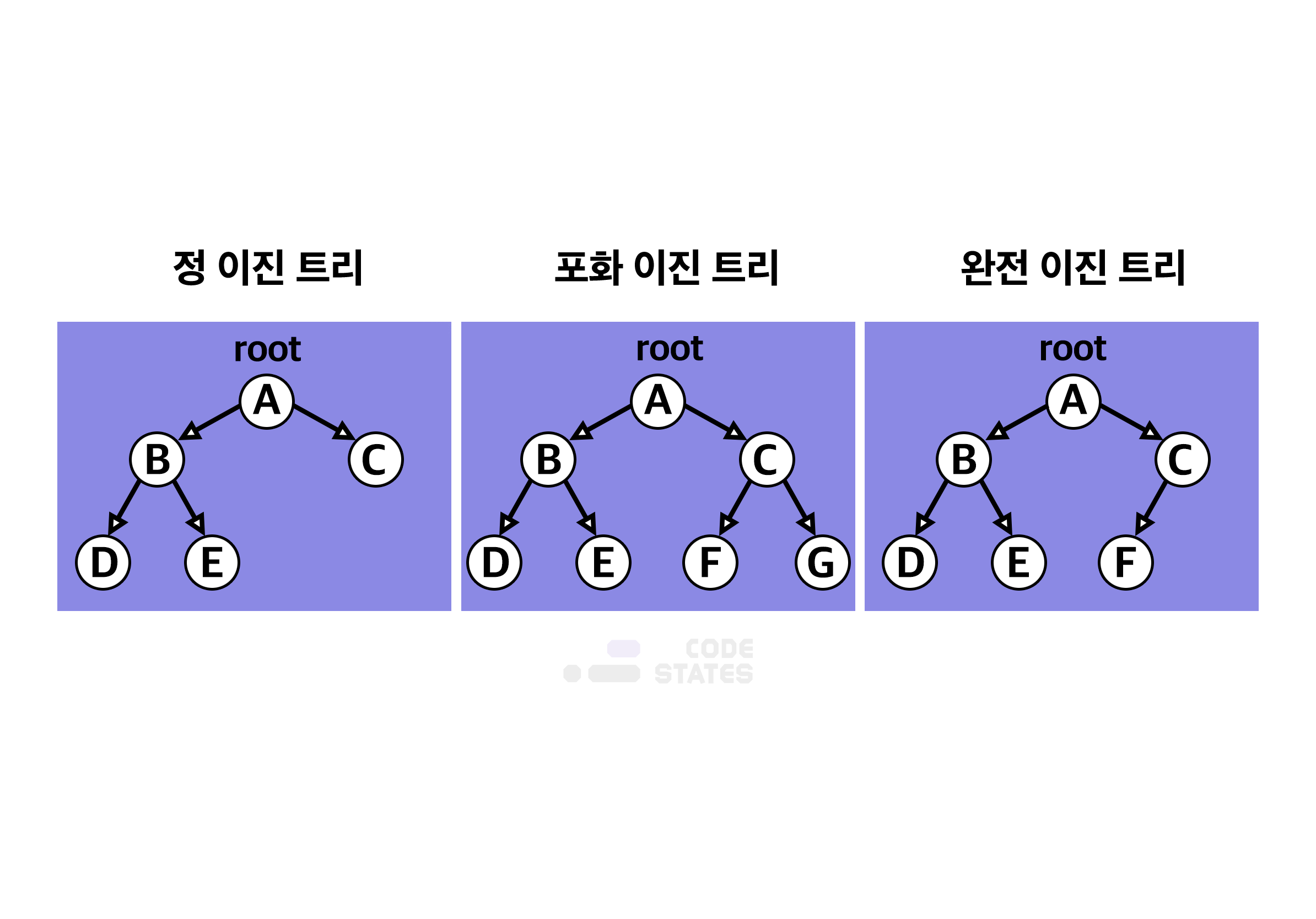
- 정 이진 트리 : 각 노드가 0개 혹은 2개의 자식 노드를 갖는다.
- 완전 이진 트리 : 마지막 레벨을 제외한 모든 노드가 가득 차 있어야 하고, 마지막 레벨의 노드는 전부 차 있지 않아도 되지만 왼쪽이 채워져야 한다.
- 포화 이진 트리 : 정 이진 트리이면서 완전 이진 트리인 경우이다. 모든 리프 노드의 레벨이 동일하고, 모든 레벨이 가득 채워져 있는 트리이다.
모든 왼쪽 자식들은 루트나 부모보다 작은 값이고, 모든 오른쪽 자식들은 루트나 부모보다 큰 값인 특징을 가지고 있는 이진 트리를 이진 탐색 트리라고 정의
마무리
아직은 낯설고 어렵게 느껴지는 부분이라서 계속 접해보고 문제를 풀고 부딪쳐봐야지 데이터 구조 파트는 내것이 될것같다 ㅎㅎ...
다행히 다른 동기들 한테도 물어보니 이파트가 어렵고 힘들다고 한다.
(전부는 아님 ㅋㅋ 잘하는 분들은 역시 잘해)
어찌되었든 낙심하지말고 계속해서 공부해보자!! 아직 데이터구조 1주일밖에 안했으니깐 🔥🔥🔥🔥🔥🔥
