
정규화가 필요한 이유
데이터베이스를 잘못 설계하면 불필요한 데이터 중복으로 발생하는 공간낭비 및 부작용을 초래할 수 있습니다. 이러한 부작용을 이상(Anomaly) 이라고 하는데, 이상 현상의 종류로 삽입이상, 갱신이상, 삭제이상이 있습니다.
삽입 이상 (Insertion Anomaly)
새 데이터를 삽입하기 위해 불필요한 데이터도 함께 삽입해야 하는 문제를 삽입이상 이라고 합니다.
예를들어 Key로 지정된 Attribute는 NULL이 될 수 없습니다. 하지만 NULL인 하는 데이터가 있다면 그 데이터는 테이블에 추가될 수 없습니다. 그 데이터를 추가하려면 굳이 'NULL' 용 속성을 따로 만들어서 삽입해야 합니다.
갱신 이상 (Update Anomaly)
중복된 튜플 중 일부만 변경하여 데이터가 불일치하게 되는 모순의 문제를 갱신이상 이라고 합니다.
예를들어 기본키에 종속되어 있는 Attribute가 변경된다면 모두 변경되어야 합니다. 여기서 모두 변경되지 않는 경우 데이터의 모순성이 발생하게 됩니다.
삭제 이상 (Deletion Anomaly)
튜플을 삭제할때 꼭 필요한 데이터 까지 함께 삭제되는 데이터 손실의 문제를 삭제이상 이라고 합니다.
예를들어, 튜플에서 특정 Attribute를 삭제하려고 할 때 그 Attribute가 기본키라면 해당 테이블에 반영하기 위해 모든 행을 삭제해야 합니다.
왜 이런 문제가 발생할까요?
위와 같은 이상현상들이 발생하는 이유는 정규화가 되어 있지 않은 테이블 설계 때문입니다. 코딩할 때에도 관심사를 분리하면 코드의 재사용성과 유지보수의 편의성이 높아지는 것처럼 데이터베이스 설계에서도 비슷한 원칙이 적용됩니다. 데이터베이스 설계의 경우 관심사를 분리하지 않아 생기는 문제는 코드에서의 문제보다 훨씬 치명적입니다.
이론적으로는 정규화를 수행하려면 속성들간의 관련성을 파악해야 하는데, 이 속성들간의 관련성을 함수적 종속성(Functional Dependency) 이라고 합니다. 일반적으로 하나의 릴렝션에는 하나의 함수적 종속성만이 존재하도록 정규화를 하게 됩니다.
함수적 종속성 (Functional Dependency)
함수적 종속성은 아래와 같이 표현할 수 있습니다.
X→Y
- X는 결정자, Y는 종속자라고 합니다.
- X가 Y를 함수적으로 결정합니다.
- Y가 X에 함수적으로 종속되어 있습니다.
Example 1

위와 같은 학생 릴레이션을 예제로 들어 함수적 종속성을 알아보겠습니다.
학번에 의해 학생이름과 학부는 고유하게 구분되므로 학생이름, 학부 속성은 학번에 함수적으로 종속되어 있습니다. 여기서 학번은 결정자, 학생 이름과 학부는 종속자가 되며, 함수적 종속성은 아래와 같은 기호로 표현할 수 있습니다.
학번 → {학생이름, 학부}
주의할 점은 현시점의 속성 값만으로 판단하면 안됩니다. 속성 값은 계속 변할 수 있는 것이기 때문에 속성 자체가 가지는 특성과 의미를 기반으로 판단해야 합니다.
Example 2
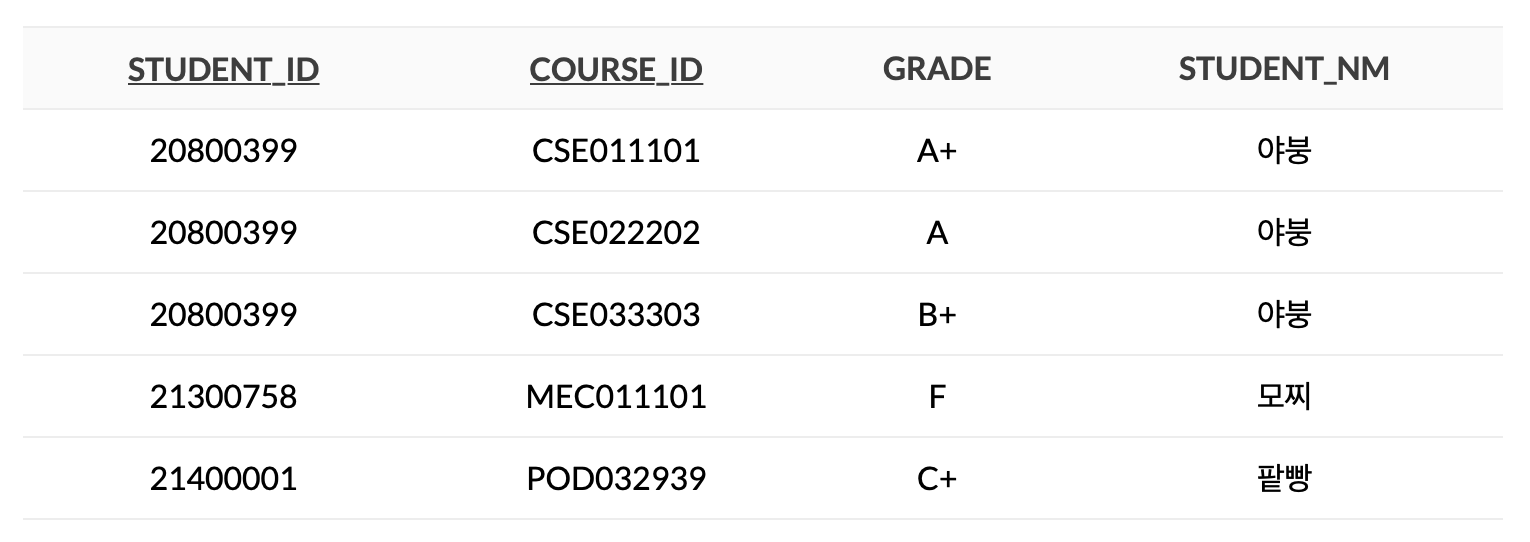
위 릴레이션에서 함수적 종속성은 아래와 같이 정의할 수 있습니다.
학번 → 이름
{학번, 과목코드}→ 성적
{학번, 과목코드}→ 이름
- 이름을 결정짓는 요소는 학번입니다.
- 성적을 결정짓는 요소는 학번과 과목코드입니다.
- 이름은 학번과 과목코드에 의해서도 고유하게 구분될 수 있습니다.
이름의 경우 해당하는 함수적 종속성이 두개입니다. 여기서 부분 함수적 종속과 완전 함수적 종속 을 구분할 수 있습니다.
부분 함수적 종속 (Partial Functional Dependency)
속성집합 Y가 속성집합 X의 전체가 아닌 일부분에도 함수적으로 종속됨을 의미합니다.
이름이 속성집합 Y이고, {학번, 과목코드}가 속성집합 X인 상태에서, 이름은 {학번, 과목코드} 에도 함수적으로 종속되며 X의 일부인 학번에도 함수적으로 종속됩니다.
완전 함수적 종속 (Full Functional Dependency)
이름이 속성집합 Y이고, {학번, 과목코드}가 속성집합 X인 상태에서, 성적은 {학번, 과목코드} 의 어떤 부분집합에도 함수적으로 종속되어 있지 않습니다. 학번만으로 성적을 결정지을 수 없고, 과목코드만으로도 성적을 결정지을 수 없기 때문입니다.
일반적으로 함수적 종속성을 말하면 완전함수종속을 의미합니다.
정규화 (Normalization)
정규화는 관계형 데이터베이스의 설계에서 중복을 최소하하게 데이터를 구조화하는 프로세스를 정규화라고 합니다.
조금 더 이론적으로 접근해 보면, 함수적 종속성을 이용해서 연관성 있는 속성들을 분류하고, 각 릴레이션들에서 이상현상이 생기지 않도록 하는 과정을 말합니다.
정규화가 진행된 정도를 정규형(Normal Form)으로 표현하는데, 정규형에는 1NF, 2NF, 3NF, BCNF, 4NF, 5NF, 6NF 까지 있습니다. 비공식적 표현으로는 3NF가 되었으면 정규화 되었다고 말합니다. 3NF 테이블의 대부분이 삽입, 변경, 삭제 이상이 없으며, 3NF 테이블의 대부분이 BCNF, 4NF, 5NF 입니다.
각 정규형이 되기 위해서는 만족시켜야 할 제약조건들이 있습니다. 높은 차수의 정규형으로 갈 수록 조건이 까다롭습니다.
제 1정규형 (1NF - First Normal Form)
제 1정규형은 릴레이션에 속한 모든 속성의 도메인이 원자 값으로만 구성되어 있으면 제 1정규형에 속합니다.

위와 같은 형태의 릴레이션은 제 1정규형을 만족하지 않습니다. 최소한 아래와 같은 형태가 되어야 제 1정규형을 만족합니다.
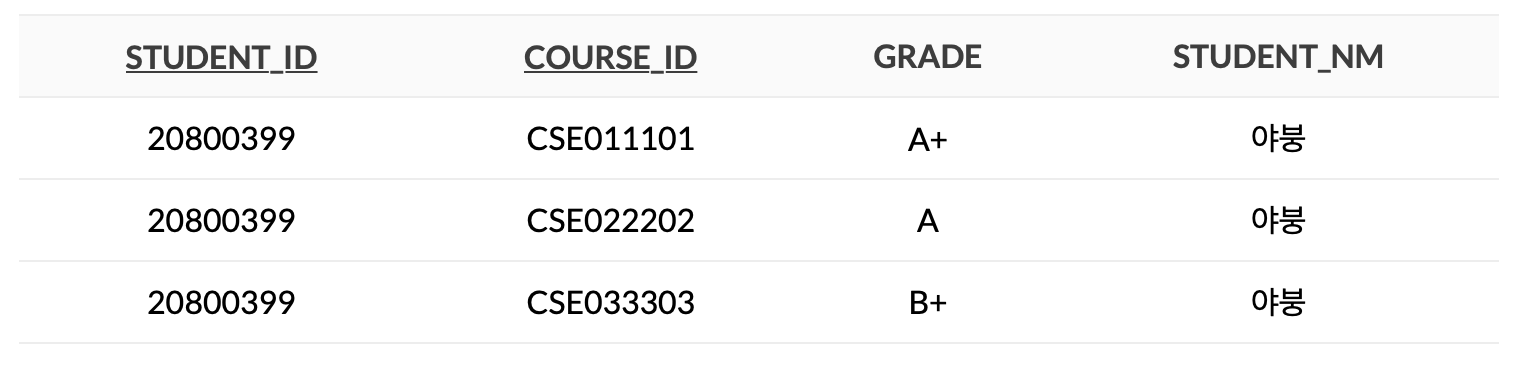
제 2정규형 (2NF - Second Normal Form)
제 1정규형만 만족시키는 릴레이션에서 부분 함수 종속성을 가지게 되는 경우 삽입이상, 갱신이상, 삭제이상 세가지 이상현상이 모두 나타나게 됩니다.
제 1정규형에 속하면서, 기본키가 아닌 모든 속성이 기본키에 완전 함수 종속되면 제 2정규형 입니다.
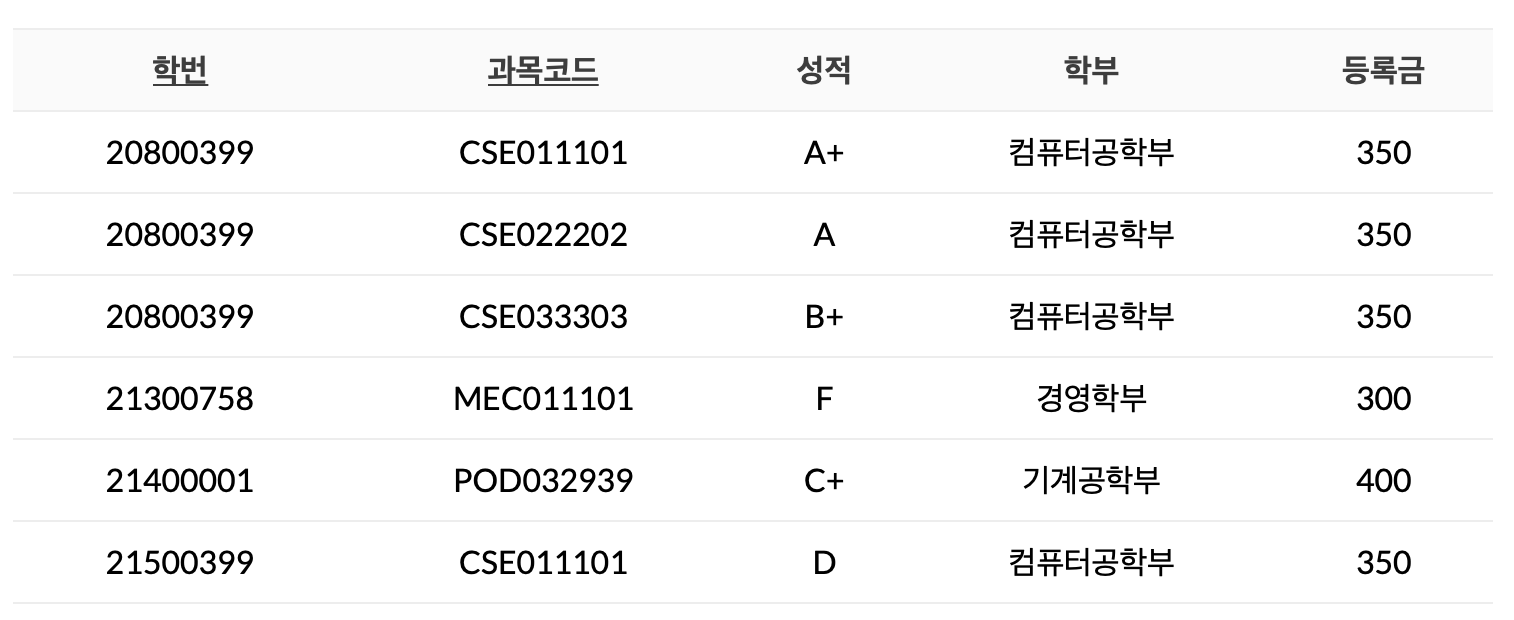
위 릴레이션의 함수적 종속성을 살펴보면 아래와 같습니다.
{학번, 과목코드} → 성적
{학번, 과목코드} → 학부
{학번, 과목코드} → 등록금
학번 → 학부
학번 → 등록금
학부 → 등록금
현재 학번→학부, 학번→등록금 두개의 부분 함수 종속성을 가지고 있습니다. 이를 제거해 주는 것을 제 2정규화라고 합니다.
이 경우 학번, 학부, 등록금 속성을 가지는 학생 릴레이션과 학번, 과목코드, 성적 속성을 가지는 성적 릴레이션 둘로 나누어 주면 부분 함수 종속성을 제거할 수 있습니다.
학번 → 학부 함수종속성으로 볼때, 학번만으로 학부에 대한 결정을 지을 수 있습니다. 그러나 현재 기본키가 학번, 과목코드로 이루어져 있기 때문에 학번만으로 학부에 대한 결정을 지을 수 있다는게 의미가 없어집니다. 그래서 이를 가능하도록 해주는 과정이 부분 함수 종속성 을 제거하는 2정규화 과정입니다.
여기서 학부→등록금 이라는 함수적 종속은 부분 함수 종속성이 아닙니다. X→Y 라는 함수적 종속성에서 부분 함수 종속성, 완전 함수 종속성을 따질 때, 결정자 X가 반드시 기본키나 후보키에 속할 필요는 없으므로, 현재 학부→등록금의 함수 종속은 하나의 완전 함수 종속이라고 볼 수 있습니다.
학번→학부, 학번→등록금 두개의 부분 함수 종속성을 제거하여 분리한 두개의 릴레이션은 아래와 같습니다.
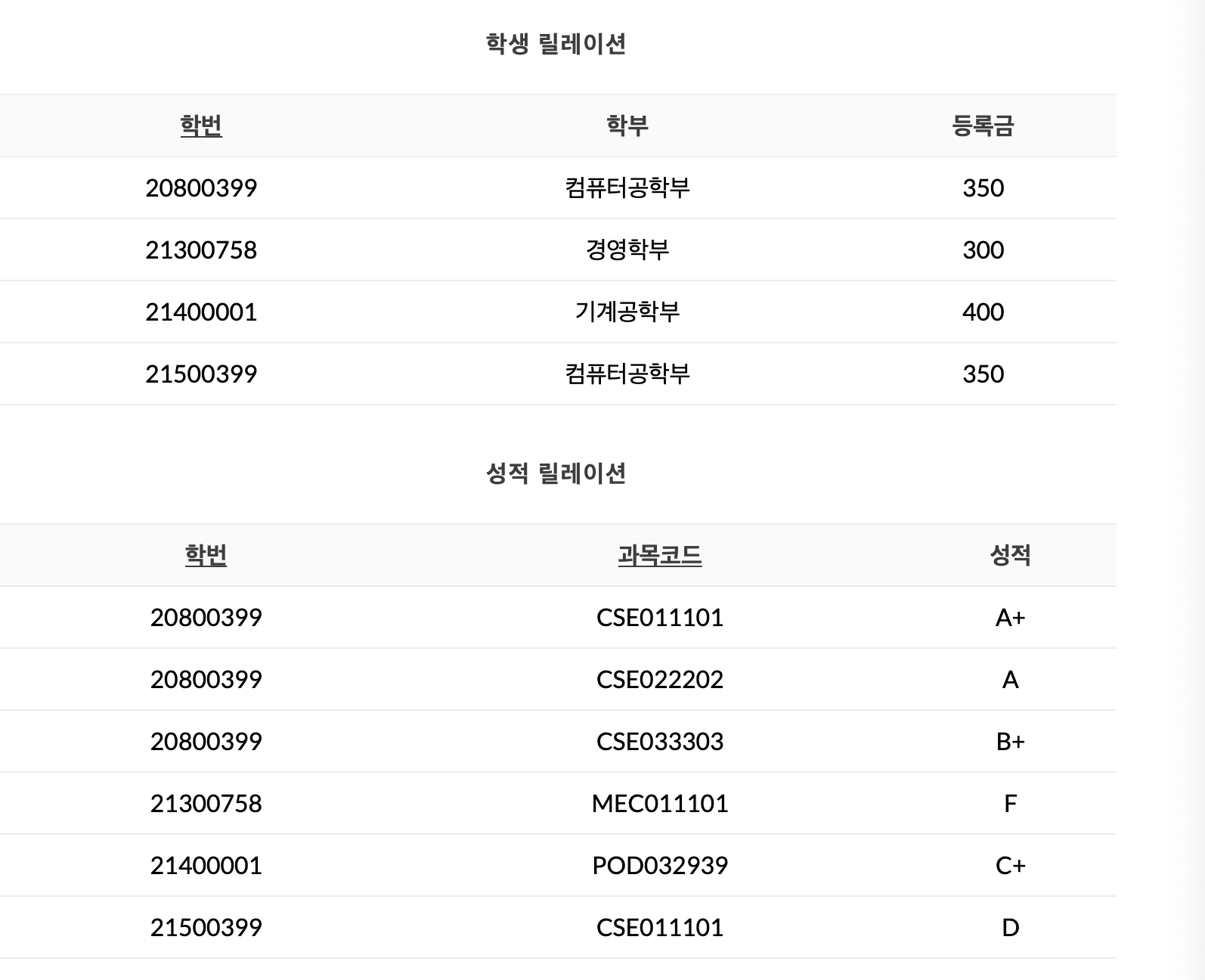
릴레이션이 둘로 분해되면서 학부와 등록금에 대한 중복항목이 제거되었습니다. 정규화 과정에서 주의할 점은 정규화를 통해 분해된 릴레이션들이 조인을 통해 원래의 구조로 복원될 수 있어야 한다는 것을 유의해야 합니다.
두 릴레이션 모두 제 1정규형에 속하고, 기본키가 아닌 모든 속성이 기본키에 완전 함수 종속되므로 제 2정규형을 만족합니다.
제 2정규형을 만족하면 이상현상이 없어질까요?
삽입 이상
새로운 학부가 생기는 경우 등록된 학생(학번)이 없다면 학번속성이 NULL이 되므로 삽입할 수 없습니다.
갱신 이상
컴퓨터공학부 등록금이 400으로 오르는 경우 20800399, 21500399 둘 모두 바꾸어 주지 않으면 데이터 불일치 문제가 발생합니다.
삭제 이상
21400001 학번을 가진 학생이 자퇴하는 경우, 기계공학부에 대한 정보가 함께 사라집니다.
제 2정규형에서도 이상현상이 발생하는 이유는 이행적 함수 종속 이 존재하기 때문입니다. 이행정 함수 종속을 없애주는 과정이 제 3정규화 입니다.
제 3정규형 (3NF-Third Normal Form)
제 3정규형은 제 2정규형에 속하면서, 기본키가 아닌 모든 속성이 기본키에 이행적 함수 종속이 되지 않으면 제 3정규형 입니다.
이행적 함수 종속?
이행적 함수 종속은 삼단 논법같은 관계를 가진 함수 종속입니다. X, Y, Z에 대해 X→Y 이고, Y→Z 이면 X→Z가 성립합니다. 이를 Z가 X에 이행적으로 함수 종속되었다고 합니다.
현재 학생릴레이션에서 함수적 종속성은 아래와 같습니다.
학번→학부
학부→등록금
학번→등록금
X→Y, Y→Z 함수적 종속관계로 인해 X→Z의 이행적 함수 종속 관계가 나타나면, [X, Y], [Y,Z] 두 릴레이션으로 분해하면 됩니다.
이 둘을 분리하여 이행적 종속 관계를 제거 한 학생 릴레이션과 학부 릴레이션은 아래와 같습니다.

