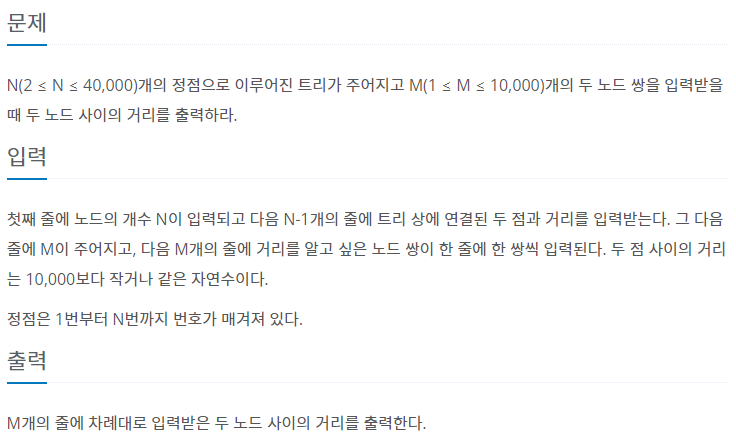
문제
- 시간 제한: 2초
- 메모리 제한: 128MB
Problem Analysis
두 정점을 잇는 경로를 찾아야한다. 이때, Tree는 계층적인 구조이기 때문에, 두 정점을 잇는 최상단 node인 Lowest common ancestor(LCA)를 찾으면 경로를 쉽게 이을 수 있을 것이다.
Algorithm
- 1번 node를 root로 하여, DFS를 진행하여 다음의 데이터를 만든다
- Range Minimum Query(RMQ)용 segment Tree
- 각 node의 root로부터 떨어진 거리
- RMQ를 통해 LCA를 찾는다. 이후 |a의 거리| + |b의 거리| - 2*|lca의 거리|를 출력한다.
Data Structure
- segment Tree[]: euler tour 번호를 index로 하여, 구간에서의 최소 level을 저장.
- dfsLog_node[]: euler tour 각 차례에 접근한 node 번호
- dfsLog_level[]: euler tour 각 차례에 접근한 node의 level
- firstOccurOfNode[]: 각 node가 처음 나타난 euler tour 번호
- distFromRoot[]: 각 node가 root로부터 떨어진 거리
결과

Other
시간 복잡도는 segTree 생성에 O(N), 각 query 마다 O(logN)이다.
