Weisfeiler-Lehman Graph Kernels

Weisfeiler-Lehman Graph Kernels
https://www.jmlr.org/papers/volume12/shervashidze11a/shervashidze11a.pdf
에 대한 리뷰입니다.

Weisfeiler-Lehman test를 기반으로 빠르게 그래프의 feature (topological, label information) extraction 하는 것이 목적이고 kernel method를 적용해 large scale & high-dimensional node labels를 갖는 graph들의 classification , similarity 계산에 있어서 효과적인 방법을 제시한다.

Notation

$G =(V, E, \ell)$
$V$ : the set of vertices
$E$ : the set of undirected edges
$\ell :V \rightarrow \Sigma$, WL Algorithm에 의해 새로운 label을 graph node로 mapping하는 함수

Weisfeiler-Lehman test

기존의 WL-test의 경우 relabeling된 node set의 partition이 그 이전과 동일하면 그만두지만, 해당 논문에서는 그냥 n번 반복한다.

Weisfeiler-Lehman graph sequence

WL test에서 새로운 라벨을 할당하는 함수를 $r(\cdot)$라고 했을 때,
$r((V,E,l_i)) = (V,E,l_{i+1})$

높이가 $i$인 Weisfeiler-Lehman graph $G = (V,E,l_{i})$ 일 때,
$\{G_0,...,G_{h}\} = \{(V,E,l_0),(V,E,l_1),...,(V,E,l_h)\}$ 를
높이 h까지의 "Weisfeiler-Lehman graph sequence"라고 한다.

$G_0$는 original graph이다.

Weisfeiler-Lehman kernel

$k_{WL}^{(h)}(G,G') = k(G_0,G_{0}') + k(G_1,G_{1}') + ... + k(G_h,G_{h}')$

에서 $k_{WL}^{(h)}$를 높이가 h인 "Weisfeiler-Lehman kernel" 이라고 하고
$k$를 "base kernel"이라고 한다.

참고로 , 더 일반적인 표현은 다음과 같다.
$k_{WL}^{(h)}(G,G') = \alpha _0k(G_0,G_{0}') + \alpha_1k(G_1,G_{1}') + ... + \alpha_hk(G_h,G_{h}')$
$\alpha_*$ : nonnegative real value

두 경우 모두 당연하게도 base kernel과 WL kernel은 positive semidefinite하다.

The Weisfeiler-Lehman Subtree Kernel

여기서, $k_{WLsubtree}^{(h)}(G,G')$를
Weisfeiler-Lehman subtree kernel on two graphs G and G' with h iterations 라고 정의한다.

The process of WL Subtree Kernel computation

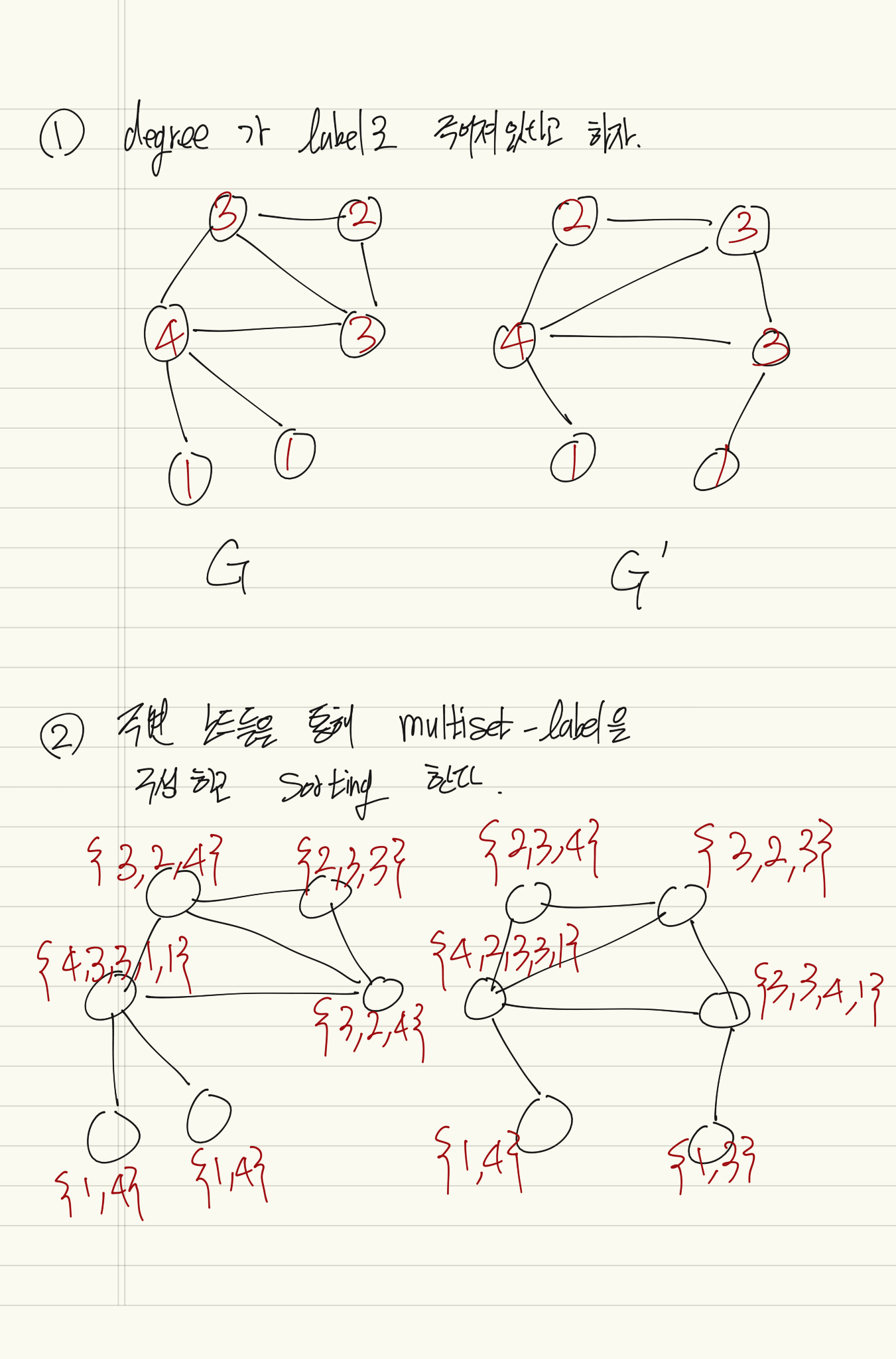
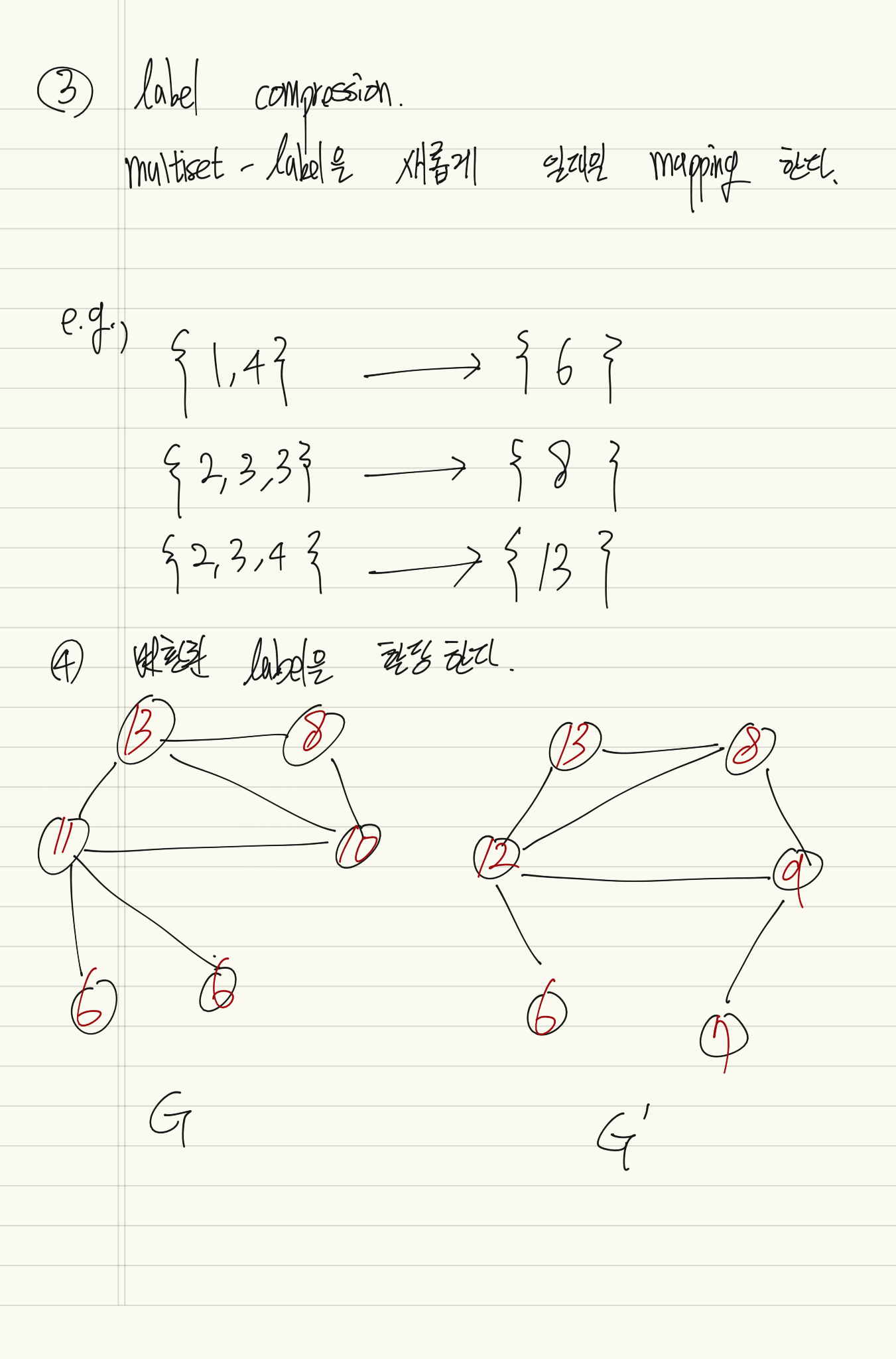
height 수 만큼 iteration 한다.

Subtree pattern 이란

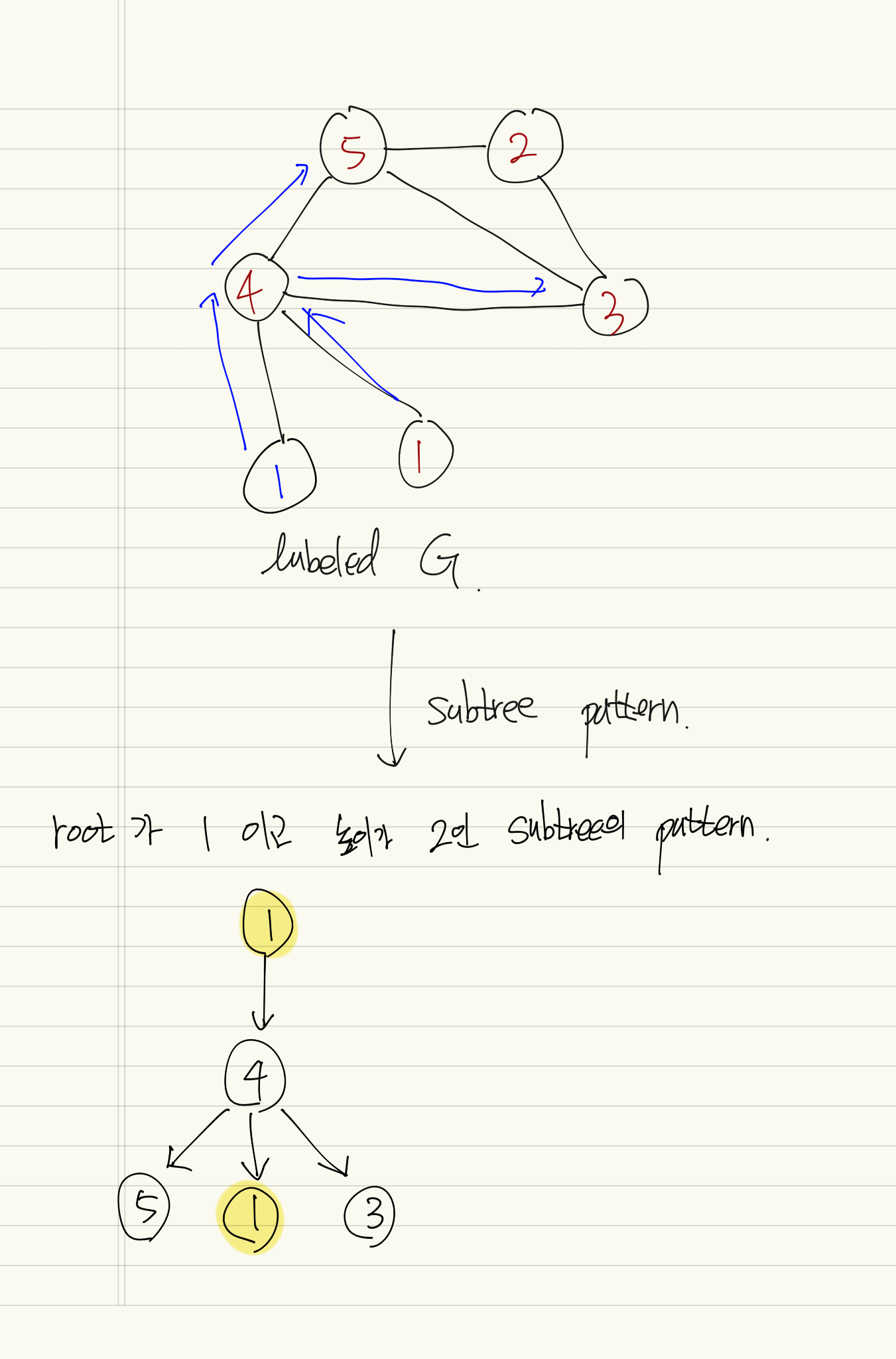
WL Subtree Kernel이라고 부르는 이유

틀릴 수 있음

결론부터 말하자면, the process of WL Subtree kernel computation의 효과가 일치하는 Subtree pattern의 개수를 세는 것과 같기 때문이다.
height = 1인 경우의 간단한 예제를 통한 확인은 다음과 같다.

우선, WL Subtree kernel computation을 해보자.

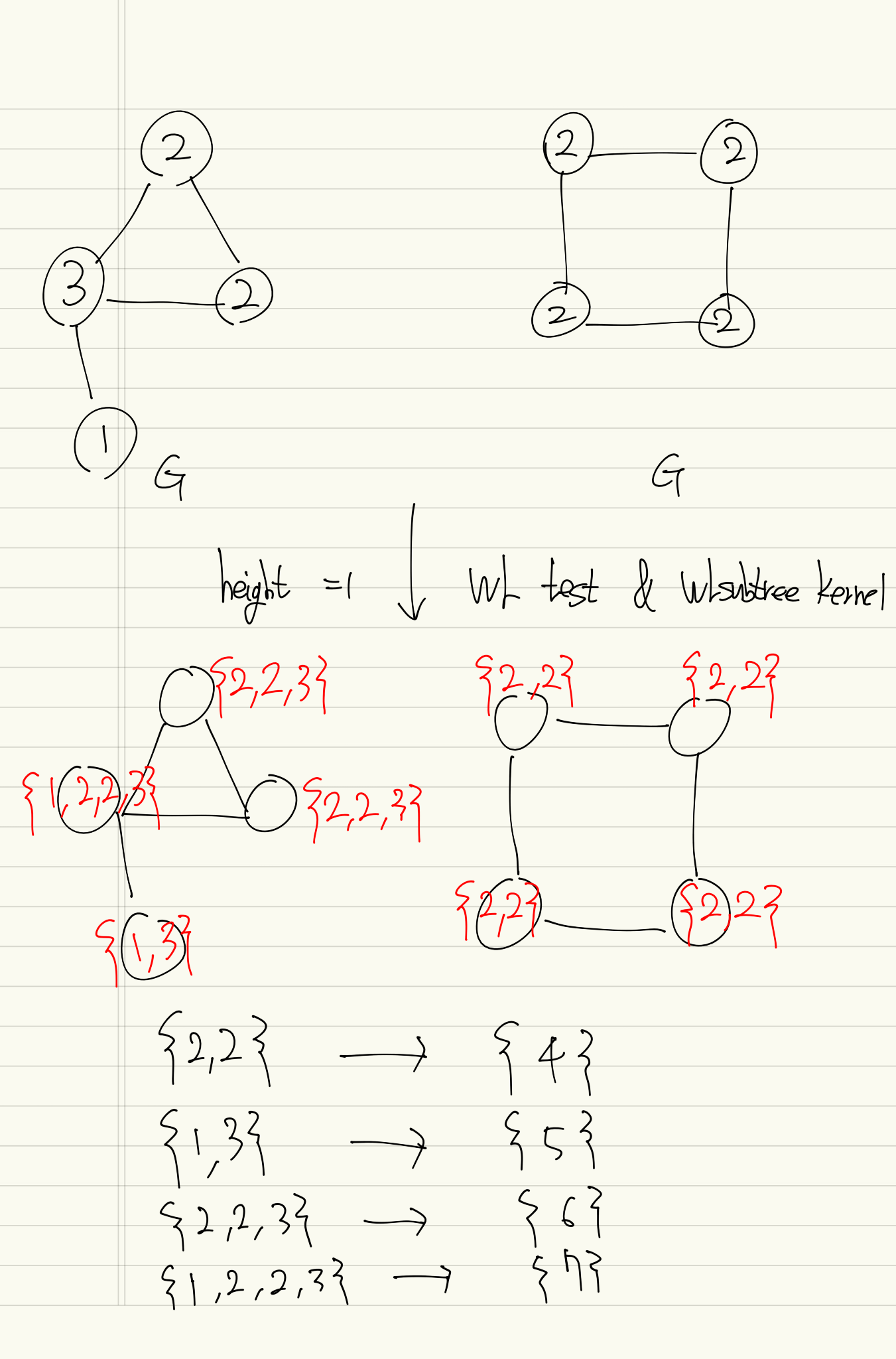
다음으로, height = 1까지 $G,G'$의 일치하는 Subtree의 개수를 세보자.

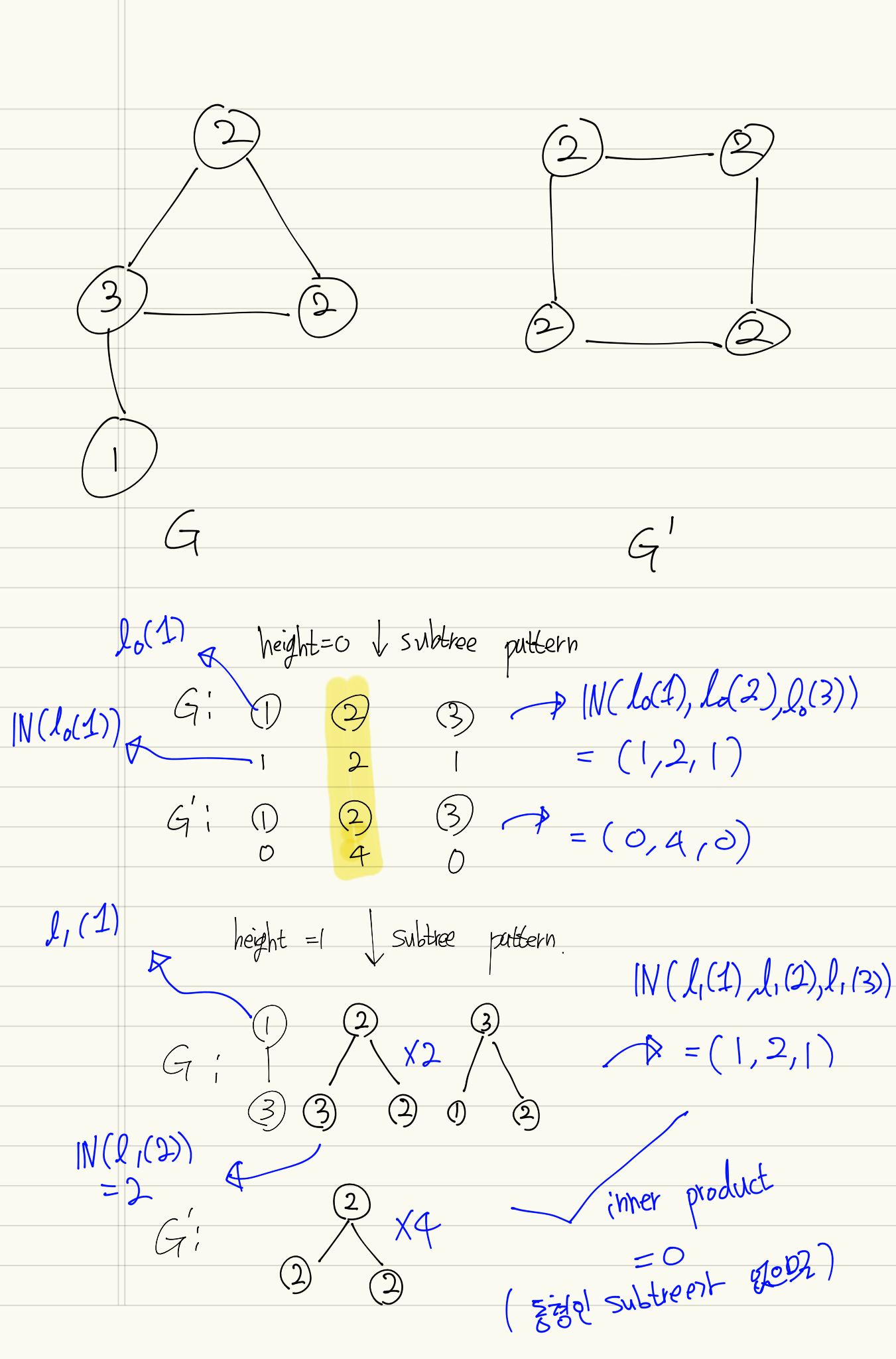
두 그래프의 일치하는 Subgraph의 개수 벡터의 내적 = 8 WL Subtree kernel computation의 결과와 동일하다.

• compressed label $l_i(\nu)$ = root 가 $\nu$이고 height = $i$인 subtree pattern들과 대응된다.

The representation of WL-Subtree kernel with Dirac kernel

Base kernel을 Dirac kernel로 정의하면 그것에 대응하는 WL Kernel은 WL-Subtree kernel이 된다.

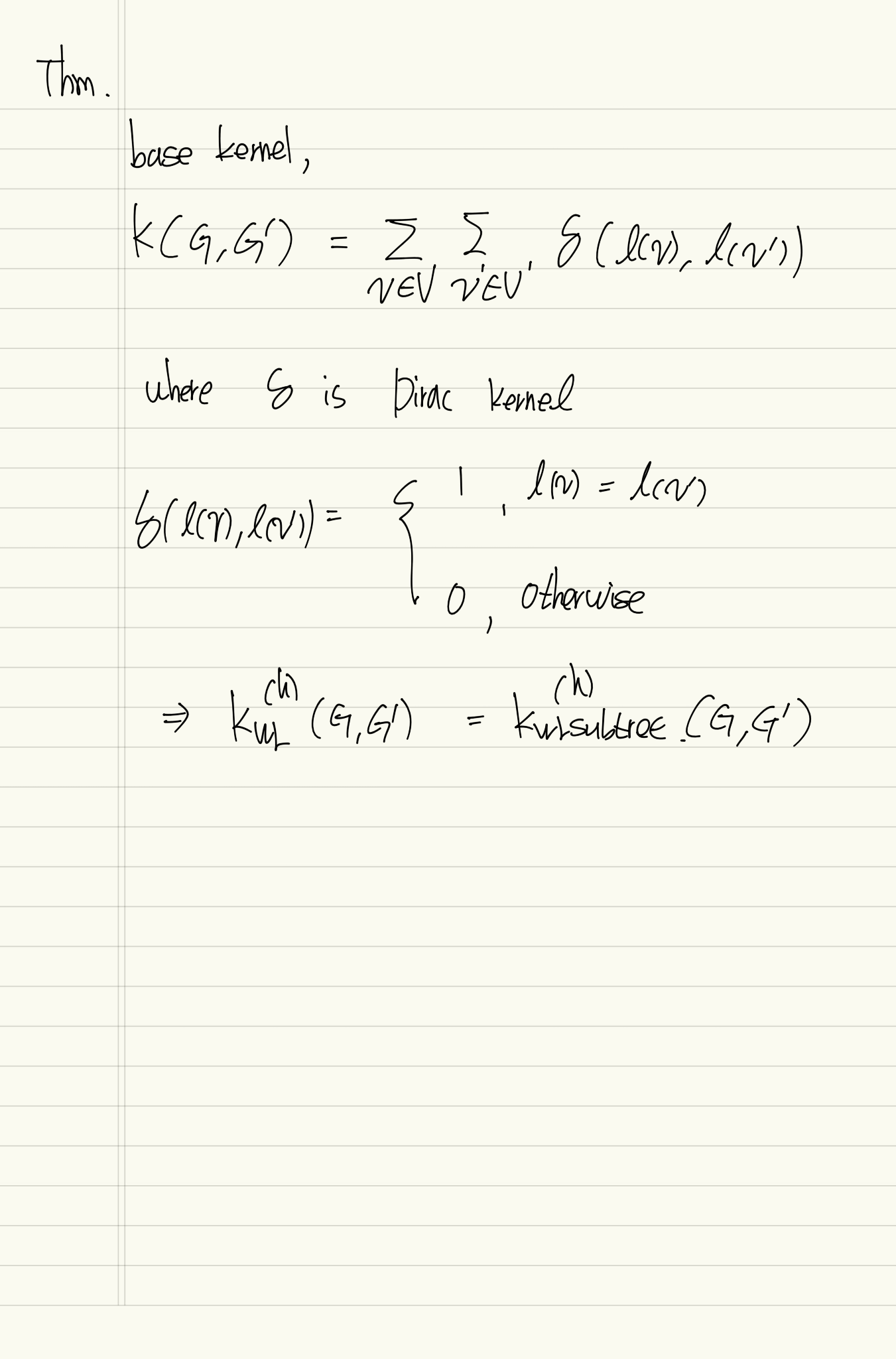
증명생략 .

The Weisfeiler-Lehman Edge Kernel

두 그래프의 유사성을 계산할 때 edge의 endpoint node label들이 동일한지에 대해 고려한다.
즉, edge에 연결되어있는 node pair (a,b)의 개수를 센다.

base kernel $k_E(G,G') = \lang \phi_{E}(G),\phi_{E}(G') \rang$ 라고 했을 때, vector $\phi(G)$는 각각의 성분에 해당하는 제각각의 쌍(a,b)가 등장한 횟수가 된다.

따라서 WL-Edge kernel은 다음과 같다.
$k_{WLedge}^{(h)} = k_{E}(G_{0},G_{0}') + k_{E}(G_{1},G_{1}')+... + k_{E}(G_{h},G_{h}')$

The representation of WL-Edge kernel with Dirac kernel

Edge에 가중치가 동일한 Graph의 경우는 base kernel 은 다음과 같다.
$k_E=\Sigma_{e\in E}\Sigma_{e'\in E'}\delta(a,a')\delta(b,b')$

가중치가 존재하는 경우는 다음과 같다.
$k_E=\Sigma_{e\in E}\Sigma_{e'\in E'}\delta(a,a')\delta(b,b')k_w(w(e),w(e'))$
$where$ $k_w$ is a kernel comparing edge weights.

The Weisfeiler-Lehman Shortest Path Kernel

$k_{SP}(G,G') = \lang \phi_{SP}(G),\phi_{SP}(G') \rang$
vector $\phi_{SP}(G)$는 triplet (a,b,p)이 등장하는 개수를 성분으로 갖는다.
이때, (a,b)는 Edge kernel과 마찬가지로 edge의 endpoint label pair 이고 p는 node a,b 사이의 shortest path length 이다.

따라서 WL-Shortest Path kernel은 다음과 같다.
$k_{WLshortest path}^{(h)} = k_{SP}(G_{0},G_{0}') + k_{SP}(G_{1},G_{1}')+... + k_{SP}(G_{h},G_{h}')$