[자료구조] Python - 이진 탐색 트리(Binary Search Tree, BST) 프로그램 구현

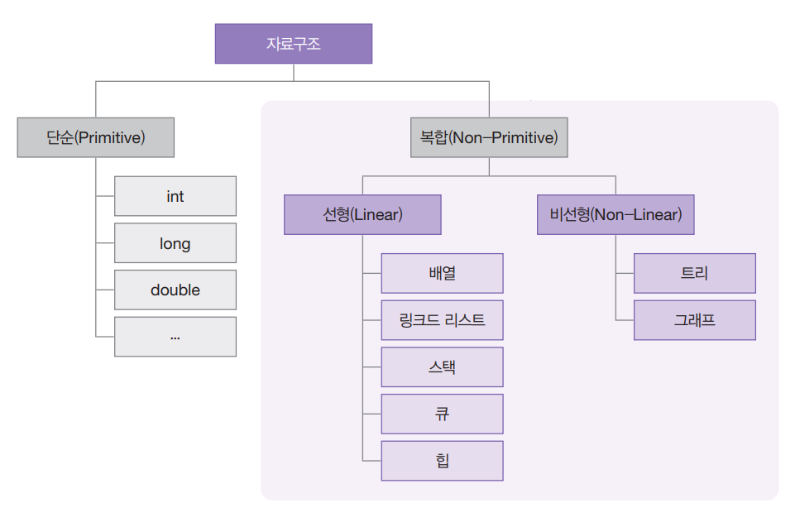
이진 탐색 트리(Binary Search Tree, BST)

구축

설계

이진 트리란 자식 노드가 최대 2개인 트리를 말한다.

이진 탐색 트리는 기준이 되는 노드(부모 노드)와 삽입하려는 데이터의 크기를 따져 작으면 왼쪽 자식 위치(left), 크거나 같으면 오른쪽 자식 위치(right)에 배치하는 정렬 방식을 따른다.

이러한 특징을 고려하여 BST 구축 전 💡Key Idea 를 설정하였다.

1. 삽입하려는 값이
   -> 기준 노드(부모 노드)보다 크기가 작으면 왼쪽(left) 자식 노드 생성
   -> 기준 노드(부모 노드)보다 크기가 같거나 크면 오른쪽(right) 자식 노드 생성

2. 다만, 이미 생성하려는 자식 노드 위치에 이미 값이 존재할 경우 새로운 노드 구조를 생성하도록 한다.
   기존 자식 노드가 새로운 부모 노드가 되어 자식 노드를 작성해 나가는 것이다.

코드

# 노드 클래스
class Node:
    def __init__(self, key):  # 생성자
        self.parent = key
        self.left = None
        self.right = None


# 이진 탐색 트리(BST) 클래스
class BST:
    def __init__(self):  # 생성자
        self.root = None

    # BST 구축
    def insert(self, key):
        if not self.root:
            self.root = Node(key)
        else:
            cur = self.root

            while True:
                if key < cur.parent:  # 기준 노드(부모 노드)보다 크기가 작으면 왼쪽(left) 자식 노드 생성
                    if cur.left:
                        cur = cur.left
                    else:
                        cur.left = Node(key)
                        break
                else:
                    if cur.right:  # 기준 노드(부모 노드)보다 크기가 같거나 크면 오른쪽(right) 자식 노드 생성
                        cur = cur.right
                    else:
                        cur.right = Node(key)
                        break


def solution(node_list):
    bst = BST()

    for key in node_list:
        bst.insert(key)

테스트

• Input

def main():
    # 테스트 케이스 1
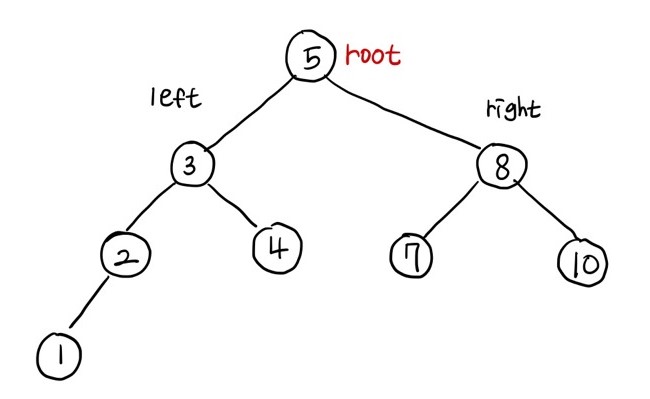
    solution([5, 3, 8, 4, 2, 1, 7, 10])


if __name__ == "__main__":
    main()

• 결과
  디버깅을 돌려보면, 다음과 같이 BST 구조가 정상적으로 구현되었음을 알 수 있다.
  

직접 디버깅을 돌려가며 BST가 구축되는 과정을 확인해보는 것을 추천한다.

디버깅 툴로는 구조가 한 눈에 파악이 되지 않으므로 구축한 트리 구조를 그림으로 표현해 보았다.

탐색

코드

class BST:
   
   ...

    # BST 탐색
    def search(self, key):
        cur = self.root

        # 노드가 존재하지 않거나 key = 현재 노드일 경우 loop 탈출
        # 탐색 값이 기준 노드 보다 작을 경우 왼쪽 자식 노드, 같거나 클 경우 오른쪽 자식 노드로 내려가 탐색
        while cur and cur.parent != key:
            if key < cur.parent:
                cur = cur.left
            else:
                cur = cur.right

        if cur:
            return cur.parent  # BST를 탐색하여 key 값과 일치하는 노드를 return
        else:
            return False  # 존재하지 않을 경우 False return


def solution(node_list, search_val):
    bst = BST()

    # 구축
    for key in node_list:
        bst.insert(key)

    # 탐색
    return bst.search(search_val)

테스트

• Input

def main():
    # 테스트 케이스 1
    print(solution([5, 3, 8, 4, 2, 1, 7, 10], 5))
    # 테스트 케이스 2
    print(solution([5, 3, 8, 4, 2, 1, 7, 10], 6))


if __name__ == "__main__":
    main()

• 결과
  

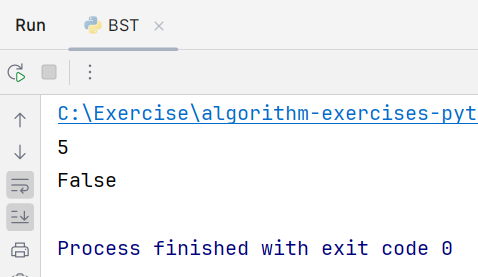
BST 탐색이 정상적으로 이루어지는지 확인하기 위해 두개의 테스트 케이스를 사용하였다.
만약 트리 내에 key 값(찾으려는 값)과 일치하는 노드를 찾는다면 해당 노드 값을 return 하도록 한다.
트리 내에 key 값이 존재하지 않으면 False를 return 하도록 하였다.

5 : 트리 내에 존재 하므로 5를 return
6 : 트리 내에 존재하지 않으므로 False를 return

최종 코드

# 트리 - 이진 탐색 트리(Binary Search Tree, BST) 구축/탐색

# 노드 클래스
class Node:
    def __init__(self, key):  # 생성자
        self.parent = key
        self.left = None
        self.right = None


# 이진 탐색 트리(BST) 클래스
class BST:
    def __init__(self):  # 생성자
        self.root = None

    # BST 구축
    def insert(self, key):
        if not self.root:
            self.root = Node(key)
        else:
            cur = self.root

            while True:
                if key < cur.parent:  # 기준 노드(부모 노드)보다 크기가 작으면 왼쪽(left) 자식 노드
                    if cur.left:
                        cur = cur.left
                    else:
                        cur.left = Node(key)
                        break
                else:
                    if cur.right:  # 기준 노드(부모 노드)보다 크기가 같거나 크면 오른쪽(right) 자식 노드
                        cur = cur.right
                    else:
                        cur.right = Node(key)
                        break

    # BST 탐색
    def search(self, key):
        cur = self.root

        # 노드가 존재하지 않거나 key = 현재 노드일 경우 loop 탈출
        # 탐색 값이 기준 노드 보다 작을 경우 왼쪽 자식 노드, 같거나 클 경우 오른쪽 자식 노드로 내려가 탐색
        while cur and cur.parent != key:
            if key < cur.parent:
                cur = cur.left
            else:
                cur = cur.right

        if cur:
            return cur.parent  # BST를 탐색하여 key 값과 일치하는 노드를 return
        else:
            return False  # 존재하지 않을 경우 False return


def solution(node_list, search_val):
    bst = BST()

    # 구축
    for key in node_list:
        bst.insert(key)

    # 탐색
    return bst.search(search_val)


def main():
    # 테스트 케이스 1
    print(solution([5, 3, 8, 4, 2, 1, 7, 10], 5))
    # 테스트 케이스 2
    print(solution([5, 3, 8, 4, 2, 1, 7, 10], 6))


if __name__ == "__main__":
    main()