[자료구조] 힙, heapify함수, 힙정렬, 우선순위 큐

soyyeong·2023년 9월 17일

자료구조 코테스터디

알고리즘

목록 보기

10/20

힙이란?

힙은 두 개의 조건을 만족하는 트리이다.

1. 형태 속성

힙은 완전 이진트리이다.
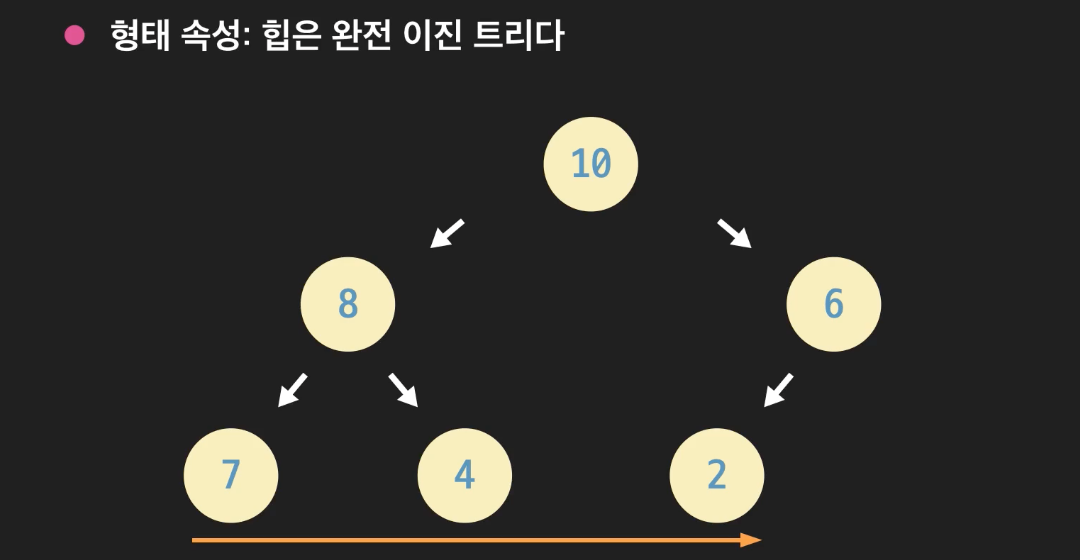
완전 이진트리의 중요한 특징으로 노드 개수가 n일 때 높이는 O(logn)이라는 점이다.

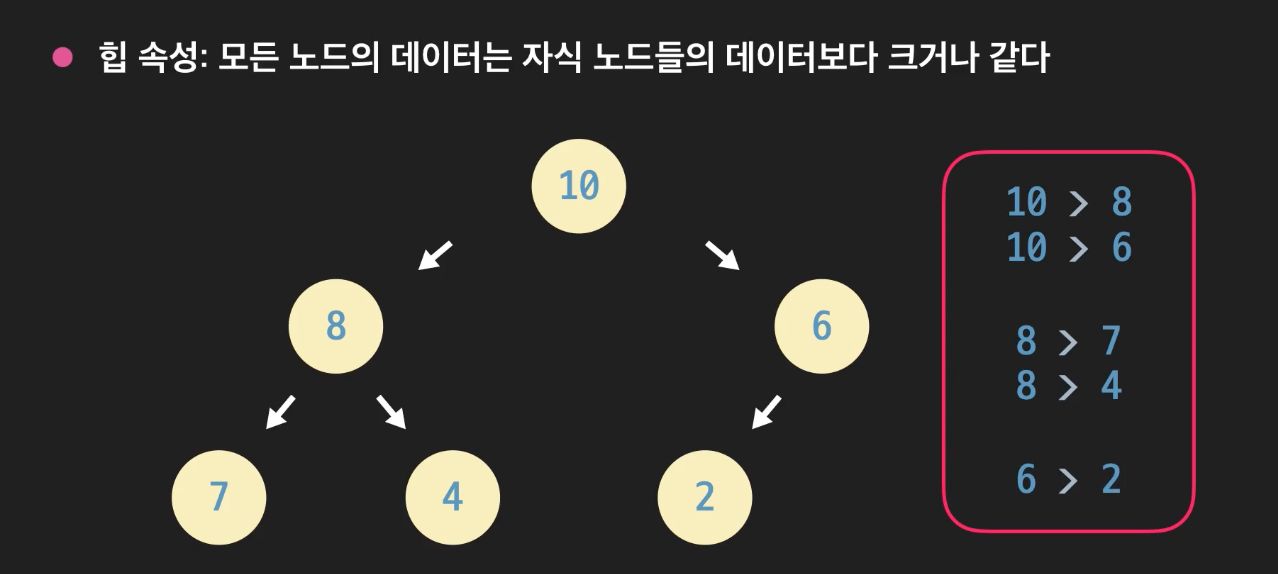
2. 힙 속성

모든 노드의 데이터는 자식 노드들의 데이터보다 크거나 같다.

힙을 활용하여 정렬문제, 우선순위 큐를 구현해보자.

정렬문제

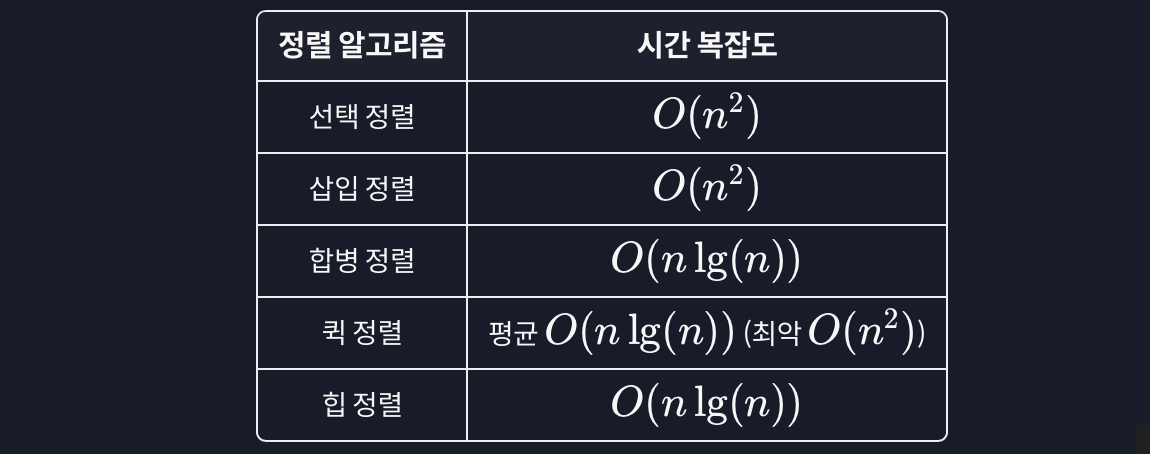
정렬 알고리즘 : 데이터를 재배치하는 구체적인 방법
- ex. 선택정렬, 삽입정렬, 합병정렬, 퀵정렬

배열로 구현한 힙

완전이진트리는 동적배열, 파이썬에서는 자료형 리스트를 이용해 나타낼 수 있다.
힙도 완전이진트리이기 때문에 동적배열로 나타낸다.

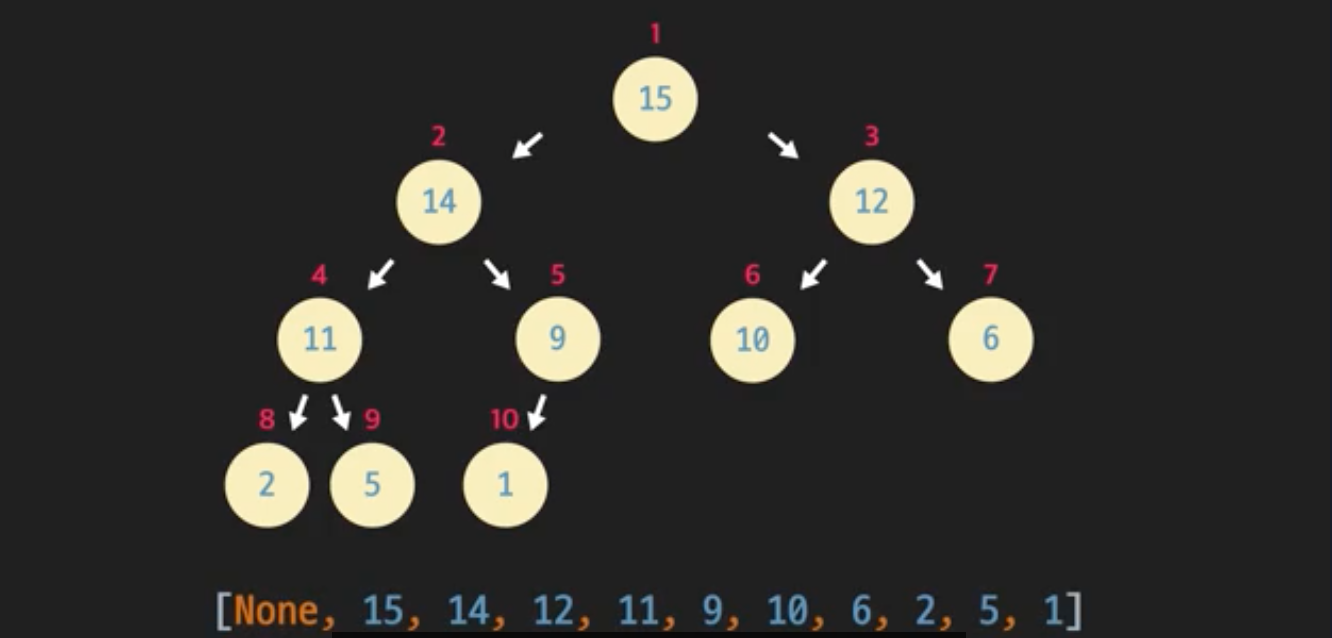
아래처럼 형태속성과 힙속성을 만족하는 힙을 파이썬 리스트로 나타내면 [None, 15, 14, 12, 11, 9, 10, 6, 2, 5, 1]이렇게 나타낼 수 있다. 내림차순으로 정렬된 리스트인 것을 확인할 수 있다.
노드 위에 빨간색 숫자는 인덱스를 나타내는데,
왼쪽 자식의 인덱스는 $인덱스 \times 2$ ,
오른쪽 자식 인덱스는 $인덱스 \times 2 +1$ 로 찾을 수 있다.

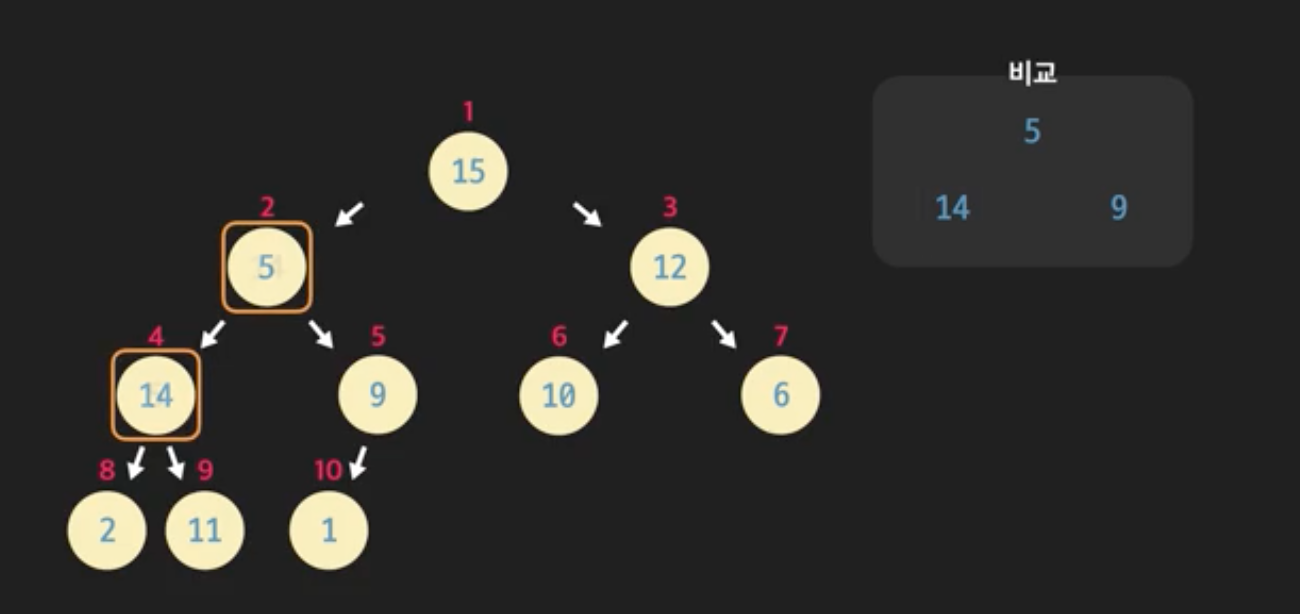
힙 만들기

아래 완전이진트리를 살펴보자. 형태속성은 만족하나, 부모노드 2가 자식노드 4보다 작은 수를 가지고 있어 힙속성은 만족하지 않는다. 이런 경우, 두 노드를 바꿔준다. 마찬가지로 힙 속성을 만족할 때까지 부모노드와 자식노드를 바꿔줌으로써 정렬문제를 해결할 수 있다. 이런 알고리즘을 heapify 라고 한다.

시간복잡도
힙은 완전이진트리이기 때문에 높이인 $O(logn)$ 에 비례하는 시간 복잡도를 가진다.

heapify 함수 구현

heapify 함수를 구현해보자

실습 설명
heapify() 함수는 아래 세 가지 파라미터를 받습니다.

완전 이진 트리를 나타내는 리스트, tree

heapify 하려는 노드의 인덱스, index

트리로 사용하는 리스트의 길이, tree_size (배열의 0번째 인덱스는 None으로 설정했기 때문에 실제로 총 노드 수보다 1이 큽니다.)
그리고 파라미터로 받은 tree의 index번째 노드가, 힙 속성을 유지하도록 트리 안의 노드들을 재배치합니다. (앞으로 “index" 번째 노드는 그냥 줄여서 “노드 index"라고 하겠습니다.)

heapify() 함수가 이런 기능을 하려면 아래와 같은 상세 작업을 순서대로 해야 합니다.
부모 노드(heapify하려는 현재 노드), 왼쪽 자식 노드, 오른쪽 자식 노드, 이 3가지 노드 중에서 가장 큰 값을 가진 노드가 무엇인지 파악합니다.
(1)가장 큰 값을 가진 노드가 부모 노드라면 그 상태 그대로 둡니다.
(2)가장 큰 값을 가진 노드가 자식 노드 중에 있다면 그 자식 노드와 부모 노드의 위치를 바꿔 줍니다. 기존의 부모 노드가 자식 노드로 내려갔을 때, 다시 힙 속성을 어길 수도 있습니다. 힙 속성이 충족될 때까지 1~2 단계를 반복합니다.
이때 단계 2-(2)를 보면 heapify() 함수 내에는 두 노드의 위치를 바꿀 수 있는 기능이 필요하다는 걸 알 수 있습니다. 이런 기능을 하는 swap() 이라는 함수를 미리 작성해 뒀는데요. swap() 함수는 아래 두 가지 파라미터를 받습니다.
리스트로 구현한 완전 이진 트리, tree 두 인덱스, index_1과 index_2
그리고 트리 내에서 두 인덱스에 해당하는 두 노드의 위치를 바꿔주죠. heapify() 함수의 내부 코드를 작성할 때 swap() 함수를 사용해 보세요.

실습결과
[None, 15, 14, 12, 11, 9, 10, 6, 2, 5, 1]

내가 쓴 코드

def swap(tree, index_1, index_2):
    """완전 이진 트리의 노드 index_1과 노드 index_2의 위치를 바꿔준다"""
    temp = tree[index_1]
    tree[index_1] = tree[index_2]
    tree[index_2] = temp


def heapify(tree, index, tree_size):
    """heapify 함수"""

    
    while (index < tree_size)&(2*index+1 < tree_size):
        # 왼쪽 자식 노드의 인덱스와 오른쪽 자식 노드의 인덱스를 계산
        left_child_index = 2 * index
        right_child_index = 2 * index + 1
        
        if (tree[left_child_index] > tree[index])&(tree[left_child_index] > tree[right_child_index]):
            swap(tree, left_child_index, index)
        elif (tree[right_child_index] > tree[index])&(tree[right_child_index] > tree[left_child_index]):
            swap(tree, right_child_index, index)
        index *= 2
        
    return tree

# 테스트 코드
tree = [None, 15, 5, 12, 14, 9, 10, 6, 2, 11, 1]  # heapify하려고 하는 완전 이진 트리
heapify(tree, 2, len(tree))  # 노드 2에 heapify 호출
print(tree)

나는 while 문으로 자식 노드까지 가게 했고, 해설에서는 재귀함수를 사용했다.

해설코드

def heapify(tree, index, tree_size):
    """heapify 함수"""

    # 왼쪽 자식 노드의 인덱스와 오른쪽 자식 노드의 인덱스를 계산
    left_child_index = 2 * index
    right_child_index = 2 * index + 1

    largest = index  # 일단 부모 노드의 값이 가장 크다고 설정

    # 왼쪽 자식 노드의 값과 비교
    if 0 < left_child_index < tree_size and tree[largest] < tree[left_child_index]:
        largest = left_child_index

    # 오른쪽 자식 노드의 값과 비교
    if 0 < right_child_index < tree_size and tree[largest] < tree[right_child_index]:
        largest = right_child_index
    
    if largest != index: # 부모 노드의 값이 자식 노드의 값보다 작으면
        swap(tree, index, largest)  # 부모 노드와 최댓값을 가진 자식 노드의 위치를 바꿔준다
        heapify(tree, largest, tree_size)  # 자리가 바뀌어 자식 노드가 된 기존의 부모 노드를대상으로 또 heapify 함수를 호출한다

이번엔 인덱스 뒤에서부터 차례대로 heapify를 하면 heap을 만들 수 있다. 이때 걸리는 시간은 $O(nlogn)$ 이다.

힙 정렬

이번에는 heapify를 이용해서 힙 정렬을 하는 법을 알아보자.

힙을 만든다.

root와 마지막 노드를 바꿔준다.

바꾼 노드는 트리에서 없는 취급한다.

새로운 노드가 힙 속성을 지킬 수 있게 heapify를 호출한다.
(모든 인덱스를 돌 때까지 반복한다)

def swap(tree, index_1, index_2):
    """완전 이진 트리의 노드 index_1과 노드 index_2의 위치를 바꿔준다"""
    temp = tree[index_1]
    tree[index_1] = tree[index_2]
    tree[index_2] = temp


def heapify(tree, index, tree_size):
    """heapify 함수"""

    # 왼쪽 자식 노드의 인덱스와 오른쪽 자식 노드의 인덱스를 계산
    left_child_index = 2 * index
    right_child_index = 2 * index + 1

    largest = index  # 일단 부모 노드의 값이 가장 크다고 설정

    # 왼쪽 자식 노드의 값과 비교
    if 0 < left_child_index < tree_size and tree[largest] < tree[left_child_index]:
        largest = left_child_index

    # 오른쪽 자식 노드의 값과 비교
    if 0 < right_child_index < tree_size and tree[largest] < tree[right_child_index]:
        largest = right_child_index
    
    if largest != index: # 부모 노드의 값이 자식 노드의 값보다 작으면
        swap(tree, index, largest)  # 부모 노드와 최댓값을 가진 자식 노드의 위치를 바꿔준다
        heapify(tree, largest, tree_size)  # 자리가 바뀌어 자식 노드가 된 기존의 부모 노드를대상으로 또 heapify 함수를 호출한다

def heapsort(tree):
    """힙 정렬 함수"""
    tree_size = len(tree)
    if tree_size <= 2:
      return tree
    # 1. 마지막 노드부터 root 노드까지 heapify를 해준다 
    for index in range(tree_size-1, 0, -1):
      heapify(tree, index, tree_size)

    # 2.
    # 마지막 인덱스부터 처음 인덱스까지
    for i in range(tree_size-1, 0, -1):
        swap(tree, 1, i)  # root 노드와 마지막 인덱스를 바꿔준 후
        heapify(tree, 1, i)  # root 노드에 heapify를 호출한다


# 테스트 코드
data_to_sort = [None, 6, 1, 4, 7, 10, 3, 8, 5, 1, 5, 7, 4, 2, 1]
heapsort(data_to_sort)
print(data_to_sort)


# 테스트 코드
data_to_sort = [None, 6, 1, 4, 7, 10, 3, 8, 5, 1, 5, 7, 4, 2, 1]
heapsort(data_to_sort)

힙정렬 시간복잡도

힙을 만드는 데 $O(nlg(n))$
만든 힙에서 매번 root 노드를 뽑고 남은 걸 다시 힙으로 만드는 작업 반복하는 데 $O(nlg(n))$

힙정렬의 총 시간 복잡도는 $O(nlg(n)+nlg(n)) = O(2nlg(n))$ 이고, 시간복잡도에서 상수는 무시되니, 결국 $O(nlg(n))$ 이라고 할 수 있다.

우선순위 큐

앞서 힙을 사용해서 정렬과 우선순위 큐를 만들 수 있다고 언급했다.

우선순위 큐는 추상 자료형이다.
- 추상 자료형 : 내부적인 구현보다 기능에 집중하게 해주는 개념
- 큐 : 먼저 들어간 데이터가 먼저 나오는 자료형
우선순위 큐
- 힙을 이용하면 우선순위 큐를 효율적으로 구현할 수 있다.
- 데이터를 저장할 수 있다.
- 저장한 데이터가 우선순위 순서대로 나온다.
힙으로 우선순위 큐를 구현하기 위해서는 힙에 데이터를 삽입하고 또 삭제하는 방법을 알아야 한다.
힙에 데이터 삽입하기
- 힙의 마지막 인덱스에 데이터를 삽입한다.
- 삽입한 데이터와 부모 노드의 데이터를 비교한다.
- 부모 노드의 데이터가 더 작으면 둘의 위치를 바꿔준다.
  (새로 삽입한 노드가 제 위치를 찾을 때까지 반복한다.)

힙에 데이터 삽입 구현하기

insert() 메소드로 데이터를 삽입할 때 이루어져야 하는 일을 순서대로 정리하면 아래의 3단계로 나눌 수 있습니다.
힙의 마지막 인덱스에 노드를 삽입합니다.
(1)삽입한 노드와 그 부모 노드를 비교해서 부모 노드가 더 작으면 둘의 위치를 바꿉니다. (2) 삽입한 노드와 그 부모 노드를 비교해서 부모 노드가 더 크면 그대로 둡니다.
2-(1)의 경우에는 삽입한 노드가 올바른 위치를 찾을 때까지 2 단계를 반복합니다.
이때 2 단계와 3 단계의 작업을 하는 별도의 함수 reverse_heapify()를 정의할게요.
reverse_heapify 함수는 다음과 같은 파라미터를 받습니다.
리스트로 구현한 완전 이진 트리, tree
삽입된 노드의 인덱스, index
그리고 삽입된 노드를 힙 속성을 유지할 수 있는 위치로 이동시킵니다.
이전에 배운 heapify() 함수가 위에 있는 노드를 아래로 이동시켜서 힙 속성을 유지했다면 reverse_heapify() 함수는 아래에 있는 노드를 위로 이동시켜서 힙 속성을 유지하는 거죠.

내가 쓴 코드

def swap(tree, index_1, index_2):
    """완전 이진 트리의 노드 index_1과 노드 index_2의 위치를 바꿔준다"""
    temp = tree[index_1]
    tree[index_1] = tree[index_2]
    tree[index_2] = temp


def reverse_heapify(tree, index):
    """삽입된 노드를 힙 속성을 지키는 위치로 이동시키는 함수"""
    # index : 삽입된 노드의 인덱스 (마지막 인덱스)
    parent_index = index // 2
    while parent_index > 0:
        if 0<index<len(tree) and tree[index] > tree[parent_index]:
            swap(tree, index, parent_index)
            index = index//2 
            parent_index = parent_index//2 
        else:
            return tree
            
class PriorityQueue:
    """힙으로 구현한 우선순위 큐"""
    def __init__(self):
        self.heap = [None]  # 파이썬 리스트로 구현한 힙


    def insert(self, data):
        """삽입 메소드"""
        self.heap.append(data)
        reverse_heapify(self.heap, len(self.heap)-1)


    def __str__(self):
        return str(self.heap)


# 테스트 코드
priority_queue = PriorityQueue()

priority_queue.insert(6)
priority_queue.insert(9)
priority_queue.insert(1)
priority_queue.insert(3)
priority_queue.insert(10)
priority_queue.insert(11)
priority_queue.insert(13)

print(priority_queue)

해설코드
: 재귀함수를 썼다. 이게 더 낫다!

def reverse_heapify(tree, index):
    """삽입된 노드를 힙 속성을 지키는 위치로 이동시키는 함수"""
    parent_index = index // 2  # 삽입된 노드의 부모 노드의 인덱스 계산

    # 부모 노드가 존재하고, 부모 노드의 값이 삽입된 노드의 값보다 작을 때
    if 0 < parent_index < len(tree) and tree[index] > tree[parent_index]:
        swap(tree, index, parent_index)  # 부모 노드와 삽입된 노드의 위치 교환
        reverse_heapify(tree, parent_index)  # 삽입된 노드를 대상으로 다시 reverse_heapify 호출

힙에서 최고 우선순위 데이터 추출하기

힙에서 가장 큰 값을 추출하고 싶은 경우 (힙에서 root 노드 데이터 추출하기)
- root 노드와 마지막 노드를 서로 바꿔 준다.
- 마지막 노드의 데이터를 변수에 저장해 준다.
- 마지막 노드를 삭제한다.
- root노드에 heapify를 호출해서 망가진 힙 속성을 고친다.

def swap(tree, index_1, index_2):
    """완전 이진 트리의 노드 index_1과 노드 index_2의 위치를 바꿔 준다"""
    temp = tree[index_1]
    tree[index_1] = tree[index_2]
    tree[index_2] = temp


def heapify(tree, index, tree_size):
    """heapify 함수"""

    # 왼쪽 자식 노드의 인덱스와 오른쪽 자식 노드의 인덱스를 계산
    left_child_index = 2 * index
    right_child_index = 2 * index + 1

    largest = index  # 일단 부모 노드의 값이 가장 크다고 설정

    # 왼쪽 자식 노드의 값과 비교
    if 0 < left_child_index < tree_size and tree[largest] < tree[left_child_index]:
        largest = left_child_index

    # 오른쪽 자식 노드의 값과 비교
    if 0 < right_child_index < tree_size and tree[largest] < tree[right_child_index]:
        largest = right_child_index
    
    if largest != index: # 부모 노드의 값이 자식 노드의 값보다 작으면
        swap(tree, index, largest)  # 부모 노드와 최댓값을 가진 자식 노드의 위치를 바꿔 준다
        heapify(tree, largest, tree_size)  # 자리가 바뀌어 자식 노드가 된 기존의 부모 노드를대상으로 또 heapify 함수를 호출한다


def reverse_heapify(tree, index):
    """삽입된 노드를 힙 속성을 지키는 위치로 이동시키는 함수"""
    parent_index = index // 2  # 삽입된 노드의 부모 노드의 인덱스 계산

    # 부모 노드가 존재하고, 부모 노드의 값이 삽입된 노드의 값보다 작을 때
    if 0 < parent_index < len(tree) and tree[index] > tree[parent_index]:
        swap(tree, index, parent_index)  # 부모 노드와 삽입된 노드의 위치 교환
        reverse_heapify(tree, parent_index)  # 삽입된 노드를 대상으로 다시 reverse_heapify 호출        


class PriorityQueue:
    """힙으로 구현한 우선순위 큐"""
    def __init__(self):
        self.heap = [None]  # 파이썬 리스트로 구현한 힙

    def insert(self, data):
        """삽입 메소드"""
        self.heap.append(data)  # 힙의 마지막에 데이터 추가
        reverse_heapify(self.heap, len(self.heap)-1) # 삽입된 노드(추가된 데이터)의 위치를 재배치

    def extract_max(self):
        """최고 우선순위 데이터 추출 메소드"""
        swap(self.heap, 1, len(self.heap) - 1)  # root 노드와 마지막 노드의 위치 바꿈
        max_value = self.heap.pop()  # 힙에서 마지막 노드 추출(삭제)해서 변수에 저장
        heapify(self.heap, 1, len(self.heap))  # 새로운 root 노드를 대상으로 heapify 호출해서 힙 속성 유지
        return max_value  # 최우선순위 데이터 리턴

    def __str__(self):
        return str(self.heap)
        
# 테스트 코드
priority_queue = PriorityQueue()

priority_queue.insert(6)
priority_queue.insert(9)
priority_queue.insert(1)
priority_queue.insert(3)
priority_queue.insert(10)
priority_queue.insert(11)
priority_queue.insert(13)

print(priority_queue.extract_max())
print(priority_queue.extract_max())
print(priority_queue.extract_max())
print(priority_queue.extract_max())
print(priority_queue.extract_max())
print(priority_queue.extract_max())
print(priority_queue.extract_max())