0️⃣ 알고리즘 패러다임
- 자주 나타나는 알고리즘 접근법
한 문제에도 다양한 솔루션이 존재하고, 여러 알고리즘 패러다임으로 문제를 풀 수 있다.
1️⃣ Brute Force (무차별 대입 공격)
- 무차별적으로 가능한 모든 대안(
경우의 수)을 시도해 보는 가장 순진한 알고리즘 접근법
Brute Force 예제
카드 두 뭉치가 있습니다.
왼쪽 뭉치에서 카드를 하나 뽑고 오른쪽 뭉치에서 카드를 하나 뽑아서, 두 수의 곱이 가장 크게 만들고 싶은데요. 어떻게 하면 가장 큰 곱을 구할 수 있을까요?
함수 max_product는 리스트 left_cards와 리스트 right_cards를 파라미터로 받습니다.
left_cards는 왼쪽 카드 뭉치의 숫자들, right_cards는 오른쪽 카드 뭉치 숫자들이 담겨 있고, max_product는 left_cards에서 카드 하나와 right_cards에서 카드 하나를 뽑아서 곱했을 때 그 값이 최대가 되는 값을 리턴합니다.
Brute Force 파이썬 풀이
def max_product(left_cards, right_cards):
product_list = []
for l in left_cards:
for r in right_cards:
product_list.append(l*r)
return max(product_list)
# 테스트 코드
print(max_product([1, 6, 5], [4, 2, 3]))
print(max_product([1, -9, 3, 4], [2, 8, 3, 1]))
print(max_product([-1, -7, 3], [-4, 3, 6]))시간 복잡도
len(left_cards)을 m, len(right_cards)을 n이라고 하면,left_cards를 도는 반복문 안에 right_cards를 도는 반복문이 중첩되어 있으니 max_product의 시간 복잡도는 O(mn)이다.
Brute Force의 장단점
이해하기 쉽고 올바른 답을 구할 것이라는 확신을 가질 수 있는 알고리즘이나, 모든 경우의 수를 본다는 것이 비효율적이고, 이 비효율은 인풋이 커질수록 훨씬 더 커진다.
그럼에도 Brute Force는 '직관적이고 명확하다'라는 큰 장점 덕분에 코드를 구현하기도 비교적 쉽고, 모든 경우를 본다는 것 때문에 답을 확실하게 찾을 수 있다. 더 효율적인 알고리즘을 찾기 위한 시작점으로 Brute Force를 생각해볼 수 있다.
2️⃣ Divide and Conquer (분할 정복)
- 답을 바로 알아내기 어려운(큰) 문제의 경우, 문제를 부분문제로 쪼개 나눠 해결하는 것으로, 아래와 같이 3가지로 나뉜다.
Divide: 문제를 부분문제로 나눈다.- f(X)를 풀기 전에 인풋 X를 x1, x2로 나눈다. (분할)
Conquer: 각 부분문제를 정복한다.- 부분문제 f(x1), f(x2) 를 만들어 솔루션 A, B을 구한다. (정복)
Combine: 부분문제들의 솔루션을 합쳐서 기존 문제를 해결한다.- 솔루션 A, B를 이용해 기존 문제를 해결하는 f(X)를 계산한다.
- 만약 쪼갠 부분문제 f(x1), f(x2)도 너무 큰 문제라면 이것도 Divide&Conquer 방식으로 풀어야 한다.따라서 문제가 충분히 작아질때까지 문제를 쪼개는데, 내부적으로 이렇게 복잡한 과정들이 일어난다는 점에서 재귀문제와 비슷하다고 할 수 있다.
Divide&Conquer 예제
Divide and Conquer를 이용해서 1부터 n까지 더하는 함수 consecutive_sum를 구현해보자. 두 개의 정수 인풋 start와 end를 받고, start부터 end까지의 합을 리턴한다. end는 start보다 크다고 가정한다.
Divide&Conquer 파이썬 풀이
def consecutive_sum(start, end):
if start == end :
return start
else:
s = start+end-1
return consecutive_sum(start, s//2) + consecutive_sum(s//2+1, end)
# 테스트 코드
print(consecutive_sum(1, 10))
print(consecutive_sum(1, 100))
print(consecutive_sum(1, 253))
print(consecutive_sum(1, 388))3️⃣ Merge Sort (합병정렬)
하나의 리스트를 두 개의 균등한 크기로 분할하고 분할된 부분 리스트를 정렬한 다음, 두 개의 정렬된 부분 리스트를 합하여 전체가 정렬된 리스트가 되게 하는 방법으로, 위에서 살펴본 Divide&Conquer방식을 사용한다.
Divide: 문제를 부분문제로 나눈다.- 리스트를 반으로 나눈다.
Conquer: 각 부분문제를 정복한다.- 왼쪽 리스트와 오른쪽 리스트를 각각 정렬한다.
Combine: 부분문제들의 솔루션을 합쳐서 기존 문제를 해결한다.- 정렬된 두 리스트를 하나의 정렬된 리스트로 합병한다.
즉, 작은 리스트로 나뉘어 정렬한 뒤에 이어붙이는 걸 반복하는 것이다.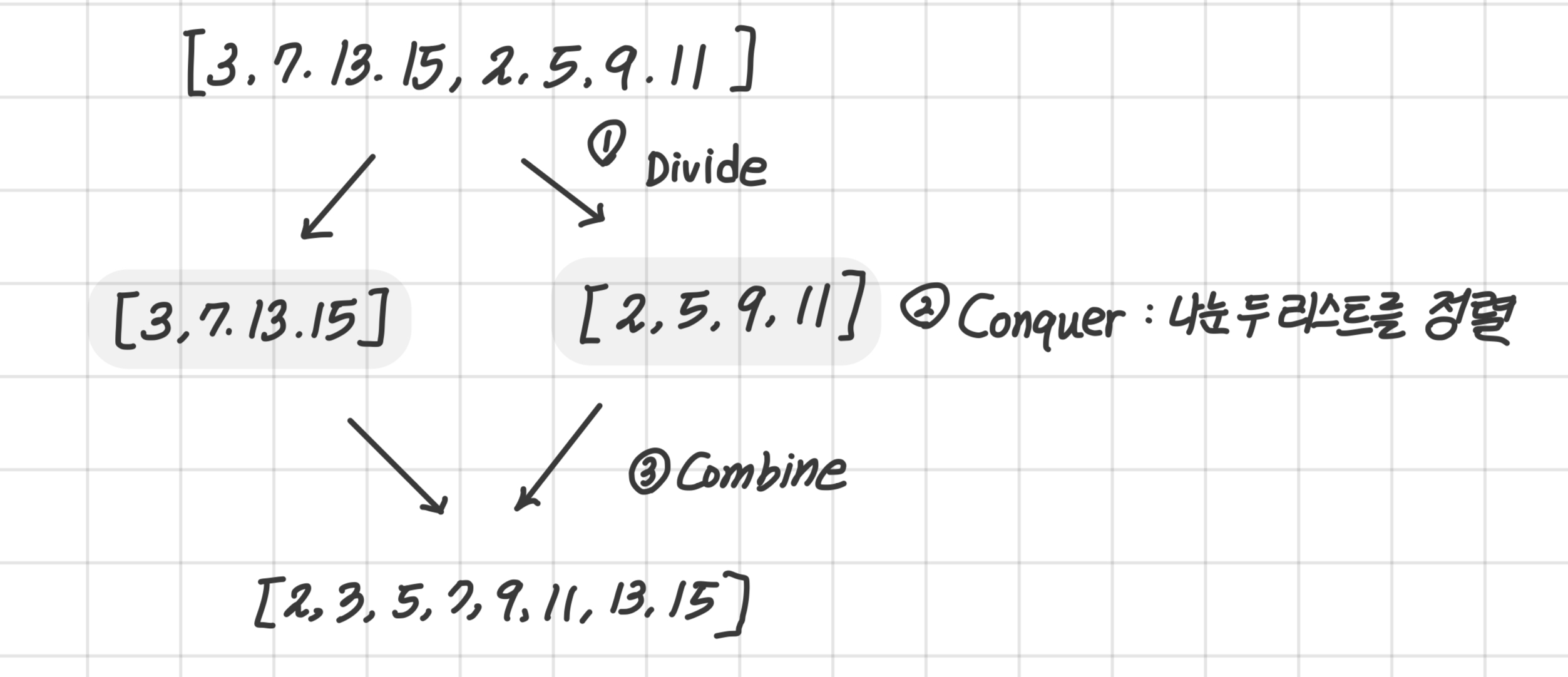
여기에서 중요하게 보아야 하는 부분이 Combine 부분인데, 이렇게 정렬된 두 개의 리스트를 그냥 합병하는 게 아니라, 왼쪽 리스트와 오른쪽 리스트의 첫번째 값인 3과 2중 더 작은 2가 먼저 들어간다. 그 이후에 왼쪽의 3과 오른쪽의 5를 비교하여 더 작은 3을 넣고, 7과 5를 비교하여 더 작은 5를 넣고.. 이런식으로 반복하여 정렬된 리스트를 만들 수 있다.
Merged Sort 예제 1
merge 함수는 정렬된 두 리스트 list1과 list2를 받아서, 하나의 정렬된 리스트를 리턴
Merged Sort 파이썬 풀이 1
def merge(list1, list2):
sorted_list = []
while list1 and list2: # 두 리스트 모두 비어있지 않은 동안에 루프
if list1[0] < list2[0]:
sorted_list.append(list1[0])
list1 = list1[1:]
else:
sorted_list.append(list2[0])
list2 = list2[1:]
sorted_list += list1 + list2 # 남은 건 추가하기
return sorted_list
# 테스트 코드
print(merge([1],[]))
print(merge([],[1]))
print(merge([2],[1]))
print(merge([1, 2, 3, 4],[5, 6, 7, 8]))
print(merge([5, 6, 7, 8],[1, 2, 3, 4]))
print(merge([4, 7, 8, 9],[1, 3, 6, 10]))Merged Sort 예제 2
Divide and Conquer 방식으로 merge_sort 함수를 써 보자. merge_sort는 파라미터로 리스트 하나를 받고, 정렬된 새로운 리스트를 리턴
Merged Sort 파이썬 풀이 2
def merge(list1, list2): # 위에서 본 두 리스트 정렬하면서 합치기
sorted_list = []
while list1 and list2:
if list1[0] < list2[0]:
sorted_list.append(list1[0])
list1 = list1[1:]
else:
sorted_list.append(list2[0])
list2 = list2[1:]
sorted_list += list1 + list2
return sorted_list
# 합병 정렬
def merge_sort(my_list):
if len(my_list) <= 1:
return my_list
else:
# my_list를 반씩 나눈다(divide)
idx = len(my_list)//2
# merge_sort 함수를 재귀적으로 호출하여 부분 문제 해결(conquer)하고,
left = merge_sort(my_list[:idx])
right = merge_sort(my_list[idx:])
# merge 함수로 정렬된 두 리스트를 합쳐(combine)준다
return merge(left, right)
# 테스트 코드
print(merge_sort([1, 3, 5, 7, 9, 11, 13, 11]))
print(merge_sort([28, 13, 9, 30, 1, 48, 5, 7, 15]))
print(merge_sort([2, 5, 6, 7, 1, 2, 4, 7, 10, 11, 4, 15, 13, 1, 6, 4]))4️⃣ QuickSort (퀵 정렬)
퀵 정렬도 Divide&Conquer방식을 사용하는 정렬이다. 합병정렬은 Divide, Conquer단계는 쉬웠던 반면 Combine 단계가 복잡하고, 퀵정렬은 Divide 단계에서 어렵고 Conquer, Combine 부분은 쉽다.
퀵 정렬에서 리스트를 나누는 과정은 파티션(Partition)이라고 부른다. 파티션은 다음 두 가지로 나뉜다.
파티션(Partition)
1. 리스트에서 pivot(기준점)을 정한다.
2. 이 피벗을 기준으로 더 작은 값은 모두 왼쪽으로, 더 큰 값은 모두 오른쪽으로 오게끔 한다.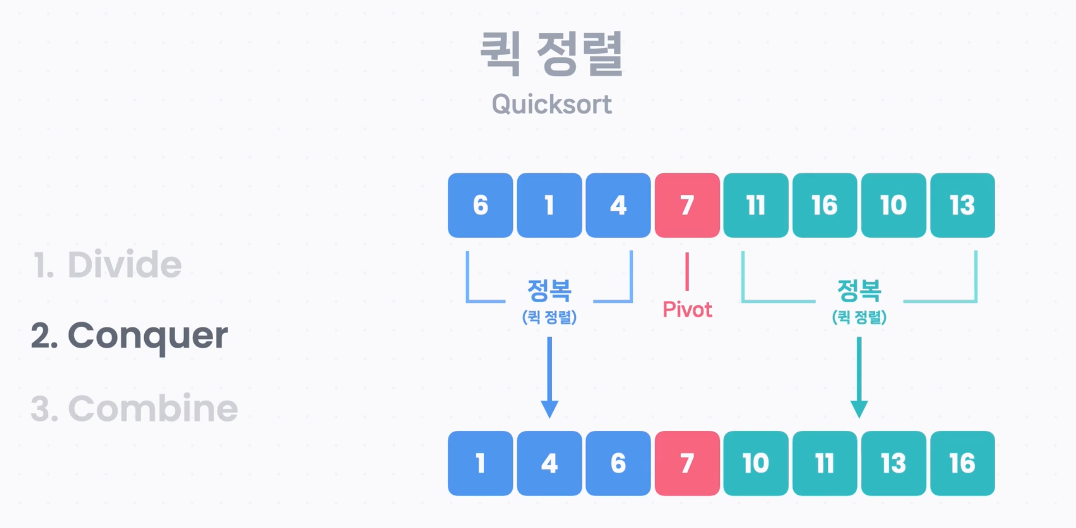
Divide:파티션(Partition)을 진행한다. 어떤 기준점(피봇, Pivot)을 정하고, 더 작은 요소는 왼쪽, 큰 값은 오른쪽에 오도록 한다.Conquer: 피봇의 왼쪽에 있는 값들과 오른쪽에 있는 값들을 각각 정렬한다.Combine: Divide, Conquer에서 이미 정렬되어 있어 할 일이 없다.
마찬가지로 왼쪽과 오른쪽에 있는 값들을 재귀적으로 정렬하면 된다. 앞서 Divide과정인 파티션이 복잡하다고 했는데, 파티션을 구현하는 방법을 알아보자.
기준점을 정해서, 더 작은 값은 왼쪽, 더 큰 값은 모두 오른쪽에 오도록 하는 가장 쉽게 생각할 수 있는 방법은 아래처럼 값을 하나씩 비교해서 왼쪽(small)에 들어올 값의 리스트, 오른쪽(big)에 올 값의 리스트를 만드는 거다.
def partition(my_list):
pivot = my_list.pop()
small=[]
big=[]
for num in my_list:
if num > pivot:
big.append(num)
else:
small.append(num)
return small + [pivot] + big나도 이 방법을 먼저 생각했는데, 코드잇 강의에서는 다른 방법을 사용했다. 이 방법이 직관적이고 쉬운데 다른 방법을 사용하는 이유가 궁금했고, 역시나 같은 질문이 올라와 있었다. 그 질문에 대한 답변은 아래와 같다. 
그래서 강의에서 소개한 파티션(Partition) 방법은 이렇게 진행된다.
pivot으로 맨 왼쪽에 있는 수를 정하고, 아래처럼 정렬되도록 변경하는 거다.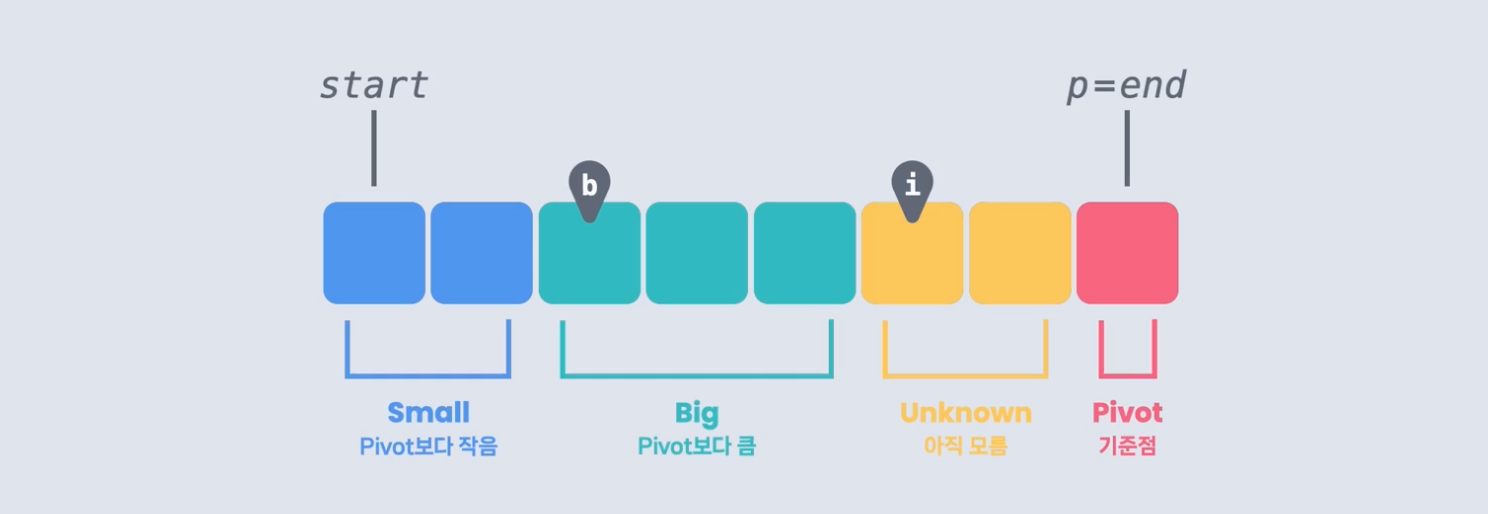
pivot보다 작은 수, pivot보다 큰 수(Big), 아직 모르는 수 순서대로 수를 옮기게 된다.
여기서 p는 피봇의 인덱스, b는 Big 수들의 첫 번째 인덱스, i는 아직 모르는 수들의 첫 번째 인덱스이다.
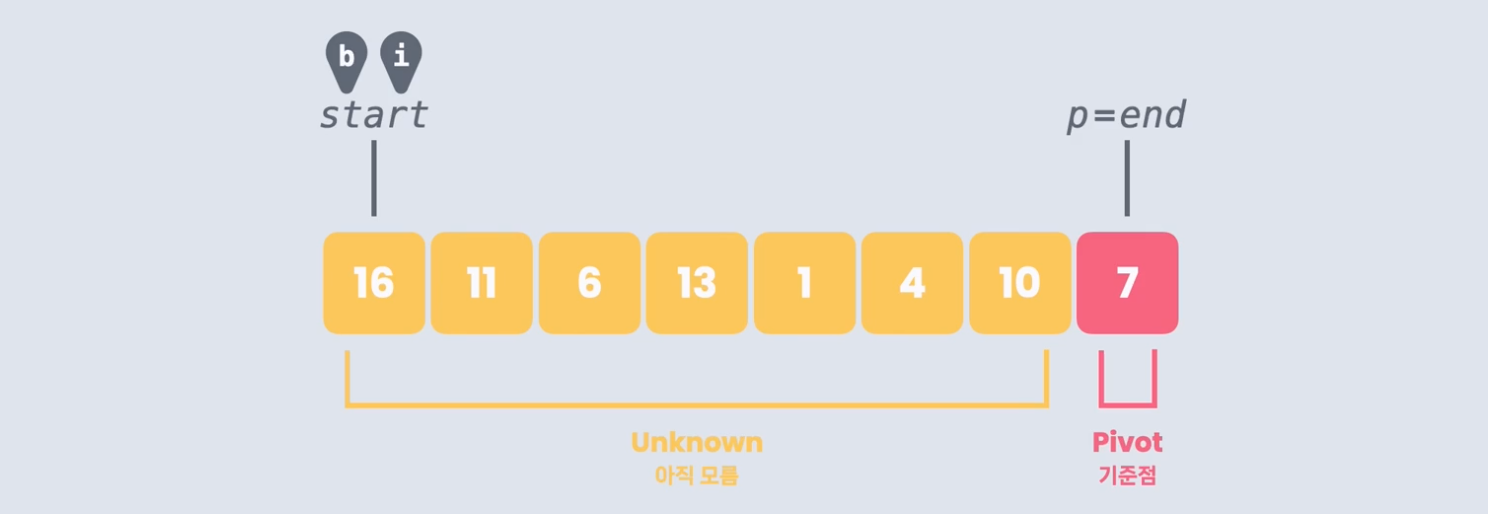
맨 처음 b,i는 0번 인덱스를 가리킨다.
이제 i를 한 칸씩 앞으로 이동하면서 하나씩 비교해 갈 거다.
16과 7을 비교해서 16이 크니까 b는 이동하지 않고, i는 한 칸 이동하여 11을 가리킨다. 11도 마찬가지로 진행한다.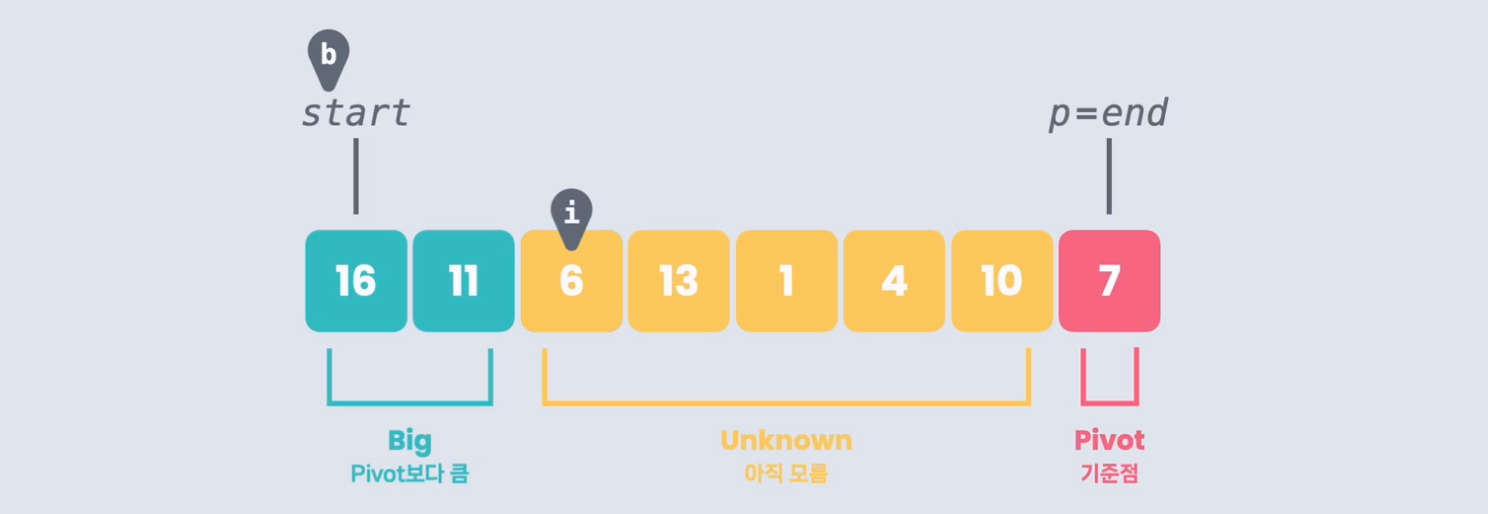
이번에 6과 7을 비교하는데 6은 small그룹에 들어가야 하니까, 앞으로 보내야 한다. 앞으로 보내기 위해 b가 가리키는 16과 i가 가리키는 6의 자리를 바꾸고, b와 i를 모두 한 칸씩 오른쪽으로 옮긴다.
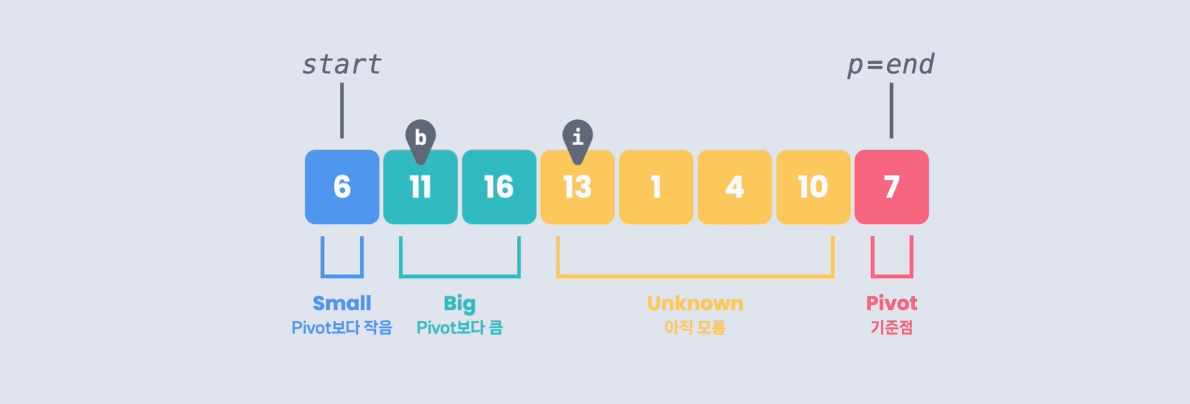
이런 방식을 반복하여 i가 p위치로 갈때까지 진행한다.
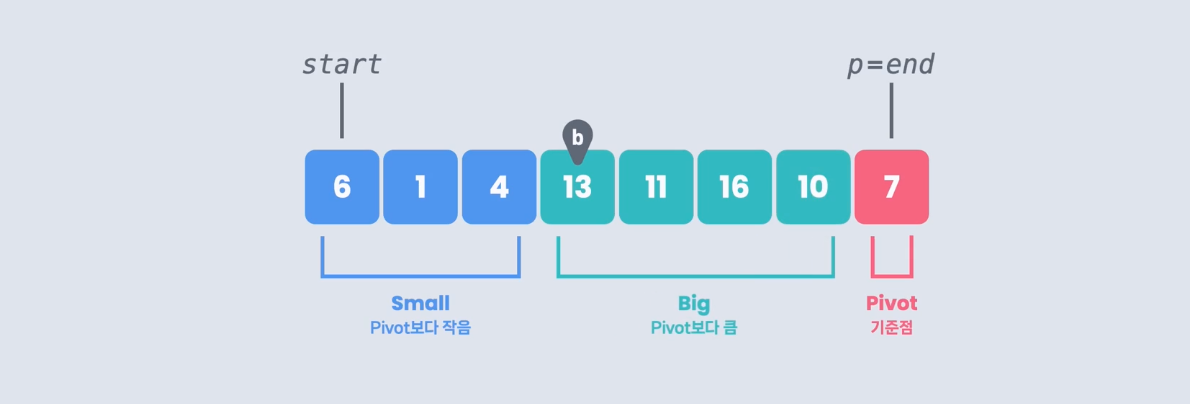
그럼 이렇게 small, big, pivot 순으로 정리가 되는데, pivot이 small그룹과 big 그룹의 사이에 있어야 하므로, b와 p의 자리에 있는 13과 7을 바꿔준다.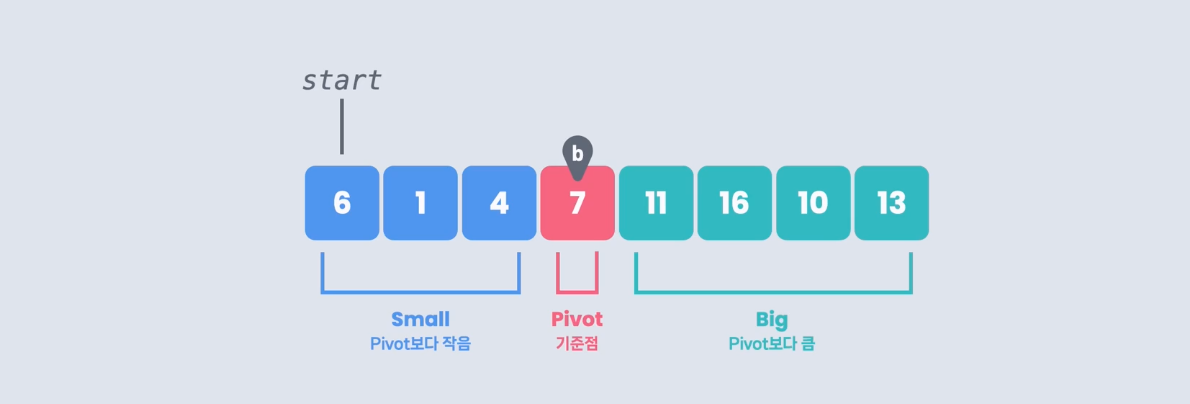
그럼 최종적으로 pivot을 기준으로 왼쪽에는 small그룹, 오른쪽에는 Big그룹이 있도록 하는 Partition을 구현할 수 있다. 이걸 코드로 한 번 구현해보자.
QuickSort Partition 함수 구현
# 두 요소의 위치를 바꿔주는 helper function
def swap_elements(my_list, index1, index2):
my_list[index1], my_list[index2] = my_list[index2], my_list[index1]
# 퀵 정렬에서 사용되는 partition 함수
def partition(my_list, start, end):
p, b, i = end, 0, 0
while i < p:
if my_list[i] <= my_list[p]:
swap_elements(my_list, i, b)
b += 1
i += 1
swap_elements(my_list, b, p)
return b
# 테스트 코드 1
list1 = [4, 3, 6, 2, 7, 1, 5]
pivot_index1 = partition(list1, 0, len(list1) - 1)
print(list1)
print(pivot_index1)
# 테스트 코드 2
list2 = [6, 1, 2, 6, 3, 5, 4]
pivot_index2 = partition(list2, 0, len(list2) - 1)
print(list2)
print(pivot_index2)QuickSort 구현
Divide and Conquer 방식으로 quicksort 함수를 구현해보자.
merge_sort 함수와 달리 quicksort 함수는 정렬된 새로운 리스트를 리턴하는 게 아니라, 파라미터로 받는 리스트 자체를 정렬시키는 것입니다.
# 두 요소의 위치를 바꿔주는 helper function
def swap_elements(my_list, index1, index2):
my_list[index1], my_list[index2] = my_list[index2], my_list[index1]
# 퀵 정렬에서 사용되는 partition 함수
def partition(my_list, start, end):
p, b, i = end, 0, 0
while i < p:
if my_list[i] <= my_list[p]:
swap_elements(my_list, i, b)
b += 1
i += 1
swap_elements(my_list, b, p)
return b
# 퀵 정렬 (start, end 파라미터 없이도 호출이 가능하도록 수정해보세요!)
def quicksort(my_list, start=0, end=None):
if end == None:
end = len(my_list) -1
if end - start < 1:
return
pivot = partition(my_list, start, end)
quicksort(my_list, start, pivot - 1)
quicksort(my_list, pivot + 1, end)
# 테스트 코드 1
list1 = [1, 3, 5, 7, 9, 11, 13, 11]
quicksort(list1) # start, end 파라미터 없이 호출
print(list1)
# 테스트 코드 2
list2 = [28, 13, 9, 30, 1, 48, 5, 7, 15]
quicksort(list2) # start, end 파라미터 없이 호출
print(list2)
# 테스트 코드 3
list3 = [2, 5, 6, 7, 1, 2, 4, 7, 10, 11, 4, 15, 13, 1, 6, 4]
quicksort(list3) # start, end 파라미터 없이 호출
print(list3)