0️⃣ Dynamic Programming 의 필요 조건
🔎 1. 최적 부분 구조 (Optimal Substructure)
- '최적 부분 구조가 있다'는 건 "부분 문제들의 최적의 답을 이용해서 기존 문제의 최적의 답을 구할 수 있다는 것"을 의미한다.
예시1. 피보나치 수
다섯번째 피보나치 수를 구하기 위해서는 네 번째 피보나치 수와 세 번째 피보나치 수를 구하는 부분문제를 먼저 해결해야 한다. 이 두 부분문제의 최적의 답을 구하면, 기존문제(다섯번째 피보나치 수)의 최적의 답을 구할 수 있다.
따라서 피보나치 수는 '최적부분구조를 가지고 있다'고 표현한다.
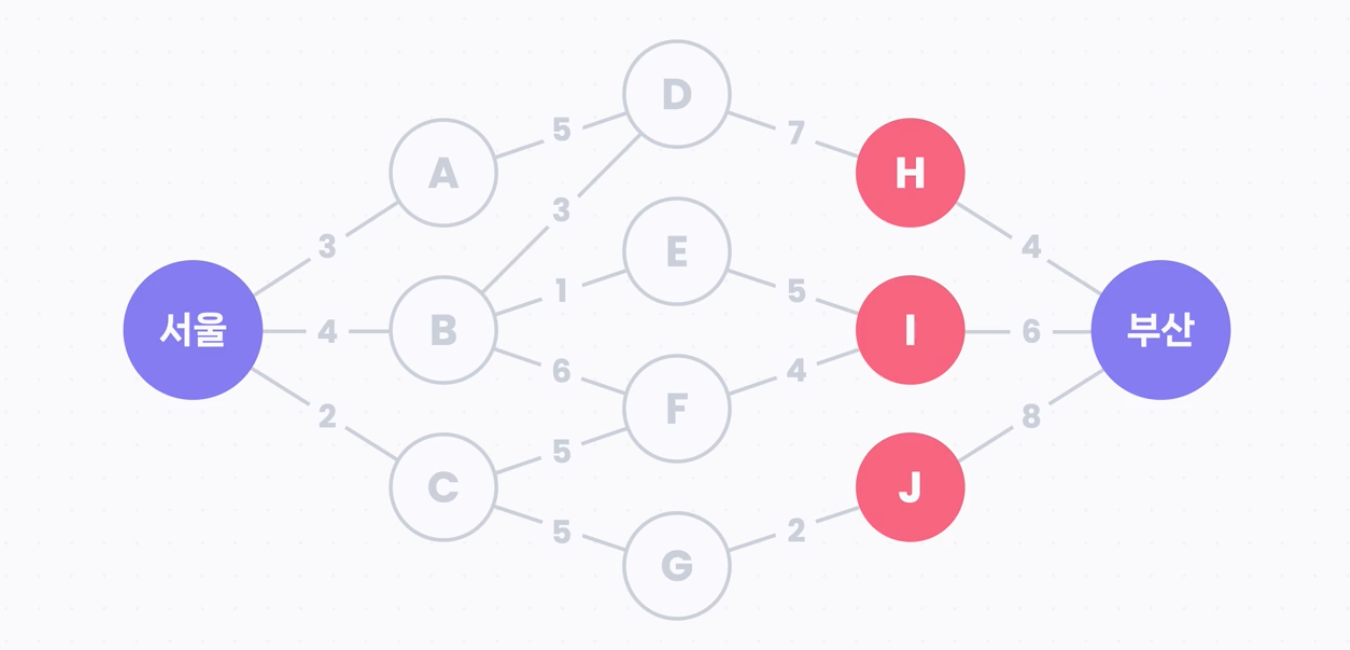
예시2. 최단경로문제
서울에서 부산까지 가는 최단 경로를 찾기 위해 H, I, J에 각각 도착하는 최단 거리(부분문제)를 찾아서 최종적으로 서울에서 부산까지 가는 최단 경로 문제(기존문제)를 풀 수 있다.
🔎 2. 중복되는 부분 구조 (Overlapping Subproblems)
피보나치 함수 fib()를 도식화하면 아래와 같다. fib(5)를 구하기 위해 fib(4), fib(3)이 필요하고, fib(4)를 구하기 위해 fib(3), fib(2)가 필요하다. 쭉 다 써보면 중복되는 문제가 보이는데, 이걸 중복되는 부분구조라고 한다.
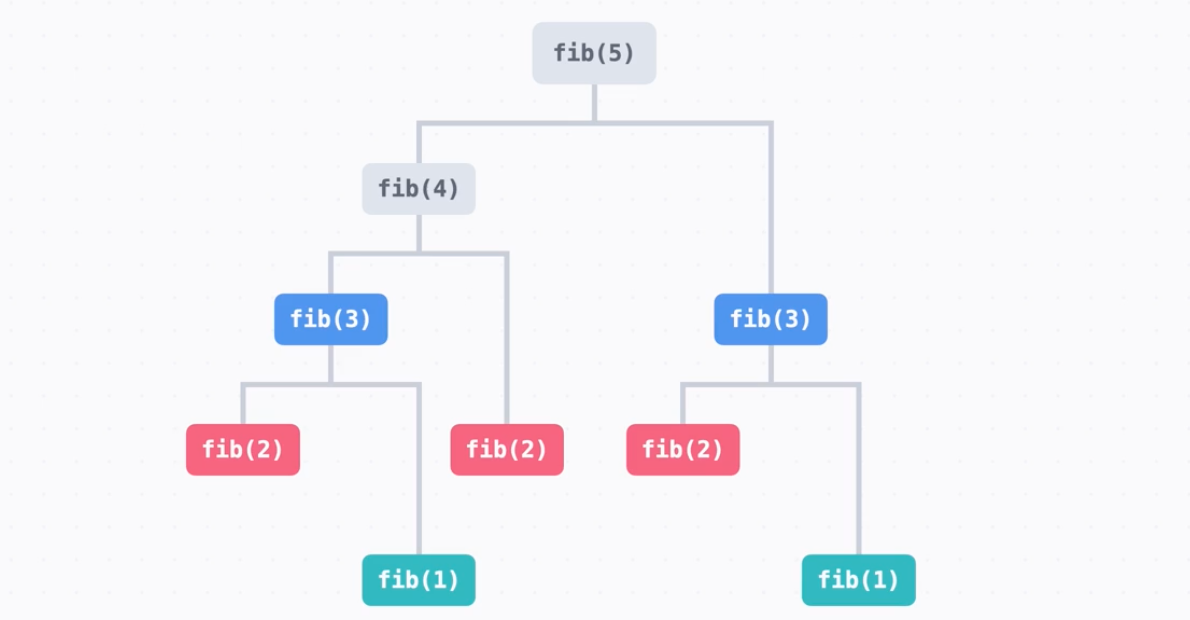
이렇게 중복되는 부분구조를 여러번 계산하는 건 비효율적이기 때문에, 이것을 해결하고자 하는 게 바로 다이나믹 프로그래밍이다.
그런데 문제를 부분문제로 나눈다고 해서 항상 중복되는 부분문제가 있는 것은 아니다. 예를 들어 'Divide&Conquer'를 사용하는 합병정렬(merge sort) 를 보면, 왼쪽과 오른쪽으로 나누는데 이 두 문제는 완전히 독립적이라고 할 수 있다. 따라서 합병정렬의 왼쪽, 오른쪽의 문제는 중복되지 않는 부분문제(Non-overlapping Subproblem) 라고 한다.
어떤 문제에 최적 부분구조가 있다는 건, 부분문제들의 최적의 답을 이용해서 기존문제를 풀 수 있다는 것이다. 따라서 기존문제를 부분문제로 나눠서 풀 수 있는데, 이때 중복되는 부분문제들이 있을 수 있다. 이 중복됨에 따른 비효율을 해결하는 것이 'Dynamic Programming'이다.
따라서, 1) 최적부분구조가 있고, 2) 중복되는 부분문제들이 있으면 다이나믹 프로그래밍을 사용해 해결할 수 있다.
1️⃣ 다이나믹 프로그래밍을 구현하는 두 가지 방식
다이나믹 프로그래밍의 핵심은 '한 번 계산한 결과를 버리지 않고, 재활용하는 방식'이다.
다이나믹 프로그래밍을 구현하는 과정은 아래 두 가지로 나뉜다.
1. Memoization
2. Tabulation🔎 1. Memoization(Top-Down)
중복되는 계산은 한 번만 계산 후 메모하고, 그 이후에는 메모를 참고하는 것
-
하향식 접근 (Top-down Approach)
- fib(5)를 알기 위해 fib(4), fib(3)을 알고, fib(4)를 알기 위해 fib(3), fib(2)를 아는.. 아래로 내려가면서 정답을 알아내는 것
-
재귀적 방법
- fib_memo를 재귀적으로 호출
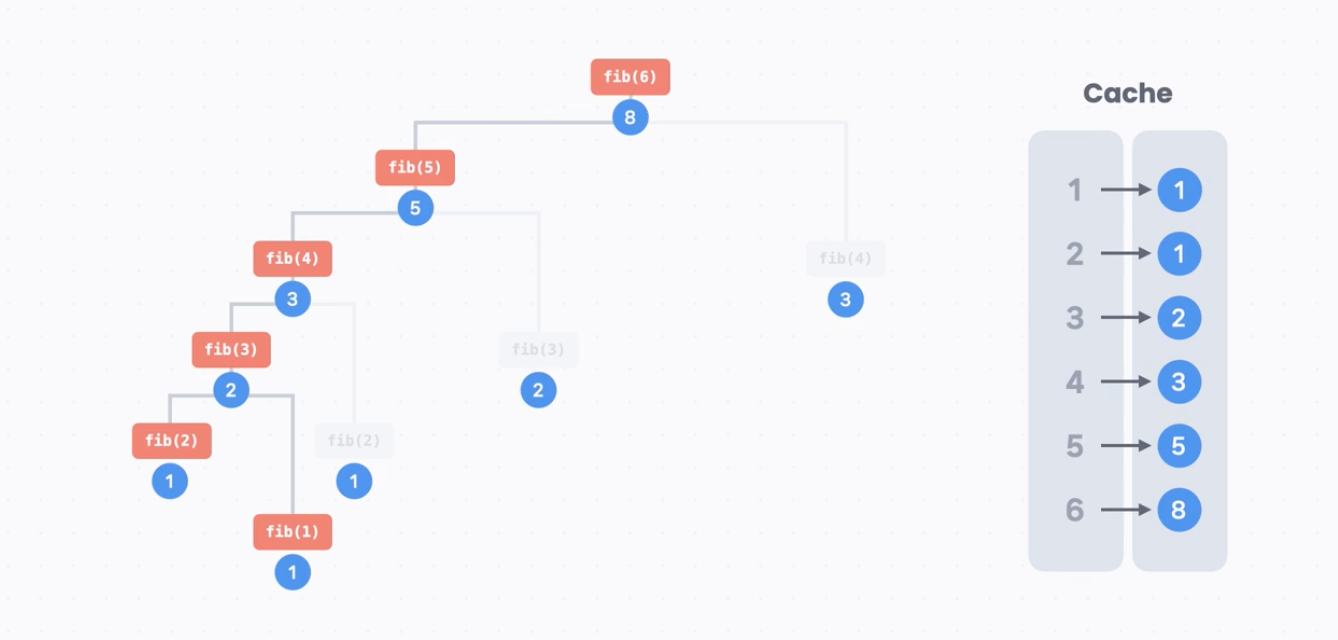
예시) 피보나치 수
다시 쓸 값을 저장하는 곳을 Cache라고 한다. Cache에 다시 쓸 값을 저장해서 필요할 때마다 가져와서 는 방식으로 피보나치 수를 계산할 수 있다.
def fib_memo(n, cache):
if n < 3: # Base Case
return 1
if n in cache: # 이미 n번째 피보나치 계산했으면
return cache[n] # 저장된 값 리턴
else: # 아직 n번째 피보나치 수를 계산하지 않았으면
# 계산을 한 후 cache에 저장
cache[n] = fib_memo(n-1, cache) + fib_memo(n-2, cache)
return cache[n]
def fib(n):
# n번째 피보나치 수를 담는 사전
fib_cache = {}
return fib_memo(n, fib_cache)
# 테스트 코드
print(fib(10))
print(fib(50))
print(fib(100))🔎 2. Tabulation(Bottom-up)
중복되는 것부터 '먼저' 푸는 것으로, 상향식 접근 방식이다.
-
상향식 접근 (Bottom-up Approach)
- fib(5)를 구하기 위해 fib(1), fib(2), fib(3), fib(4)를 구하는 방식으로 아래에서 위로 구하는 걸 상향식 접근이라고 함
Tabulation: 이렇게 테이블을 하나씩 채우는 'Table'방식으로 정리한다는 의미
-
재귀적인 방식인 Memoization과 달리 Tabulation은 반복문의 형태이다. Tabulation 방법으로 피보나치 수열을 구현하면 아래와 같다.
def fib_tab(n): fib_list = [1, 1] for i in range(2, n): fib_list.append(fib_list[i-2]+fib_list[i-1]) return fib_list[-1] # 테스트 코드 print(fib_tab(10)) print(fib_tab(56)) print(fib_tab(132))# 이렇게 해도 됩니당 def fib_tab(n): fib_table = [0] for i in range(1, n): if i <= 2: fib_table.append(i) else: fib_table.append(fib_table[i-1]+fib_table[i-2]) return fib_table[-1] # 테스트 코드 print(fib_tab(10)) print(fib_tab(56)) print(fib_tab(132))
🔎 Memoization vs Tabulation
- 공통점 : 둘 다 중복되는 부분문제의 비효율을 해결한다는 것!
- 차이점
- Memoization은 재귀 사용 -> 재귀적으로 함수를 계속 호출하면 Call Stack이 쌓여 과부화
- Tabulation은 반복문 사용 -> 상향식 방법으로 중간에 필요없는 값도 계산하게 될 수 있음
🔎 Dynamic Programming 공간 최적화
피보나치 문제를 Tabulation으로 풀면 시간복잡도와 공간복잡도 모두 O(n)이다. 위에서 리스트로 하나씩 append하는 방법말고, 공간을 최적화하는 방법을 알아보자.
Tabulation은 리스트를 사용하기 때문에 공간적으로 많이 차지한다.
을 구하기 위해 와 만 알면 된다. 변수 두 개만 쓰면 된다는 얘기다.
current 라는 변수와 previous 변수로만 사용할 수 있다.
previous = 0, current = 1 일 때, 다음 번의 피보나치 수열을 알고 싶다면
- current = current + previous 로 업데이트
- previous = current 로 업데이트
이렇게 풀면 공간을 적게 사용할 수 있다. 사용하는 메모리가 고정되어 있기 때문에 공간 복잡도는 O(1)이다. (시간복잡도는 여전히 O(1)이다..)
DP 문제에서 모든 값을 저장할 필요가 없다면 이렇게 변수를 업데이트하는 방법을 사용해도 좋다.
def fib_optimized(n):
previous = 0
current = 1
for i in range(1, n):
temp = current
current = current + previous
previous = temp
# previous, current = current, previous + current 로도 쓸 수 있다
return current
# 테스트 코드
print(fib_optimized(1)) # 1을 출력
print(fib_optimized(2)) # 1을 출력
print(fib_optimized(3)) # 2을 출력
print(fib_optimized(4)) # 3을 출력
print(fib_optimized(5)) # 5을 출력temp라는 임시변수를 사용하지 않고, swap으로 n_1, n_2 = n_2, n_1 + n_2로도 풀 수 있다. 링크
이렇게 하면 사용하는 메모리는 고정되어 있기 때문에 공간복잡도는 O(1)이다.
Dynaminc Programming을 할 때, 모든 값을 저장할 필요가 없다면 이렇게 공간 사용을 최적화하면 좋다.
코드잇) 새꼼달꼼 장사 Memoization
문제
솔희는 학원 쉬는 시간에 친구들을 상대로 새꼼달꼼 장사를 합니다. 그러다 문뜩, 갖고 있는 새꼼달꼼으로 벌어들일 수 있는 최대 수익이 궁금해졌는데요...
가능한 최대 수익을 리턴시켜 주는 함수max_profit을 작성해 보세요. max_profit은 파라미터로 개수별 가격이 정리되어 있는 리스트price_list와 판매할 새꼼달꼼 개수count를 받습니다.
예를 들어 price_list가 [100, 400, 800, 900, 1000]이라면,
새꼼달꼼 1개에 100원
새꼼달꼼 2개에 400원
새꼼달꼼 3개에 800원
새꼼달꼼 4개에 900원
새꼼달꼼 5개에 1000원
이렇게 가격이 책정된 건데요. 만약 오늘 솔희가 새꼼달꼼 5개를 판매한다면 최대로 얼마를 벌 수 있을까요?
한 친구에게 3개 팔고 다른 친구에게 2개를 팔면,
800 + 400
을 해서 총 1200원의 수익을 낼 수 있겠죠.
풀이
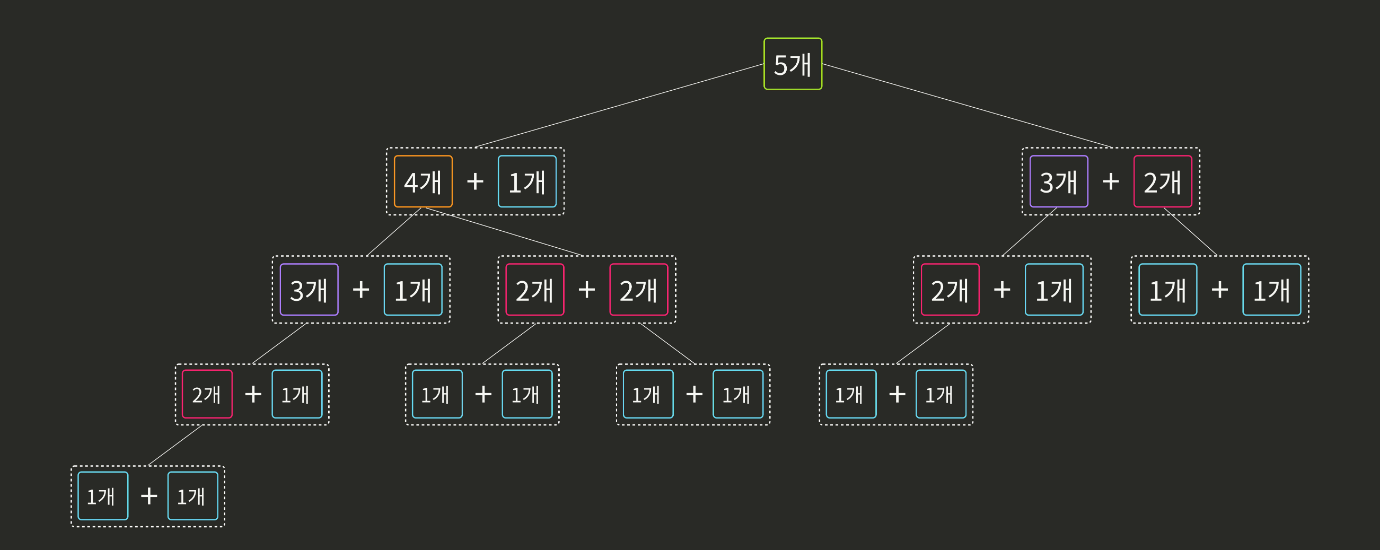
아래처럼 5개를 팔았을 때 최대 이익은
(1) 4개 팔았을 때 최대이익 + 1개 팔았을 때 최대이익
(2) 3개 팔았을 때 최대이익 + 2개 팔았을 때 최대이익
두 가지 경우 중에서의 최대값이다.
- 따라서 Dynamic programming으로 풀 수 있다.
코드
def max_profit_memo(price_list, count, cache):
if count <= 1:
cache[count] = price_list[count]
return cache[count]
if count in cache:
return cache[count]
if count < len(price_list):
profit = price_list[count]
else:
profit = 0
for i in range(1, count//2+1):
profit = max(profit, max_profit_memo(price_list, i, cache)
+ max_profit_memo(price_list, count-i, cache))
cache[count] = profit
return cache[count]
def max_profit(price_list, count):
max_profit_cache = {}
return max_profit_memo(price_list, count, max_profit_cache)
# 테스트 코드
print(max_profit([0, 100, 400, 800, 900, 1000], 5)) # 1200
print(max_profit([0, 100, 400, 800, 900, 1000], 10)) # 2500
print(max_profit([0, 100, 400, 800, 900, 1000, 1400, 1600, 2100, 2200], 9)) # 2400코드잇) 새꼼달꼼 장사 Tabulation
이번엔 위 문제를 반복문을 통해 Tabulation으로 풀어보자
코드
def max_profit(price_list, count):
profit_list = [0]
for i in range(1, count+1):
if i < len(price_list):
profit = price_list[i]
profit_max = [profit_list[x]+profit_list[i-x] for x in range(1, i//2+1)]
profit_max.append(profit)
profit = max(profit_max)
profit_list.append(profit)
return profit_list[count]
# 테스트 코드
print(max_profit([0, 200, 600, 900, 1200, 2000], 5)) # 2000
print(max_profit([0, 300, 600, 700, 1100, 1400], 8)) # 2400
print(max_profit([0, 100, 200, 400, 600, 900, 1200, 1300, 1500, 1800], 9)) #1 800