기계의 문서 유사도 측정 성능에 영향을 미치는 두 요소는 다음과 같다.
- 각 문서의 단어들을 어떤 방법으로 수치화하여 표현했는가
- 문서 간의 단어들의 차이를 어떤 방법으로 계산했는가
✅ 각 문서의 단어들을 어떤 방법으로 수치화하여 표현했는가
텍스트를 컴퓨터가 이해하고 효율적으로 처리하게 하기 위해서는 컴퓨터가 이해할 수 있도록 텍스트를 적절히 숫자로 변환해야 한다. 단어를 표현하는 방법에 따라 자연어 처리 성능은 크게 달라진다. 현재는 각 단어를 인공 신경망 학습을 통해 벡터화하는 워드 임베딩이 가장 많이 사용되고 있다.
📌 임베딩(Embedding)
- 인코딩 : 어떤 단어 혹은 대상을 [0,1,0,0,...] 등 0 또는 1의 숫자로 표현하는 개념
- 임베딩 : 인코딩된 벡터를 [0.1,0.2,0.5,...] 등 밀사람이 쓰는 자연어를 기계가 이해할 수 있는 dense한 벡터로 만들어준다. (밀집 표현)
📌 카운트 기반의 단어 표현(Count based word Representation)
텍스트를 카운트 기반의 텍스트로 수치화하면 통계적인 접근 방법을 통해 여러 문서로 이루어진 텍스트 데이터가 있을 때 어떤 단어가 특정 문서 내에서 단어의 중요도, 문서의 핵심어 추출, 검색 엔진 내 검색 결과의 순위 결정, 문서 간 유사도 측정 등의 용도로 사용할 수 있다.
단어의 표현 방법은 크게 두 가지로 나뉜다.
- 국소 표현(Local Representation)/이산 표현(Discrete Representation)
해당 단어 그 자체만 보고 특정 값을 매핑하여 단어 표현 → puppy, cute, lovely라는 각 단어에 1,2,3을 매핑하여 부여- 분산 표현(Distributed Representation)/연속 표현(Continuous Represnetation)
해당 단어를 표현하고자 주변을 참고하여 단어 표현 → puppy 근처에 주로 cute, lovely가 자주 등장하므로 'puppy'라는 단어는 'cute, lovely한 느낌이다'로 단어 정의
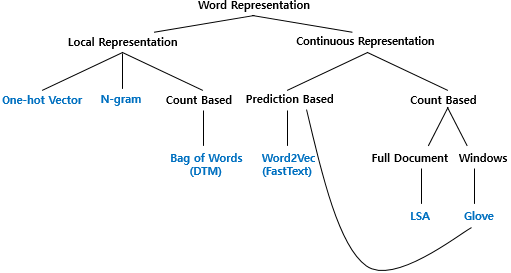
📌 국소 표현 중 카운트 기반 단어 표현 방법
1. Bag of Words(BoW)
Bag of Words는 단어의 순서는 전혀 고려하지 않고 단어들의 출현 빈도에만 집중하는 방법이다. 이름으로 기억하면 쉽다. 어떤 텍스트 문서의 단어들을 가방에 전부 넣고 흔들어 섞었을 때, 문서에 특정 단어가 N번 등장했다면 가방에 특정 단어가 N개 있게 된다. 이 때 단어의 순서는 중요하지 않다.
BoW를 만드는 과정
- 각 단어에 고유한 정수 인덱스 부여(단어 집합 생성)
- 각 인덱스의 위치에 단어 토큰의 등장 횟수를 기록한 벡터 생성(BoW)
CountVectorizer 클래스를 활용한 BoW 예제
사이킷런에서는 단어 빈도를 세서 벡터로 만드는 CountVectorizer 클래스를 지원한다. CountVectorizer는 기본적으로 길이가 2 이상인 문자에 대해서만 토큰으로 인식하며, 띄어쓰기만을 기준으로 단어를 자르는 낮은 수준의 토큰화를 진행하고 있다. 따라서 한국어에는 어려움이 있지만, 영어에 대해서는 이 클래스로 BoW를 쉽게 만들 수 있다.
BoW를 사용한다는 것은 그 문서에서 각 단어가 얼마나 자주 등장했는지 보는 것이기에 자연어 처리 정확도를 높이기 위해 불용어 제거를 하면 좋다. 불용어는 직접 지정하거나 CountVectorizer 또는 NLTK에서 제공하는 불용어를 사용할 수 있다.
2. 문서 단어 행렬(Document-Term Matrix, DTM)
문서 단어 행렬은 서로 다른 문서들의 BoW를 결합한 표현 방법이다. 쉽게 말하면 각 문서에 대한 BoW를 하나의 행렬로 만든 것이며, BoW 표현을 다수의 문서에 대해 행렬로 표현하고 부르는 용어이다. DTM을 통해 서로 다른 문서들을 비교할 수 있고, 행과 열을 반대로 입력하면 TDM이라고 부르기도 한다.
문서 단어 행렬의 표기법
예를 들어 4개의 문서가 있고 띄어쓰기 단어 토큰화를 수행한다고 가정하여 문서 단어 행렬로 표현하면 다음과 같다.
문서1 : 먹고 싶은 사과
문서2 : 먹고 싶은 바나나
문서3 : 길고 노란 바나나 바나나
문서4 : 저는 과일이 좋아요
| 과일이 | 길고 | 노란 | 먹고 | 바나나 | 사과 | 싶은 | 저는 | 좋아요 | |
|---|---|---|---|---|---|---|---|---|---|
| 문서1 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 0 |
| 문서2 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 |
| 문서3 | 0 | 1 | 1 | 0 | 2 | 0 | 0 | 0 | 0 |
| 문서4 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 |
문서 단어 행렬의 한계
-
희소 표현(Sparse representation)
원-핫 벡터와 마찬가지로 대부분의 값이 0으로 표현되는 희소 벡터 또는 희소 행렬이므로 많은 양의 저장 공간과 높은 계산 복잡도를 요구한다. 이는 공간적 낭비와 계산 리소스를 증가시킬 수 있다.BoW 표현을 사용하는 모델에서는 전처리(구두점, 빈도수 낮은 단어, 불용어 제거 및 어간, 표제어 추출을 통한 단어 정규화)를 통해 단어 집합의 크기를 줄이는 일이 중요하다.
-
단순 빈도 수 기반 접근
각 문서에는 중요한 단어와 불필요한 단어들이 혼재되어 있다. 예를 들어, the의 빈도수는 높을 수밖에 없는데 문서 유사도 비교 시 모든 문서에서 the의 빈도수가 높다고 유사한 문서라고 판단해서는 안된다.DTM에 불용어와 중요한 단어에 대해 가중치를 주는 방법을 적용한 TF-IDF가 있다.
3. TF-IDF(Term Frequency-Inverse Document Frequency)
TF-IDF는 단어의 빈도와 역 문서 빈도를 사용하여 DTM을 만든 후 각 단어들마다 중요한 정도를 가중치로 부여하는 방법이다. TF-IDF를 사용하면 기존의 DTM을 사용하는 것보다 많은 정보를 고려하여 문서들을 비교할 수 있다. 항상은 아니지만 대개 DTM보다 더 좋은 성능을 얻을 수 있다.
TF-IDF는 주로 문서 유사도를 구하는 작업, 검색 시스템에서 검색 결과의 중요도를 정하는 작업, 문서 내 특정 단어의 중요도를 구하는 작업 등에 쓰일 수 있다.
TF-IDF는 TF x IDF를 의미한다. 문서를 d, 단어를 t, 문서의 총 개수를 n이라고 할 때 TF, DF, IDF는 다음과 같이 정의할 수 있다.
tf(d,t) : 특정 문서 d에서의 특정 단어 t의 등장 횟수
df(t) : 특정 단어 t가 등장한 문서의 수
idf(t) : df(t)에 반비례하는 수
IDF의 식에 대해서는 부연 설명이 필요하다.
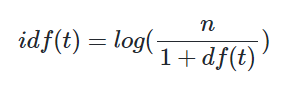
- log를 사용하는 이유
- n이 커질수록 IDF 값이 기하급수적으로 커지는 것을 막기 위해
- 희귀 단어들에 엄청난 가중치가 부여되는 것을 막기 위해
→ TF-IDF는 모든 문서에서 자주 등장하는 단어는 중요도가 낮고, 특정 문서에서만 자주 등장하는 단어의 중요도가 높다고 판단한다. 즉, the나 a 같은 불용어의 경우 다른 단어의 TF-IDF에 비해 낮아지게 된다.
- 분모에 1을 더하는 이유
- 특정 단어가 전체 문서에서 등장하지 않을 경우 분모가 0이 되는 상황을 방지하기 위해
- 극단적으로 큰 IDF 값을 줄여주기 위해
📌 연속 표현
Local Representation은 각 단어를 하나의 개체로 여기고 알고리즘이 교차 단어를 일반화하지 못한다. Continuous Representation은 단어를 고차원 공간에서 연속적인 벡터로 표현하는 방식이다. 대표 예시인 임베딩은 단어, 문장, 문서 등을 실수 벡터로 변환하고 객체 간의 유사성을 숫자 값으로 표현하여 객체를 저차원 공간으로 벡터화한다.
워드 임베딩(Word Embedding)
단어를 밀집 벡터의 형태로 표현하는 방법, 이 밀집 벡터를 워드 임베딩 과정을 통해 나온 결과라고 하여 임베딩 벡터(embedding vector)
희소 표현(Sparse Representation) : 벡터 또는 행렬 값 대부분이 0으로 표현되는 방법
Ex) 강아지 = [ 0 0 0 0 1 0 0 0 0 0 0 0 ... 중략 ... 0] → 이때 1 뒤의 0의 수는 9,995개, 차원은 10,000
- 예시 : 원-핫 벡터, DTM
- 단점 : 공간적 낭비
밀집 표현(Dense Representation) : 사용자가 설정한 값으로 모든 단어의 벡터 표현의 차원을 맞추는 방법
Ex) 강아지 = [0.2 1.8 1.1 -2.1 1.1 2.8 ... 중략 ...] → 이 벡터의 차원은 128
| 원-핫 벡터 | 임베딩 벡터 | |
|---|---|---|
| 차원 | 고차원(단어 집합의 크기) | 저차원 |
| 다른 표현 | 희소 벡터의 일종 | 밀집 벡터의 일종 |
| 표현 방법 | 수동 | 훈련 데이터로부터 학습함 |
| 값의 타입 | 1과 0 | 실수 |
1. 워드투벡터(Word2Vec)
분산 표현(저차원에 단어의 의미를 여러 차원에 분산하여 표현)의 대표적 학습 방법 → 단어 벡터 간 유의미한 유사도 계산 가능
Word2Vec의 학습 방식 1 :CBOW(Continuous Bag of Words)
주변 단어들을 입력으로 중간 단어들을 예측하는 방법
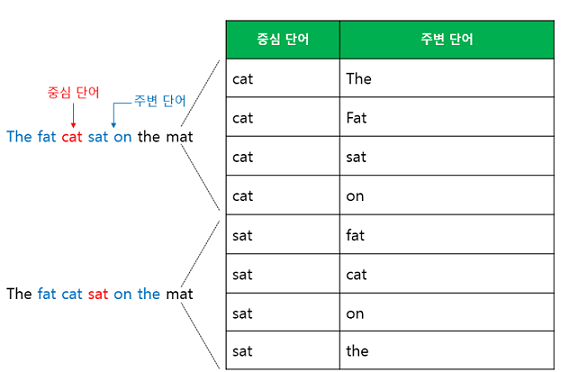
- 윈도우(window) : 중심 단어를 예측하기 위해 앞뒤로 볼 단어 범위(윈도우 크기가 n이라면 중심 단어 예측을 위해 참고하는 주변 단어 수는 총 2n개) → 좌측 이미지
- 슬라이딩 윈도우(sliding window) : 윈도우를 옆으로 움직여서 주변 단어와 중심 단어의 선택을 변경해가며 학습을 위한 데이터셋을 만드는 방법(원-핫 벡터 형태) → 우측 이미지
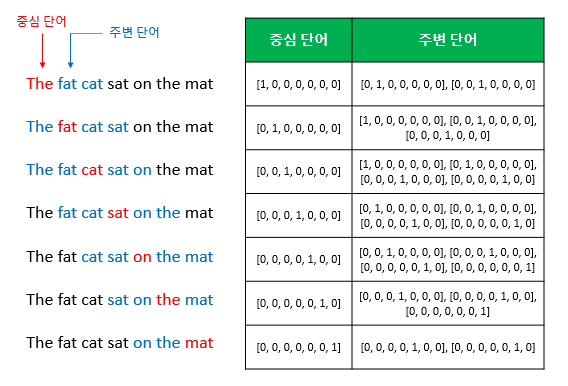
CBOW의 인공 신경망을 보면 Word2Vec은 은닉층이 여러 개인 딥러닝이 아니라 은닉층이 1개인 얕은 신경망이다. 또한 Word2Vec은 일반적인 은닉층과 달리 활성화 함수가 존재하지 않고 룩업 테이블이라는 연산을 담당하는 층으로 투사층(projection layer)를 가진다.
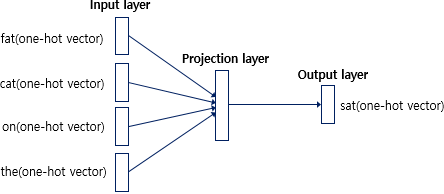
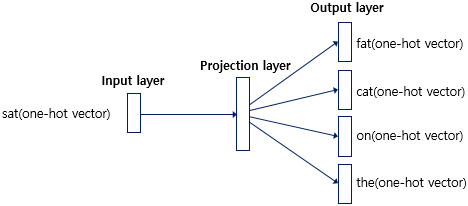
CBOW의 인공 신경망을 확대하여 동작 매커니즘을 살펴보면 다음과 같다.
- CBOW에서 투사층의 크기 M은 임베딩하고 난 벡터의 차원이다. 위 그림에서 CBOW 수행 후 얻는 각 단어의 임베딩 벡터 차원은 5가 될 것이다.
- 입력층과 투사층 사이 가중치 W는 V x M 행렬이며, 투사층과 출력층 사이 가중치 W'는 M x V 행렬이다. V는 단어 집합의 크기를 의미한다. 이때 두 행렬은 동일한 행렬을 전치한 것이 아니라 서로 다른 행렬이다. 인공 신경망 훈련 전 W와 W'는 랜덤 값을 가진다. CBOW는 주변 단어로 중심 단어를 더 정확히 맞히기 위해 W와 W'를 학습해 가는 구조다.
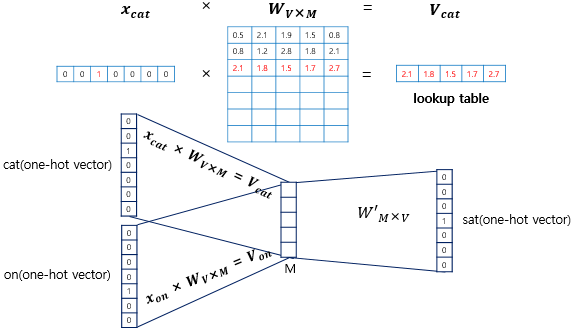
입력 벡터는 각 주변 단어의 원-핫 벡터로, x로 표기하였다. i번째 인덱스에 1을 가지고 그 외 인덱스는 0을 갖는 입력 벡터와 가중치 W 행렬의 곱은 W 행렬의 i번째 행을 그대로 읽어오는 것(lookup)과 동일하다. 이 작업을 룩업 테이블(lookup) 테이블이라고 한다. CBOW의 목적이 W와 W'를 잘 훈련시키는 것이라고 했는데, 그 이유가 여기서 lookup 한 W의 각 행 벡터가 Word2Vec 학습 후에는 각 단어의 M 차원의 임베딩 벡터로 간주되기 때문이다.
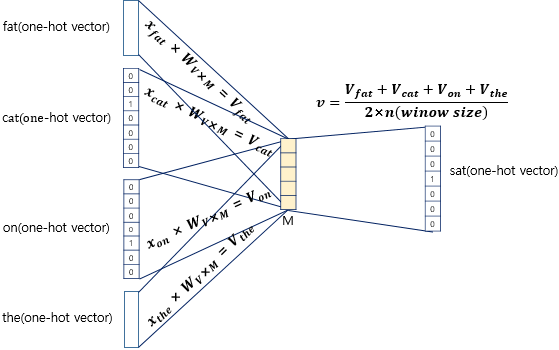
주변 단어의 원-핫 벡터에 대해서 가중치 W가 곱해서 생긴 결과 벡터들은 투사층에서 만나 이 벡터들의 평균인 벡터를 구하게 된다. 윈도우 크기가 2라면 중간 단어 예측을 위해 필요한 입력 벡터는 총 4개이므로 투사층에서 4개의 결과 벡터에 대해 평균을 구하는 것이다. Skip-Gram은 입력이 중심 단어 하나이므로 투사층에서 벡터의 평균을 구하지 않는다는 것이 차이다.
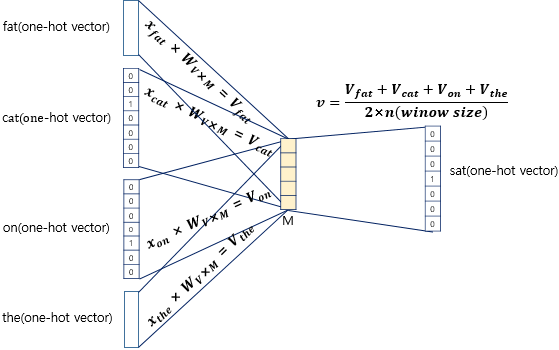
투사층을 지나 구해진 평균 벡터는 두 번째 가중치 행렬 W'와 곱해진다. 곱셈 결과 원-핫 벡터들과 차원이 V로 동일한 벡터가 나온다. 이 벡터에 CBOW는 소프트맥스 함수를 지나며 벡터 각 원소들의 값은 0과 1 사이 실수로, 총 합은 1이 된다. 이는 다중 클래스 분류 문제를 위한 일종의 스코어 벡터로, 스코어 벡터의 j번째 인덱스가 가진 0과 1 사이 값은 j번째 단어가 가진 중심 단어일 확률을 나타낸다. 그리고 이 스코터 벡터 값은 중심 단어의 원-핫 벡터의 값에 가까워져야 하기 때문에 두 벡터 값 오차를 줄이기 위해 CBOW는 손실 함수로 크로스 엔트로피 함수를 사용한다.
크로스 엔트로피 함수에 중심 단어인 원-핫 벡터와 스코어 벡터를 입력 값으로 넣고 식으로 표현하면 아래와 같다. 아래 식에서 V는 단어 집합의 크기다.
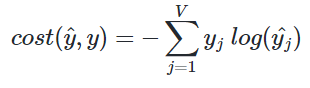
역전파를 수행하면 W와 W'가 학습이 되는데, 학습이 다 되었다면 M 차원의 크기를 갖는 W 행렬의 행을 각 단어의 임베딩 벡터로 사용하거나 W와 W' 행렬 두 가지 모두를 임베딩 벡터로 사용하기도 한다.
Word2Vec의 학습 방식 2 : Skip-gram
중심 단어들을 입력으로 주변 단어들을 예측하는 방법
위와 동일한 예문에 대해 동일하게 윈도우 크기가 2일 때 데이터셋은 우측 이미지와 같다.
인공 신경망을 도식화 하면 아래와 같다. 중심 단어 하나에 대해 주변 단어를 예측하므로 투사층에서 벡터들의 평균을 구하는 과정은 없다. 여러 논문에서 성능 비교를 진행한 결과로는 전반적으로 Skip-gram이 CBOW보다 성능이 좋다고 알려져 있다.
NNLM vs Word2Vec
피드 포워드 신경망 언어 모델(NNLM)은 단어 벡터 간 유사도를 구할 수 있도록 워드 임베딩 개념을 도입하였고, 워드 임베딩 자체에 집중하여 NNLM의 느린 학습 속도와 정확도를 개선한 것이 Word2Vec이다.
| NNLM | Word2Vec | |
|---|---|---|
| 예측 대상 | 다음 단어 | 중심 단어 |
| 참고 단어 | 이전 단어들만 | 예측 단어의 전후 모든 단어 |
| 은닉층 | O | X |
Word2Vec은 은닉층 제거 외에도 계층적 소프트맥스(hierarchical softmax)와 네거티브 샘플링(negative sampling) 기법을 활용하여 학습 속도 측면에서 NNLM보다 강점을 갖는다.
입력층에서 투사층, 투사층에서 은닉층, 은닉층에서 출력층으로 향하며 발생하는 NNLM의 연산량은 다음과 같다.
- NNLM의 연산량 : (n x m)+(n x m x h)+(h x V)
추가적인 기법들까지 사용하였을 때 Word2Vec은 출력층에서의 연산에서 V를 log(V)로 바꿀 수 있는데 이에 따라 Word2Vec의 연산량은 아래와 같으며 이는 NNLM보다 훨씬 빠른 학습 속도를 가진다. - Word2Vec의 연산량 : (n x m)+ (m x log(V))
2. 패스트텍스트(FastText)
페이스북에서 개발한 것으로, 매커니즘 자체는 Word2Vec으로 확장한 것이라고 볼 수 있다. Word2Vec은 단어를 쪼개질 수 업는 단위로 생각한 반면 FastText는 하나의 단어 안에도 여러 단어들이 존재하는 것으로 간주한다. 내부 단어, 즉 서브워드(subword)를 고려하여 학습한다.
내부 단어
FastText에서 각 단어는 글자 단위 n-gram의 구성으로 취급한다. 예를 들어 n=3인 경우 apple은 app, ppl, ple로 분리하고 이들을 벡터로 만든다. 여기에 시작과 끝을 의미하는 <와 >를 도입하고, 기존 단어에 <>를 붙여 총 6개 토큰을 벡터화한다.
# n = 3인 경우
<ap, app, ppl, ple, le>, <apple>실제 사용할 때는 n의 최소값과 최대값으로 범위를 설정할 수 있는데, 기본값으로는 각각 3과 6으로 설정되어져 있다. 다시 말해 최소값 = 3, 최대값 = 6인 경우라면, 단어 apple에 대해서 FastText는 아래 내부 단어들을 벡터화한다.
<ap, app, ppl, ppl, le>, <app, appl, pple, ple>, <appl, pple>, ..., <apple>여기에 내부 단어들을 벡터화한다는 의미는 이 단어들에 대해 Word2Vec을 수행한다는 의미다. 위와 같이 내부 단어들의 벡터 값을 얻었다면 단어 apple의 벡터 값은 위 벡터 값들의 총 합으로 구성한다.
apple = <ap + app + ppl + ppl + le> + <app + appl + pple + ple> + <appl + pple> + , ..., +<apple>Word2Vec과 비교했을 때의 강점
-
모르는 단어(Out Of Vocabulary, OOV)에 대한 대응
FastText의 인공 신경망을 학습한 후에는 데이터 셋의 모든 단어의 각 n-gram에 대해서 워드 임베딩이 된다. 이렇게 되면 데이터 셋만 충분한다면 위와 같은 내부 단어를 통해 모르는 단어(Out Of Vocabulary, OOV)에 대해서도 다른 단어와의 유사도를 계산할 수 있다.
FastText에서 birthplace(출생지)란 단어를 학습하지 않은 상태일 때 다른 단어에서 birth와 place라는 내부 단어가 있었다면, FastText는 birthplace의 벡터를 얻을 수 있습다. 이는 모르는 단어에 제대로 대처할 수 없는 Word2Vec, GloVe와는 다른 점이다. -
단어 집합 내 빈도 수가 적었던 단어(Rare Word)에 대한 대응
Word2Vec의 경우에는 참고할 수 있는 경우의 수가 적다보니 등장 빈도 수가 적은 단어(rare word)에 대해서는 임베딩의 정확도가 높지 않다는 단점이 있었다.
하지만 FastText의 경우, 만약 단어가 희귀 단어라도, 그 단어의 n-gram이 다른 단어의 n-gram과 겹치는 경우라면, Word2Vec과 비교하여 비교적 높은 임베딩 벡터값을 얻는다. 이 때문에 FastText는 빈도수 적은 오타와 같은 노이즈가 많은 코퍼스에서 강점을 가진다.
Word2Vec vs Fasttext 실습 예제 코랩 코드
3. 글로브(GloVe)
글로브(Global Vectors for Word Representation, GloVe)는 카운트 기반과 예측 기반을 모두 사용하는 방법론으로 2014년에 미국 스탠포드대학에서 개발한 단어 임베딩 방법론이다. 기존 카운트 기반의 LSA(Latent Semantic Analysis)와 예측 기반 Word2Vec의 단점을 지적하며 이를 보완한다는 목적으로 나왔고, 실제로도 Word2Vec만큼 뛰어난 성능을 보인다.
윈도우 기반 동시 등장 행렬(Window based Co-occurrence Matrix)
단어의 동시 등장 행렬은 행과 열을 전체 단어 집합의 단어들로 구성하고, i 단어의 윈도우 크기(Window Size) 내에서 k 단어가 등장한 횟수를 i행 k열에 기재한 행렬을 말한다. 아래와 같은 3개 문서로 구성된 텍스트 데이터가 있을 때,
- I like deep learning
- I like NLP
- I enjoy flying
윈도우 크기가 1이라고 하면 좌우 1개의 단어만 참고하여 아래와 같이 동시 등장 행렬이 구성된다.
| 카운트 | I | like | enjoy | deep | learning | NLP | flying |
|---|---|---|---|---|---|---|---|
| I | 0 | 2 | 1 | 0 | 0 | 0 | 0 |
| like | 2 | 0 | 0 | 1 | 0 | 1 | 0 |
| enjoy | 1 | 0 | 0 | 0 | 0 | 0 | 1 |
| deep | 0 | 1 | 0 | 0 | 1 | 0 | 0 |
| learning | 0 | 0 | 0 | 1 | 0 | 0 | 0 |
| NLP | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| flying | 0 | 0 | 1 | 0 | 0 | 0 | 0 |
위 행렬은 행렬을 전치(Transpose)해도 동일한 행렬이 된다는 특징이 있다.
동시 등장 확률(Co-occurrence Probability)
동시 등장 확률 P(k|i)는 동시 등장 행렬로부터 특정 단어 i의 전체 등장 횟수를 카운트하고, 특정 단어 i가 등장했을 때 어떤 단어 k가 등장한 횟수를 카운트하여 계산한 조건부 확률이다. i를 중심 단어(Center Word), k를 주변 단어(Context Word)라고 했을 때, 위에서 배운 동시 등장 행렬에서 중심 단어 i의 행의 모든 값을 더한 값을 분모로 하고 i행 k열의 값을 분자로 한 값이라고 볼 수 있다.
| 동시 등장 확률과 크기 관계 비(ratio) | k=solid | k=gas | k=water | k=fashion |
|---|---|---|---|---|
| **P(k | ice)** | 0.00019 | 0.000066 | 0.003 |
| **P(k | steam)** | 0.000022 | 0.00078 | 0.0022 |
| **P(k | ice) / P(k | steam)** | 8.9 | 0.085 |
손실 함수(Loss function)
GloVe의 목표는 '임베딩 된 중심 단어와 주변 단어 벡터의 내적이 전체 코퍼스에서의 동시 등장 확률이 되도록 만드는 것'이다. 이를 위해 동시 등장 확률을 기반으로 임베딩 벡터를 학습한다. GloVe는 중심 단어와 주변 단어 벡터의 내적이 동시 등장 확률을 잘 표현하도록 임베딩 벡터를 설계한다. 손실 함수는 실제 동시 등장 확률과 임베딩 벡터를 통해 계산된 확률 사이의 차이를 최소화하도록 설정된다. 이 과정을 통해 단어 간의 의미적 유사성을 잘 반영하는 벡터를 학습하게 된다.
✅ 문서 간의 단어들의 차이를 어떤 방법으로 계산했는가(벡터의 유사도)
단어를 수치화했다면 여러 유사도 기법을 활용하여 문서의 유사도를 구할 수 있다.
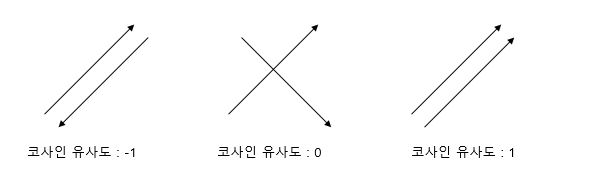
📌 코사인 유사도
두 벡터 간의 코사인 각도를 이용하여 구할 수 있는 두 벡터의 유사도
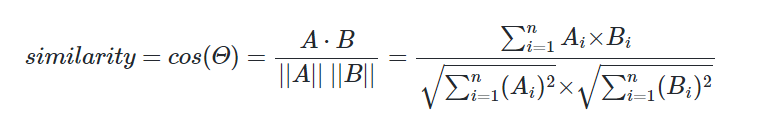
예시 문서
- 문서1 : 저는 사과 좋아요
- 문서2 : 저는 바나나 좋아요
- 문서3 : 저는 바나나 좋아요 저는 바나나 좋아요
띄어쓰기 기준 토큰화를 진행했을 때 문서 단어 행렬은 다음과 같다.
| 바나나 | 사과 | 저는 | 좋아요 | |
|---|---|---|---|---|
| 문서1 | 0 | 1 | 1 | 1 |
| 문서2 | 1 | 0 | 1 | 1 |
| 문서3 | 2 | 0 | 2 | 2 |
유사도 계산
import numpy as np
from numpy import dot
from numpy.linalg import norm
def cos_sim(A, B):
return dot(A, B)/(norm(A)*norm(B))
doc1 = np.array([0,1,1,1])
doc2 = np.array([1,0,1,1])
doc3 = np.array([2,0,2,2])
print('문서 1과 문서2의 유사도 :',cos_sim(doc1, doc2))
print('문서 1과 문서3의 유사도 :',cos_sim(doc1, doc3))
print('문서 2와 문서3의 유사도 :',cos_sim(doc2, doc3))
----------
문서 1과 문서2의 유사도 : 0.67
문서 1과 문서3의 유사도 : 0.67
문서 2과 문서3의 유사도 : 1.00문서3은 문서2에서 모든 단어의 빈도 수가 1씩 증가하기만 했다. 문서1과 문서2는 길이가 비슷하다. 이 경우 유클리드 거리로 유사도를 연산하면 문서1이 문서2보다 문서3과 유사도가 더 높게 나올 수 있는데, 코사인 유사도를 벡터의 방향(패턴)에 초점을 두기 때문에 문서 길이가 다른 상황에서 비교적 공정한 비교를 할 수 있도록 도와준다.
📌 유사도 기법들
- 유클리드 거리(Euclidean distance)
2차원 좌표 평면 상에서 두 점 p와 q 사이의 직선 거리를 구하는 문제

import numpy as np
def dist(x,y):
return np.sqrt(np.sum((x-y)**2))
doc1 = np.array((2,3,0,1))
doc2 = np.array((1,2,3,1))
doc3 = np.array((2,1,2,2))
docQ = np.array((1,1,0,1))
print('문서1과 문서Q의 거리 :',dist(doc1,docQ))
print('문서2과 문서Q의 거리 :',dist(doc2,docQ))
print('문서3과 문서Q의 거리 :',dist(doc3,docQ))- 자카드 유사도(Jaccard similarity)
합집합에서 교집합의 비율을 구한다면 두 집합 A와 B의 유사도를 구할 수 있다는 아이디어
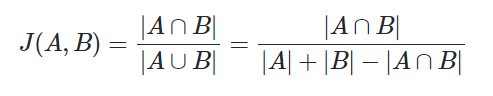
doc1 = "apple banana everyone like likey watch card holder"
doc2 = "apple banana coupon passport love you"
# 토큰화
tokenized_doc1 = doc1.split()
tokenized_doc2 = doc2.split()
union = set(tokenized_doc1).union(set(tokenized_doc2))
intersection = set(tokenized_doc1).intersection(set(tokenized_doc2))
print('자카드 유사도 :',len(intersection)/len(union))