<그래프의 기본>
그래프 = node + edge
-
node: 데이터를 표현하는 단위
-
edge: 노드를 연결해줌
그래프 알고리즘
1. 유니온 파인드
그래프의 사이클이 생성되는지를 판별하는 알고리즘
2. 위상 정렬
- 조건
i) 사이클 X (전-후 관계가 있음) ii) 방향 O
-
특징 : 값(결과)이 유일하지 않음
-
예시: 수강신청 (과목 I -> 과목 II)
3. 최단거리 알고리즘
3-1. 다익스트라
- 조건 : 음수 간선 X
- 특징 : 시작점이 있고, 다른 모든 노드로 가는 최단거리를 구하는 알고리즘
3-2. 벨만-포드
-
조건 : 음수 간선 O
-
특징 : 시작점이 있고, 다른 모든 노드로 가는 최단거리를 구하는 알고리즘
-> 음수 사이클이 있는지 체크하는 문제 많이 나옴 -
예시 : 시간여행 할 수 있는지? (과거로 돌아갈 수 있는지)
3-3. 플로이드-워셜
- 특징 : 시간 복잡도가 안 좋음 → n이 작은 문제일 때 사용하기 좋음
시작점이 주어지지 않음, 모든 노드의 최단거리를 구할 수 있음
4. 최소 신장 트리
- 정의 : 그래프에서 최소의 가중치 합으로 모든 노드를 연결할 수 있게 해주는 알고리즘
- 특징 : 간선의 가중치가 최소가 되게끔 구하는 알고리즘,
유니온 파인드가 필요함 (사이클이 나올 수 없기에)
<그래프의 표현>
- 그래프를 표현하는 3가지 방법
1) 에지 리스트 , 2) 인접 행렬, 3) 인접 리스트
에지 리스트
-> 에지 중심으로 그래프 표현
가중치 없는 그래프 표현
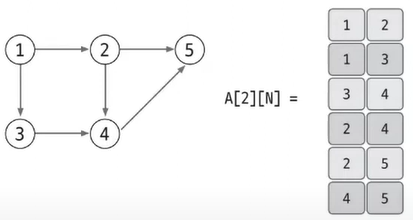
가중치가 있는 표현
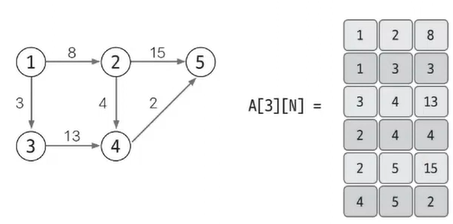
- 특정 노드와 관련되어 있는 에지를 탐색하기는 쉽지가 않음
인접 행렬
-> 2차원 배열을 자료구조로 이용하여 그래프로 표현
(노드 중심으로 그래프 표현)
인접 행렬을 이용하여 가중치가 없는 그래프 표현
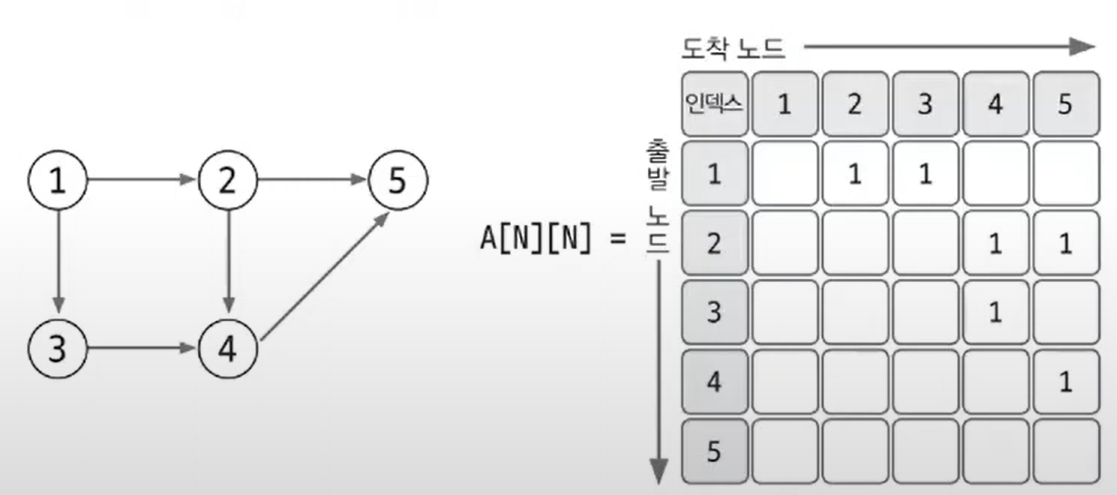
인접 행렬을 이용한 가중치가 있는 그래프 표현

- 노드와 관련되어 있는 에지를 탐색하려면 N번 접근해야 하므로 노드 개수를 비해 에지가 적을 때는 공간 효율성을 떨어짐 -> 노드 개수에 따라 사용 여부를 적절하게 판단하는 능력이 필요함
인접 리스트
가장 많이 사용함.
그래프 구현은 복잡하지만, 노드와 연결되어 있는 에지를 탐색하는 시간이 매우 뛰어나고 메모리 초과 에러도 발생하지 않음.
인접 리스트로 가중치 없는 그래프 표현하기
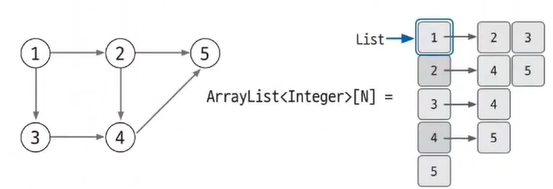
ArrayList<Integer>[N]인접 리스트로 가중치 없는 그래프 표현
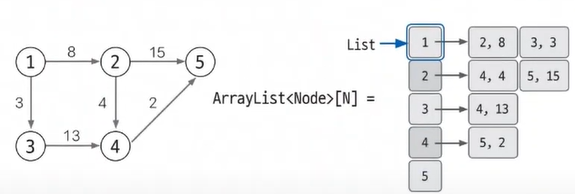
ArrayList<Node>[N]Node -> class