[Algorithm]Brute-force Algorithm

정의

• 가능한 모든 경우의 수를 무식하게 (=brute-force) 전부 탐색해서 정답을 찾는 방법
• 일종의 완전 탐색 기법으로, 문제 해결을 위해 조건을 만족하는 모든 조합이나 경우를 일일이 검사함

특징

• 직관성
  구현이 매우 단순하고 직관적임

• 정확도
  정답을 반드시 찾을 수 있음(단, 경우의 수가 많으면 매우 비효율적임)

• 성능
  일반적으로 시간 복잡도가 매우 높음 (보통 O(n^2, O(n!))

• 사용 조건
  입력 크기가 작거나 가능한 경우의 수가 제한적일 때 적합

종류

1. 선형 구조 -> 순차탐색
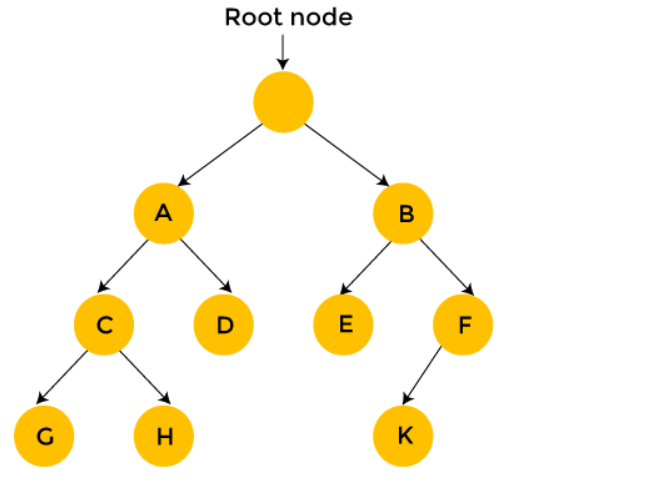
2. 비선형 구조 -> BFS, DFS

<순차탐색>

1) 문제에서 주어진 자료 -> 선형구조로 바꿈
2) 구조화된 자료들은 구조에 맞는 방법으로 해를 구할 때까지 탐색
3) 탐색한 해를 주어진 문제 형식에 맞게 정리

예시

1. 반복문을 사용하는 경우

대부분은 반복문과 조건문을 활용해서 모든 경우를 탐색함

<숫자형 자물쇠>
비밀번호를 잊어버렸다면, 000 부터 999까지 하나씩 돌리는 방식으로 비밀번호를 구할 수 있고, 자물쇠가 풀렸다면, 더는 돌릴 필요가 없음

public class example {

    static int [] password = {3,4,5};

    public static void main(String[] args) {

        for(int i = 0 ; i < 10 ; i ++){
            for(int j = 0 ; j < 10 ; j ++){
                for(int k = 0 ; k < 10 ; k ++){

                    if(password[0] == i && password[1] == j && password[2] == k){

                        System.out.println("자물쇠 해제 ");
                        System.out.println("비밀번호는 " + i + j + k);
                        break;
                    }

                }
            }
        }
    }
}

2. 재귀를 사용하는 경우

<10 팩토리얼을 구하는 문제>

public class example {

    public static void main(String[] args) {
        System.out.println( "10 factorial = " + factorial(10));

    }

    public static int factorial(int n) {
        if (n == 1) {
            return 1;
        } else {
            return n * factorial(n - 1);
        }
    }
}