99클럽 코테 스터디
3월 25일부터 5주간 진행되는 스터디에 중도 참여하였는데, 그래서 그런지 첫날부터 문제가 굉장히 어려웠다.
유니온 파인드 기법으로 풀려다가 1시간여동안 삽질하고 나서 지인의 조언으로 다익스트라로 접근하여 풀 수 있었다.
풀고 나서 스터디원들에게 풀이도 공유하여 설명했는데, 좀 늦게 풀어서 대부분 전체 해설을 들으러 갔고, 남은 6명(나 포함)에게만 설명하였다.
풀이 접근
접근한 방법은, 모든 산봉우리에서 출발하여 한 칸씩 이동하면서 다익스트라 기법을 적용하는 것이다. 원래는 출입구에서 출발하여 산봉우리를 찍고 다시 내려오는 것이지만, 문제의 조건상 산봉우리에서 출발해서 편도로 출입구에 도달하여도 최단거리가 같기 때문이다.
다익스트라를 쓰기 위해 우선순위 큐에 넣을 파라미터로는
- 해당 점에 도달하는 거리 (이 문제는 특이하게, 1->2->3으로 이동하면 1->2의 거리와 2->3의 거리를 합하지 않고 둘 중 최대값으로 결정된다)
- 출발한 산봉우리의 번호 (같은 최단거리로 여러 가지 경로가 있으면 도달한 산봉우리 번호가 낮은 쪽을 택해야 하기 때문)
- 현재 점의 번호
순으로 적용했고, 방문한 점은 1차원 배열을 이용해 visited 처리하여 다음에 다른 경로로 방문했을 때는 넘겨버렸다. (위 3가지 파라미터를 적용한 우선순위 큐에서 나온 순서대로라면 같은 점으로 도달하는 경로 중 먼저 나온 쪽이 우월한 경로라고 판단했기 때문이다.)
출입구도 정해진 게 아니고 여러 개 있기 때문에, 현재 node가 출입구인지 아닌지도 매번 in 함수로 검색하면 시간초과되므로 (n^2, n≤50000) 출입구인지 아닌지도 따로 1차원 배열로 저장해두었다.
틀왜맞?
근데 사소한? 문제가 하나 있었으니...
풀고 나서 같은 스터디원들에게 풀이를 공유하고 설명해 봤는데, 설명하다 보니 그림판에 그려놓은 예시가 반례라는 걸 깨달았다. 근데 내 코드는 이미 정답으로 통과된 뒤였다.
프로그래머스 사이트에 익숙치 않아서 문제 질문 게시판에 올려두었는데, 따로 반례를 제보하는 기능이 있는지는 모르겠다.
반례 및 해설
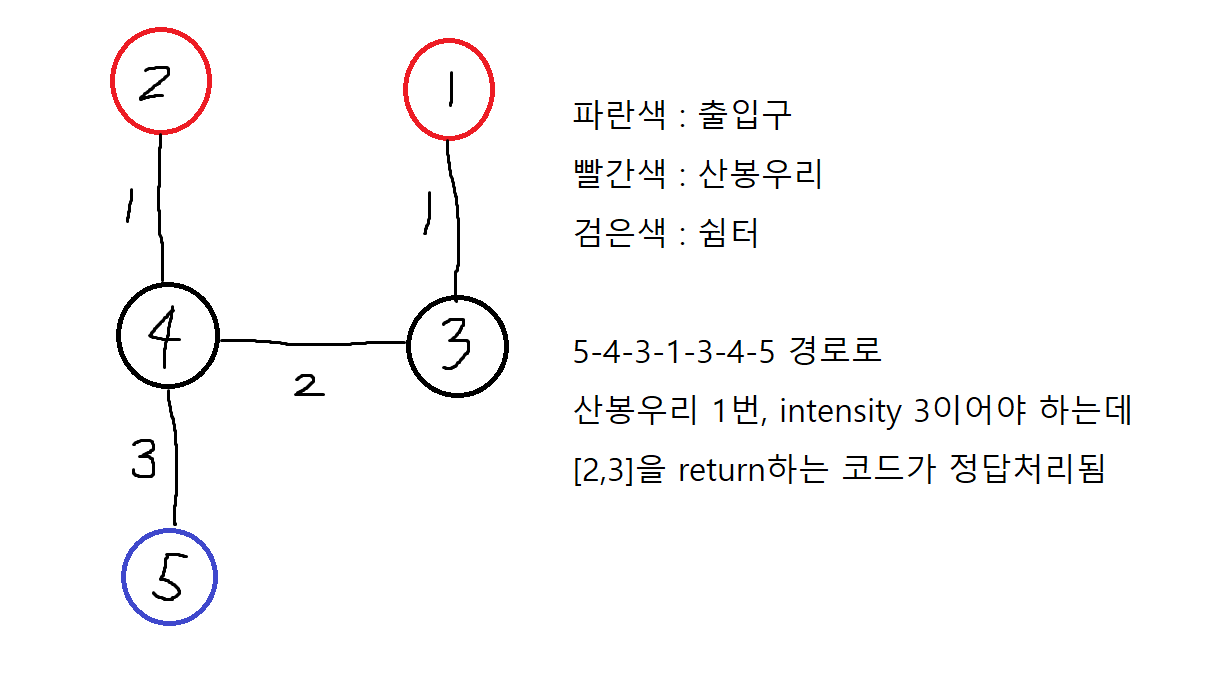
아래 그림에서, 내 풀이대로라면 1->3->4로 가는 경로는 intensity 2, 2->4로 가는 경로는 intensity 1이다. intensity는 이 문제에서 거리를 의미한다.
그리고 우선순위 큐의 첫 번째 파라미터가 intensity이므로 1->3->4 경로보다 2->4 경로가 우월하다고 판단하여 1->3->4 경로는 스킵된다. 그러고 나서 2->4->5 경로로 intensity 3이 최선이라 판단하고 그대로 2,3(산봉우리 2번, intensity 3)을 반환하고 종료된다.
구체적으로는, heap에 [(1,1,3),(1,2,4)]가 들어있는 상태로 시작하여, 가장 먼저 (1,1,3)이 pop되고(intensity 1, 출발한 산봉우리 1번, 현재 위치 3번), 3번 노드와 연결된 1,4번 노드를 heap에 넣고...
해설 쓰다 생각난 피드백
하지만 1번 노드(1번 산봉우리)는 visited 처리되어 있으므로 나중에 힙에서 꺼냈을 때 무효로 처리하여 넘겨버린다. 사실 이럴 거면 힙에 넣기 전에 visited 여부를 확인하고 미방문한 점만 넣는 게 효율적이다. 하지만 visited 처리된 점을 넘겨버리는 방법 자체가 틀린 원인이므로 효율성 증대를 위해 반영할 일은 없겠다.
아무튼 4번 노드만 heap에 넣는다 치고, 4번 노드는 (2,1,4)의 형태로 heap에 들어간다. (intensity 2, 출발한 산봉우리 1번, 현재 위치 4번)
즉 heap은 [(1,2,4),(2,1,4)]가 되고, 여기서 (1,2,4)를 pop한 뒤 (마찬가지 과정으로) (3,2,5)를 heap에 넣고, [(2,1,4), (3,2,5)]에서 (2,1,4)를 pop했는데 4번 노드가 방문처리되어 있으므로 캔슬되고, 마지막 남은 (3,2,5)를 pop하면 5번 노드는 출입구이므로 2번 산봉우리를 찍고 오는 intensity 3의 경로가 최선이다---라고 결론을 내리게 되는 것이다.
여기서 문제는 (2,1,4)(intensity 2, 출발한 산봉우리 1번, 현재 위치 4번, 의미상으론 1->3->4 경로를 의미한다)를 캔슬하지 않아야 한다는 것이고, 이를 위해 예외처리를 포함한 풀이 보강이 필요하다.
틀린 부분 보강(실패)
보강하는 법은 간단할 줄 알았는데, 생각보다 예외 처리가 복잡하다. 대충 처리해 버리면 시간복잡도에 걸려버리거나 다른 반례가 생긴다. (n^2이면 시간초과)
이리 생각하고 저리 생각해 봐도, 출입구에서 출발하는 게 맞는 것 같다. 산봉우리에서 출발하면 풀이를 어떻게 보강해도 시간복잡도 or 반례에 걸리는 것 같다(훌륭한 방법이 있을 수도 있지만 생각해내지 못했다).
보강하는 방법은 두 가지 생각해 봤는데, 두 방법 다 위 그림의 반례는 해결 가능하지만, 방법 자체를 설명하기엔 조금 길고 각각에 대해 새로운 반례가 있다.
- 하나는 위 그림에서 4->5로 가는 길이 3 경로를 없애고, 새로운 6번 쉼터를 만들고, 4->6 길이 1, 5->6 길이 3 경로를 추가하면 새로운 반례가 나온다.
- 하나는 위 그림에서 2번 산봉우리 번호를 6번으로 바꾸고, 새로운 2번 산봉우리를 만들고, 2->5 길이 3 경로를 추가하면 새로운 반례가 나온다.
- 두 경우 다 정답인 [1,3] 대신 여전히 [2,3]을 return한다.
개정된 풀이
즉, 산봉우리에서 출발한다는 아이디어는 접어두고 얌전히 출입구에서 출발하는 게 맞았던 것 같다.
이 방법이 힙에 넣을 것도 (w,s,p) 대신 (w,p)로 간단해지고, p가 출입구인지 확인하는 대신 산봉우리인지 확인해서 while문을 끝내면 intensity가 같을 때 산봉우리 번호를 최소로 하여야 한다는 조건도 보장 가능하다.
근데 왜 산봉우리에서 출발했느냐면, 유니온 파인드 기법으로 접근할 때 생각난 반례를 타파하기 위해 산봉우리에서 출발한다는 아이디어를 생각했는데, 다익스트라로 풀이법을 바꾸고 나서도 산봉우리에서 출발해 버리니까 이런 반례가 나온 것 같다...
기존 코드 (틀왜맞)
원래 풀이 코드와, 프로그래머스에 반례를 직접 테스트케이스로 넣어 실행한 결과를 첨부하였다.
import heapq
def solution(n, paths, gates, summits):
answer = []
heap = []
connected = [[] for i in range(n+1)]
visited = [False] * (n+1)
is_gate = [False]* (n+1)
for g in gates:
is_gate[g] = True
for p in range(len(paths)):
path = paths[p]
i,j,w = path[0],path[1],path[2]
connected[i].append((w,j))
connected[j].append((w,i))
for s in summits:
visited[s] = True
for w,p in connected[s]:
heapq.heappush(heap,(w,s,p))
while heap:
w,s,p = heapq.heappop(heap)
if visited[p]:
continue
if is_gate[p]:
answer = [s,w]
break
visited[p] = True
for new_w, new_p in connected[p]:
heapq.heappush(heap,(max(w,new_w),s,new_p))
return answer테스트 5
입력값 〉 5, [[1, 3, 1], [2, 4, 1], [3, 4, 2], [4, 5, 3]], [5], [1, 2]
기댓값 〉 [1, 3]
실행 결과 〉 실행한 결괏값 [2,3]이 기댓값 [1,3]과 다릅니다


오늘 발표 잘들었습니다!!