99클럽(2기) 코테 스터디 15일차 TIL (Fibonacci Number, Count Square Submatrices with All Ones, 도둑질)
TIL2
99클럽 코테 스터디
오늘도 dp였다. 특이한 점은, 미들러 문제가 챌린저 문제보다 훨씬 어려웠다. 풀이에 접근하기도 꽤 어려웠고, 미들러 문제를 거의 다 풀어 놓고 이상한 데서 실수해서 오래 찾기도 했다. 그래도 다 잘 풀어낸 것 같다.
비기너 문제 Fibonacci Number : https://leetcode.com/problems/pascals-triangle/description/
미들러 문제 Count Square Submatrices with All Ones : https://leetcode.com/problems/count-sorted-vowel-strings/description/
챌린저 문제 도둑질 : https://school.programmers.co.kr/learn/courses/30/lessons/43105
출처 : 프로그래머스, leetcode
비기너 문제 : Fibonacci Number
풀이 접근
아마도? 유명한 문제이다. 그리고 이런 류의 문제 특징은, 꼴랑 30까지는 하드코딩하기가 아주아주 쉬워서 피보나치 수열의 30항까지를 다 써놓고 그걸 return하면 가장 빠른 풀이가 되어버린다.
반대로, 이 문제를 재귀를 배운 직후에 접하고 바로 순진하게 쌩 재귀로 풀면 바로 시간초과가 뜰 것이다. dp를 이용해서 푸는 것이 정석이다.
코드(Python3, Accepted, 27ms(상위 4.6%), 16.36MB(상위 4.26%))
하드코딩 없이 푼 것중엔 아마 최선의 결과일 것이다. 수열의 첫 두개 항을 넣어두고, 피보나치 수열의 점화식대로 n항까지 만들어낸다.
class Solution:
def fib(self, n: int) -> int:
fib_nums = [0,1]
for i in range(n - 1):
fib_nums.append(fib_nums[i] + fib_nums[i+1])
return fib_nums[n]
미들러 문제 : Count Square Submatrices with All Ones
풀이 접근
아이디어를 떠올리는 게 굉장히 어려운 문제이다. 떠올리고 나면 쉽다. (아마도?)
matrix의 각 원소에 대해서, 그 자리를 맨 오른쪽 밑으로 하는 정사각형의 개수를 센다.
이게 아이디어의 핵심이다. 잠깐 생각해보면 알 수 있겠지만, 해당 개수는 같은 조건으로 만들 수 있는 가장 큰 정사각형의 한 변의 길이와 같다. 그리고 따로 이중 리스트(보통 dp라고 이름짓는)를 만들 필요도 없이, matrix를 순차적으로 변형시키면서 찾을 수 있다.
i행 j열의 원소(matrix[i][j])를 맨 오른쪽 밑으로 하는 정사각형의 개수를 찾는 논리는 다음과 같다. (당연하지만, matrix[i][j]가 0이면 살펴볼 필요도 없이 그대로 0이므로, 1일 경우에만 개수를 찾는다)
- 그 원소의 바로 왼쪽과 바로 위 원소의 값이 서로 같을 경우
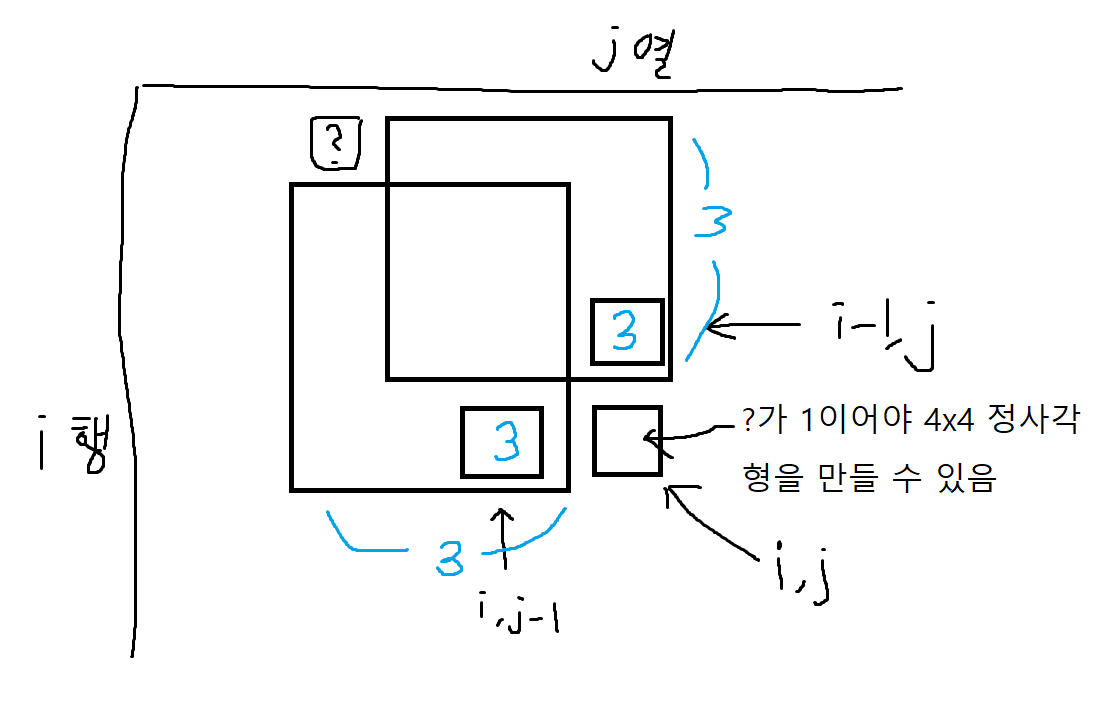
예를 들어, 바로 왼쪽도 3, 바로 위쪽도 3인 경우를 살펴보자. 이는, matrix[i-1][j]를 가장 오른쪽 밑으로 하는 최대의 정사각형의 크기, 그리고 matrix[i-1][j]를 가장 오른쪽 밑으로 하는 최대의 정사각형 크기가 둘 다 3임을 의미한다.
따라서, matrix[i][j]의 값은 3 이상임이 보장되고(위 그림에서 3x3 정사각형 두 개가 차지하는 부분은 모두 1이므로, matrix[i][j]를 포함해서 3x3 정사각형은 확정됨),
반대로 matrix[i][j]의 값이 5 이상일 수는 없다(만약 5라면, 당연하게도 matrix[i-1][j]와 matrix[i][j-1] 둘 다 4 이상이어야 한다).
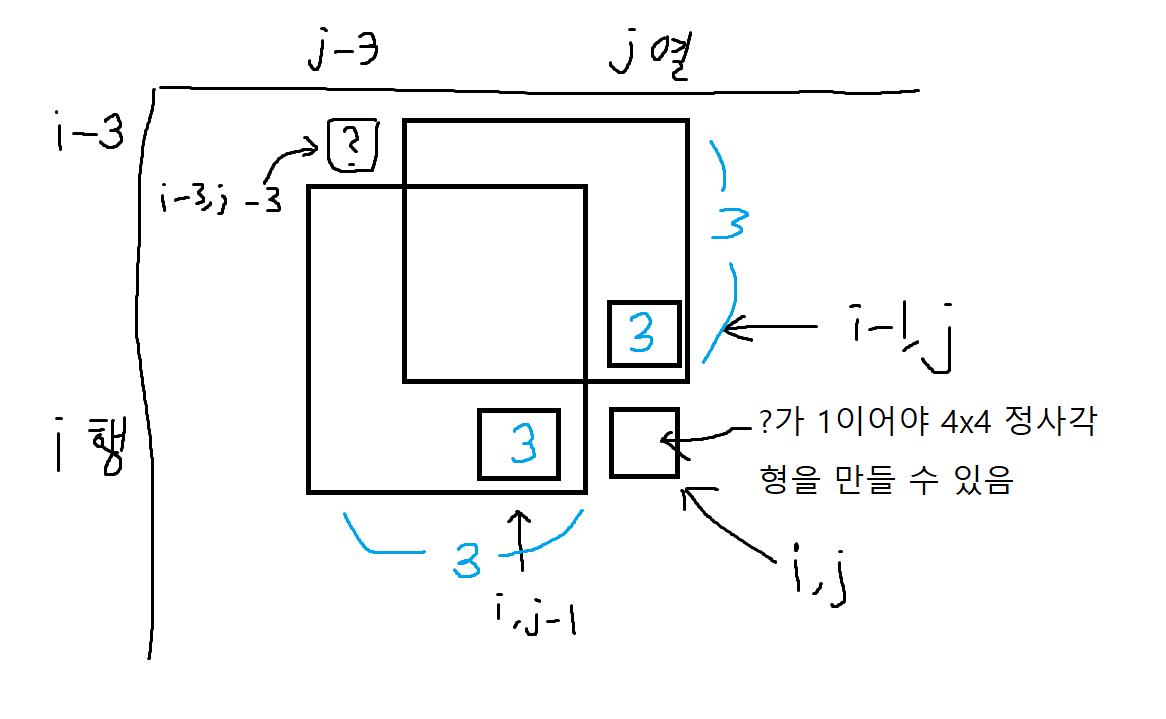
그리고, matrix[i][j]가 3인지 4인지는, matrix[i-3][j-3]이 결정한다.
해당 위치의 값이 1이면 matrix[i][j]는 4가 되고, 0이면 3이 된다.
- 그 원소의 바로 왼쪽과 바로 위 원소의 값이 서로 다를 경우
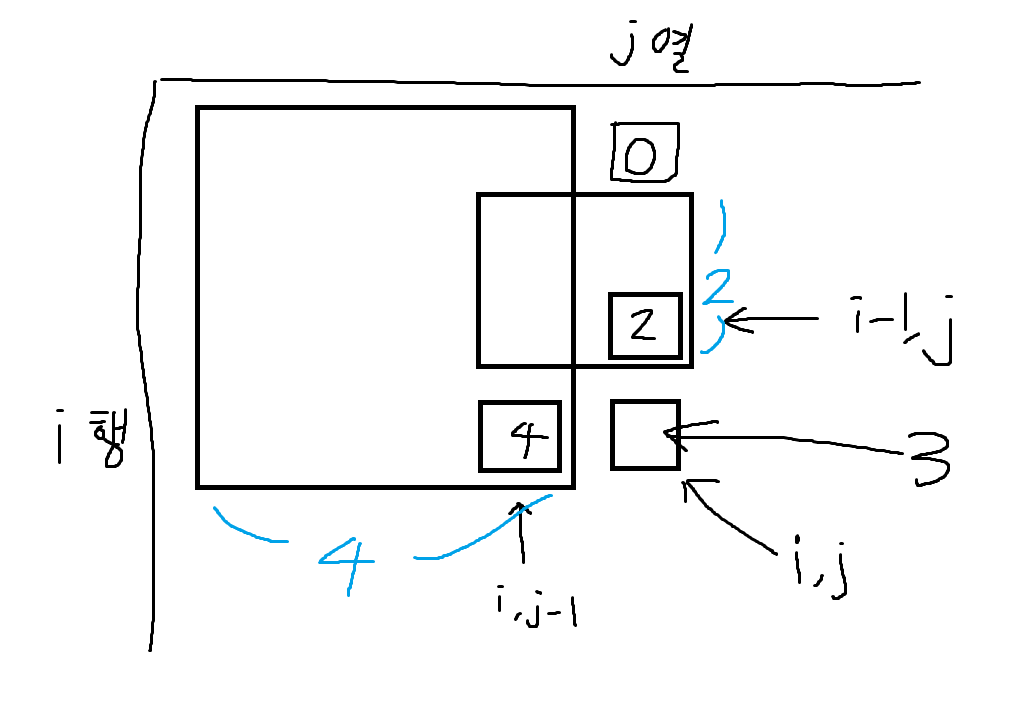
이 쪽이 좀 더 쉽다. 예를 들어, 왼쪽이 4고 위가 2라고 하자. 그러면 구역에 모두 포함되므로 i,j를 포함한 3x3 정사각형은 무조건 만들 수 있다. 그리고 위가 2라는 제약이 있으므로, 4 이상은 만들 수 없다.
즉, 둘 중 더 작은 값 + 1 사이즈의 정사각형을 만들 수 있다.
이걸 matrix를 순회하면서 돌리고, 다 돌린 뒤에 모든 값을 합하면 답이 나온다.
코드(Python3, Accepted, 409ms(상위 0.55%), 18.71MB(상위 19.61%))
if matrix[i][j] and matrix[i-1][j] and matrix[i][j-1]: 부분의 의미는, 셋 중 하나라도 0이면 통과 안 된다는 의미이다. matrix[i][j] 본인이 0이면 당연히 그대로 0이고, 1이라고 하더라도 바로 왼쪽이나 바로 위에 0이 있으면 2x2 이상의 정사각형을 만들 수 없다.
그 밑에 있는 if-else문은, 위의 풀이에서 나온 2가지 경우이다.
바로 왼쪽과 위의 값이 같으면, 그 값을 size로 하고, matrix[i-size][j-size]가 1일 경우 size+1 사이즈의 정사각형을 만들 수 있다. 0이면 그냥 size 사이즈만 만들 수 있다.
바로 왼쪽과 위의 값이 다르면, 둘 중 더 작은 값 + 1 만큼의 정사각형을 만들 수 있다.
class Solution:
def countSquares(self, matrix: List[List[int]]) -> int:
n, m = len(matrix), len(matrix[0])
for i in range(1, n):
for j in range(1, m):
if matrix[i][j] and matrix[i-1][j] and matrix[i][j-1]:
if matrix[i-1][j] == matrix[i][j-1]:
size = matrix[i-1][j]
if matrix[i-size][j-size]:
size += 1
matrix[i][j] = size
else:
matrix[i][j] = min(matrix[i-1][j], matrix[i][j-1]) + 1
answer = sum(sum(row) for row in matrix)
return answer챌린저 문제 : 도둑질
풀이 접근
사이즈가 커서 주먹구구식 풀이로는 통과가 안 되니 난이도를 높게 책정한 듯 하다. 집이 최대 100만개나 있고, 효율성 테스트까지 제대로 있는 문제인 만큼 시간의 압박이 있다. 하지만 그것까지 고려해도 미들러보다 훨씬 쉬운 문제이다.
정직하게 dp로 풀린다. 다만 원형이므로 약간의 테크닉이 필요하다.
코드(Python3, 통과, 최대 641.39ms, 40.3MB)
1부터 n-2까지만 순회를 할 것이다. 0번과 마지막 n-1번은 서로 맞닿아 있어 서로 영향을 주기 때문에 경우를 나눠야 하기 때문이다.
a,b,c,d는 각각 다음과 같다.
a : money[0]을 털었고, 마지막 집을 털었을 경우
b : money[0]을 털었고, 마지막 집을 안 털었을 경우
c : money[0]을 안 털었고, 마지막 집을 털었을 경우
d : money[0]을 안 털었고, 마지막 집을 안 털었을 경우
맨 처음(money[0]만 털지 안 털지 결정한 후)에는, b와 c 경우는 불가능하므로, 불가능하다는 의미에서 dp에서 어차피 배제될만큼 작은 값을 넣어둔다. (보통 -inf로 표현한다)
그 뒤에는, 1번 집부터 n-2번 집까지 순회하면서, 값을 갱신한다. a와 c는 각각 b와 d로부터 마지막 집을 턴 경우에만 실현 가능하므로, 각각 b + money[i]와 d + money[i]가 되고, b는 a,b로부터, d는 c,d로부터 마지막 집을 안 턴 경우에 실현 가능하므로, 둘 중 더 큰 값으로 갱신해 준다.
이렇게 순회를 끝마치고, 마지막(n-1번) 집을 털 수 있는 경우는 d 뿐이므로, answer를 낼 땐 d에만 money[n-1]을 더해준다.
def solution(money):
a, b, c, d = money[0], -1001, -1001, 0
for i in range(1, len(money) - 1):
a, b, c, d = b + money[i], max(a, b), d + money[i], max(c, d)
answer = max(a, b, c, d + money[-1])
return answer