99클럽(2기) 코테 스터디 17일차 TIL (K-th Smallest Prime Fraction)

---

99클럽 코테 스터디

나의 마지막 TIL이다. 취업이 되어서 오늘부터 띵까띵까 놀 것이기 때문에...
그래도 면접 합격 소식 보기 전에 푼 거라 오늘의 TIL은 마지막으로 작성하려 한다.

O(nlogn)으로 풀려면 꽤나 빡센 문제였다. 그래서 오늘도 한 문제만 TIL 작성했다.

챌린저 문제 K-th Smallest Prime Fraction : https://school.programmers.co.kr/learn/courses/30/lessons/43236

출처 : leetcode

---

챌린저 문제 : K-th Smallest Prime Fraction

---

풀이 접근

그냥 무식하게 풀면 O(n^2)로도 풀리긴 풀린다. 하지만, 오늘의 주제가 이분탐색이기도 하고,

Follow up: Can you solve the problem with better than O(n2) complexity?

라고 대놓고 문제에 써 있기 때문에, O(nlogn)으로 줄일 방법을 이분탐색을 활용해 찾아보았다.

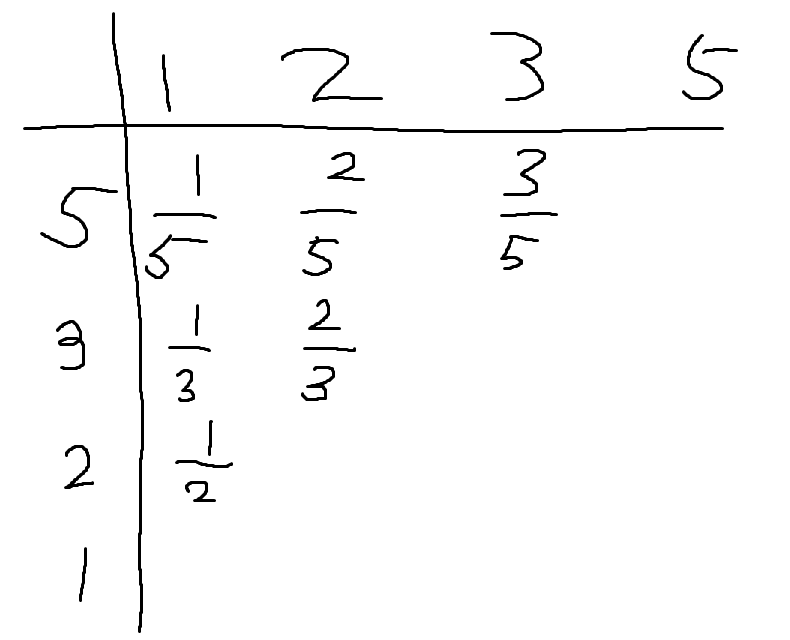
문제의 Example 1을 위와 같은 표로 그릴 수 있다. 1,2,3,5를 분자로, 5,3,2,1을 분모로 하는 것이다. 이렇게 만들면 n(n-1)/2개의 분수가 나온다. 그리고, 행으로 보나 열로 보나 정렬되어 있다. 하지만, 이 전체는 순서 보장이 된 방식이 없는데, 어떻게 이분탐색으로 풀 수 있는 것인가? 단순히 싹 모아다 정렬하면 O(n^2)도 아닌 아예 O(n^2logn)이 되어버릴 것이다. 따라서 다음과 같은 풀이를 생각했다.

p/5(5는 위의 예시 기준이고, 주어진 소수 중 가장 큰 수로 한다)보다 작거나 같은 분수의 개수를 O(n)에 세고, 그 개수가 k보다 큰 최소의 소수 p를 O(logn)번의 시도로 찾으면, O(nlogn)의 풀이가 된다.

우선 p를 O(logn)번의 시도로 찾는 건 이분 탐색을 적용할 수 있다. p/d (나는 d를 소수 중 최댓값으로 썼다)보다 작은 분수의 개수는 p의 대소관계와 같기 때문이다.

그렇다면, p/d보다 작거나 같은 분수의 개수를 O(n)에 어떻게 찾는가?

위의 표를 보자. 분수는 같은 행에서는 왼쪽으로 갈수록 작아지고, 같은 열에서는 밑으로 갈수록 커진다.

따라서, 예를 들어 3/5보다 작은 분수의 개수를 찾으려 한다면, 다음과 같이 할 수 있다.

• 3/5은 1행 3열이다. [1,2,3,5]를 기준으로 한다면 분모의 인덱스는 3, 분자의 인덱스는 2이다.
• 3/5는, 3/5과 같으므로, 그보다 왼쪽에 분수는 모두 3/5보다 작고, 오른쪽은 모두 3/5보다 크다.
• 즉, 1행에서 3/5보다 작거나 같은 분수는 3개이다(스스로를 포함).

• 그 다음은 1행(분모가 3, 또는 분모의 인덱스가 2)으로 내려간다.
• 3/5에서 그대로 내려가면 3/3으로, 3/5보다 크다. 그러므로 왼쪽으로 간다.
• 3/3에서 왼쪽으로 가면 2/3으로, 3/5보다 크다. 그러므로 또 왼쪽으로 간다.
• 1/3은 3/5보다 작다. 그리고 방금 전 2/3는 3/5보다 크므로, 3/5보다 작은 분수의 개수는 1/3의 인덱스+1인 1이 된다.
• 즉, 2행에서 3/5보다 작은 분수는 1개이다.

마지막으로, 1/3에서 한 칸 내려간 1/2에서 마찬가지로 3/5보다 작음을 확인하고, 3행에서 3/5보다 작은 분수의 개수로 1개를 더할 수 있다.

-> 3/5보다 작거나 같은 분수가 5개임을 알 수 있다.

이 순회 과정은, 왼쪽과 밑으로만 내려가므로, 최대 2n-2번밖에 진행할 수 없다. (맨 오른쪽 위에서 맨 왼쪽 밑까지) 따라서 시간복잡도 O(n)이 된다.

마찬가지 과정으로, 2/5보다 작거나 같은 분수가 3개임을 알 수 있다. 이는 2/5가 3번째로 작은 분수라는 의미이므로, 답은 그대로 [2,5]가 된다.

근데 만약, Example 1에서 k=4이면 어떻게 되는가?

이 때는, k가 (2/5보다 작거나 같은 분수의 개수)보다 크고, (3/5보다 작거나 같은 분수의 개수)보다 작다. 그러므로, 답은 2/5보다 크고 3/5보다 작은 분수가 되어야 한다. 이러한 분수를 전부 후보 리스트에 넣는다.

그 방법은, 위의 순회 과정애서 3/5를 기준으로 비슷하게 순회하되, 각 행에서 3/5보다 작은 최대의 분수에서 멈추지 않고, 조금 더 임시로 왼쪽으로 가면서 2/5보다 큰 분수를 전부 후보에 넣는다.

2/5와 3/5이라는 예시는 여기에는 해당되지 않지만, 예를 들어 [1,2,3,5,7,17,97,113]을 탐색한다면, 17/113과 97/113 사이에 2/7, 3/7, 5/7 세 분수가 있듯이 여러 분수가 있을 수도 있기 때문이다.

다만, 2/7까지 들어갔다고 해서 그 밑인 2/5로 내려가는 게 아니라, 원래 순회 기준인 5/7에서 한 칸 밑인 5/5로 내려가고 거기서 또 왼쪽으로 임시 순회를 하는 것이다. (이렇게 해야 3/5을 놓치지 않을 수 있다)

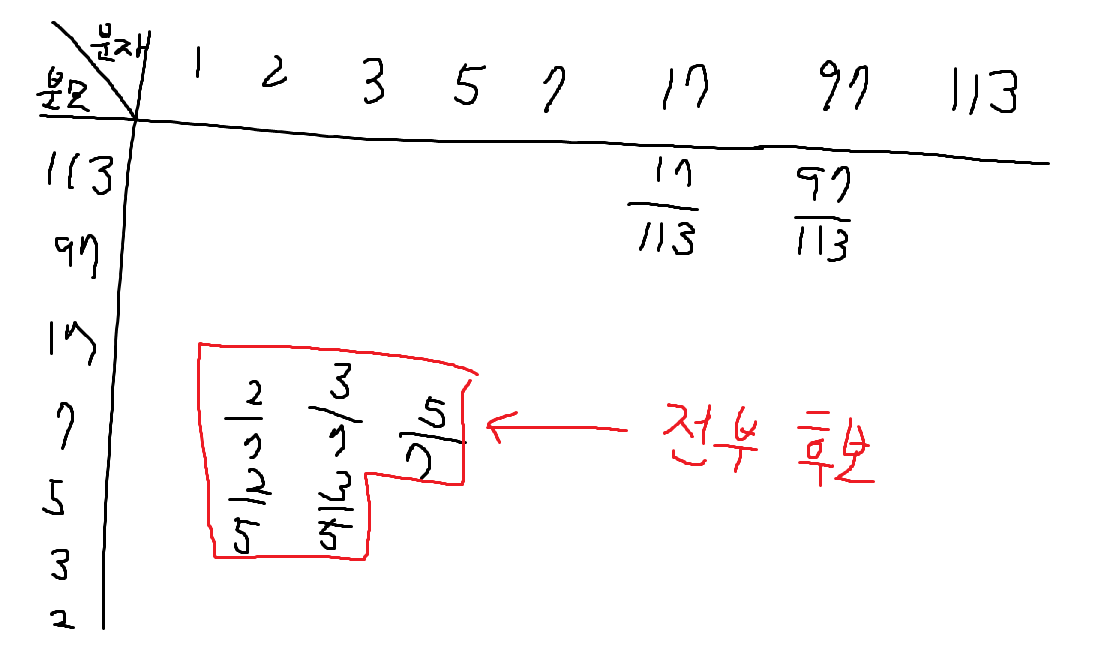
그림으로 보면 위와 같다. 주어진 k가 (17/113보다 작거나 같은 분수의 수)보다 크고, (97/113보다 작거나 같은 분수의 수)보다 작다면, 찾는 답은 17/113보다 크고 97/113보다 작은 분수일 것이다.

이를 찾기 위해, 97/113에서 출발해서 한 칸씩 밑으로 내려가면서 각 행에 17/113보다 크고 97/113보다 작은 분수가 있으면 전부 후보로 넣어야 하는데, 한 행에 후보가 여러 개 있을 수도 있으므로 한 개만 넣어서는 안 되고(0개일 수도 있다), 여러 후보(2/7,3/7,5/7)를 넣은 뒤에는 가장 작은 후보(2/7)가 아닌 가장 큰 후보(5/7)에서 다음 행으로 내려가서 (5/5에서부터 마찬가지로 왼쪽으로) 탐색해야 된다는 것이다.

---

코드(Python3, Accepted, 46ms(상위 0.1%), 16.76MB(상위 9.61%))

leetcode에서 푼 문제 중에 상위 0.1%는 처음이다. 아주 좋은 결과라 만족스럽다.

d는 주어진 소수 중 가장 큰 수이다.
여기서 num, 또는 den으로 시작하는 모든 변수는 numerator(분자)의 arr의 index, 그리고 denominator(분모)의 arr의 index이다. [1,2,3,5]에서 분수 3/5를 나타내면, num은 2, den은 3인 것이다.

order_of_fraction(n)은, arr[n] / d보다 작거나 같은 분수의 개수를 return하는 함수이다. 실행하는 데에 O(n)의 시간복잡도를 가진다.

그리고, 이분탐색을 진행하는데, 이 이분탐색의 목표는 arr[num]/d가 k번째 분수보다 크거나 같은 최소의 num을 찾는 것이다.

이를 위해, num_left를 0, num_right를 n-2(어차피 n-1로 하면 분자가 d인 조건에 맞지 않는 분수이다)로 하고, 그 둘의 중간인 num_mid에 대해서 arr[num_mid]/d가 몇 번째 분수인지(=order) 센다.

• order가 k와 정확히 같으면, arr[num_mid]/d가 바로 정답이 된다.
• order가 k보다 크면, arr[num_mid]/d보다 작은 어떤 분수가 답이 된다.
• order가 k보다 작으면, arr[num_mid]/d보다 큰 어떤 분수가 답이 된다.

무한루프에 빠지지 않으면서, 효율적으로 이분탐색하기 위해, order가 k보다 작을 땐 num_left를 num_mid가 아닌 num_mid + 1로 올려준다. 어차피 num_mid는 k번째 분수보다 작으므로, 더 고려할 필요가 없기 때문.

이렇게 이분탐색하는데에는, logn번의 시도가 필요한데, 각 시도마다 O(n)인 order_of_fraction 함수를 실행하므로, O(nlogn)의 시간복잡도를 가지게 된다.

그리고...

이렇게 이분탐색이 종료되면, (num_right와 같아진) num_left가 찾던 num이 된다.

라고 착각하면 테스트케이스에 걸린다. 잘 생각해 보면, (2번째로 큰 소수) / (가장 큰 소수)는 가장 큰 분수라는 보장을 할 수 없다. 즉, num_left = n-2인 채로 종료되었는데, 알고 보니arr[n-2]/d보다 더 큰 분수를 찾아야 될 수도 있다는 의미이다.

그래서 order_of_fraction 함수에 num_left를 넣고 다시 실행시켜서 k와의 대소관계부터 잡고 간다.

• order가 k와 정확히 같으면, arr[num_left]/d가 바로 정답이 된다.
• order가 k보다 크면, arr[num_left]/d보다 작은 어떤 분수가 답이 된다.
• order가 k보다 작으면, arr[num_left]/d보다 큰 어떤 분수가 답이 된다.

다만, 여기서는 order가 k보다 작은 특수한 경우만 따로 순회 방식을 달리해서 arr[n-2]/d보다 큰 분수들을 찾고, 그렇지 않을 때는 arr[num_left]/d보다 작고 arr[num_left-1]/d보다는 큰 분수들을 풀이 접근 마지막에 설명한 대로 찾아서 candidates 리스트에 넣는다.

그리고 이 candidates를 분수의 크기 순으로 sort하고, 정확히 k번째가 무슨 분수인지 k - order - 1번째로 찾는다. 놀랍게도, k-order-1은 order가 k보다 큰 경우와 작은 경우 모두 유효한 index이다.

분수의 값만 가지고는 분자, 분모를 역산하기 번거로우므로, candidates 리스트에 값을 넣을 때 애초에 (분수의 값, 분자(의 인덱스), 분모(의 인덱스))의 튜플 형태로 집어넣어 주면 된다.

class Solution:
    def kthSmallestPrimeFraction(self, arr: List[int], k: int) -> List[int]:
        n = len(arr)
        d = arr[n - 1]
        num_left = 0  # number가 아니고 numerator(분자)임
        num_right = n - 2


        def order_of_fraction(numerator):  # numerator 분자, 시작 시 분모는 제일 큰 수 고정
            num = numerator
            order = 1
            for den in range(n-1, 0, -1):  # denominator 분모
                while num >= 0 and arr[num] * d >= arr[numerator] * arr[den]:
                    num -= 1
                if num < 0:
                    return order
                order += num + 1
            return order


        while num_left < num_right:
            num_mid = (num_left + num_right) // 2
            order = order_of_fraction(num_mid)
            if order == k:
                return [arr[num_mid], d]
            if order > k:
                num_right = num_mid
            else:
                num_left = num_mid + 1

        order = order_of_fraction(num_left)

        if order == k:
            return [arr[num_left], d]
        elif order < k:
            candidates = []
            for den in range(n - 2, 0, -1):
                num = den - 1
                while num >= 0 and arr[num] * d > arr[num_left] * arr[den]:
                    candidates.append((arr[num] / arr[den], num, den))
                    num -= 1
        else:
            num = num_left
            candidates = [(arr[num] / arr[n - 1], num, n - 1)]
            for den in range(n - 1, 0, -1):
                while num >= 0 and arr[num] * d >= arr[num_left] * arr[den]:
                    num -= 1
                if num < 0:
                    break
                num_temp = num
                while num_temp >= 0 and arr[num_temp] * d > arr[num_left - 1] * arr[den]:
                    candidates.append((arr[num_temp] / arr[den], num_temp, den))
                    num_temp -= 1

        candidates.sort()
        answer = [arr[candidates[k - order - 1][1]], arr[candidates[k - order - 1][2]]]
        return answer

---