99클럽 코테 스터디
오늘부터 비기너, 미들러, 챌린저 문제를 다 풀어보기로 했다. -> 이 TIL 끝까지 쓰고 추가하는 건데, 문제푸는건 괜찮은데 TIL이 매우 오래걸린다. 힘들다...
월,목 정기모임 시간에도 시간 내로 셋 다 풀고 TIL 작성을 목표로 하고, 가능하면 자바로까지 풀어보려고 한다. 자바 재활이 필요하다.
비기너나 미들러 문제도 통과만을 목적으로 하지 않고 더 효율적인 방법을 추구하면 꽤 생각할 게 많을 때도 있는 것 같다. 문제 난이도 자체도 역전되어 있는 경우도 종종 있고(오늘은 그렇진 않은 것 같다).
오늘의 문제는 공통적으로, 논리적 사고로 접근할만한 문제이다. 브루트포스 기법으로도 풀리긴 하지만, 뇌를 비우고 완전탐색으로만도 풀리는 건 오히려 미들러, 챌린저이고, 비기너는 생각이 필요하다.
하지만 미들러, 챌린저 문제도 더 효율적으로(입력 자료의 크기가 더 늘어나도 풀 수 있도록) 풀려면 생각이 좀 더 필요하다.
비기너 문제 최소직사각형 : https://school.programmers.co.kr/learn/courses/30/lessons/86491
미들러 문제 카펫 : https://school.programmers.co.kr/learn/courses/30/lessons/86491
챌린저 문제 모음사전 : https://school.programmers.co.kr/learn/courses/30/lessons/86491
출처 : 프로그래머스
비기너 문제 : 최소직사각형
풀이 접근
어제에 이어서 논리적 사고로 풀이 접근을 열심히 하면 코드 자체는 짧게 나오는 문제들이 많다.
이번 문제도 그렇다. 명함들을 90도 회전시켜 가로로 길게 두거나 세로로 길게 두는 게 자유이다. 따라서 지갑의 최대 크기가 가로 w, 세로 h이면, 가로가 더 길거나 같다고 가정해도 문제없다(세로가 더 길면 지갑과 모든 명함을 90도 돌려 눕히면 되니까). 그러면 이 w에 대해서 말인데...
w는 sizes의 모든 원소(명함)들의 원소(가로,세로 길이)들 중 최댓값이다.
왜? 제일 긴 명함이 딱 맞게 들어가려면 w여야 하니까.
그 다음은, 모든 명함을 가로가 길고 세로가 짧도록 눕힌다. 왜? w를 정하고 나면 h는 모든 명함의 세로 길이 중 최댓값이니까.
이 과정을 거치고 나면 알 수 있는 것이, w는 모든 명함들의 가로,세로 중 더 긴 길이의 최댓값이고, h는 모든 명함들의 가로,세로 중 더 짧은 길이의 최댓값이 된다.
따라서, 모든 명함의 길이를 정렬하고, 각 명함의 긴 길이 중 최댓값과 짧은 길이 중 최댓값을 따로 구해서 곱하면 된다.
코드(Python3, 통과, 2.28ms, 11.2MB)
코드는 되게 짧다.
sizes를 sort하면 안된다는 점에 유의한다. sizes의 각 원소인 [w,h]를 sort하는 것이다.
max(size[0] for size in sizes)는 각 명함의 더 짧은 길이 중 최댓값이고,
max(size[1] for size in sizes)는 각 명함의 더 긴 길이 중 최댓값이다.
def solution(sizes):
for size in sizes:
size.sort()
return max(size[0] for size in sizes) * max(size[1] for size in sizes)미들러 문제 : 카펫
풀이 접근
브루트포스로 풀라고 자로 잰 듯이 낸 문제이다. 다만 수학교육과의 고질병으로 연립이차방정식으로 풀 수 있는 문제를 굳이 안 쓰고 브루트포스로 비효율적으로 풀기 싫어졌다.
코드의 효율성 말고 풀이하는데 걸리는 시간으로 치면 브루트포스가 훨씬 쉽지만, brown을 최대 1억으로, yellow를 최대 1경으로 늘린다면? 브루트포스로는 못 푼다. 그리고 나는 그럴 때를 항상 대비해서 최적의 효율로 문제를 푸는 데 주력하는 편이다. (그런 면에서 프로그래머스는 정확성 판단만 있고 효율성 판단이 없는 문제도 많고, 실행속도나 메모리 순위도 접근성이 높지 않아 백준에 비해 살짝 아쉽다.)
서론이 길었는데, brown을 b, yellow를 y, 가로를 w, 세로를 h (이 문제는 w>=h라는 조건을 줬다)라 하자.
문제의 조건에 따르면, wh = b+y이다. (전체 카펫의 넓이)
또한, w + h - 2 = b/2이다. (테두리의 넓이의 절반)
이걸 대입법으로 연립하고, w나 h에 대한 이차방정식으로 풀면,
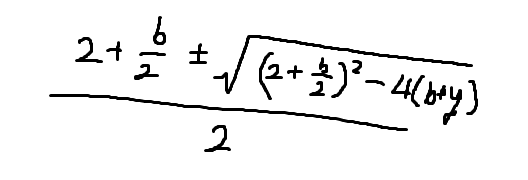
요게 나온다. 가로가 세로보다 길거나 같으므로, +는 w이고, -가 h가 된다. b와 y를 대입해서 답을 내기만 하면 되는 것이다. 코딩이 아니라 수학 문제처럼 풀어버렸는데, 그래도 여기서 약간의 테크닉이 필요하긴 하다.
코드(Python3, 통과, 0.02ms, 10.4MB)
여기서 테크닉이란, math 라이브러리를 안 쓰면 파이썬은(그리고 아마 대부분의 프로그래밍 언어는) 정수의 제곱근을 정수로 제대로 구해주지 못할 때가 있다는 것이다. 9**0.5 하면 3이 안나오고 2.9999가 나온다던지? 그래서 여기다가 int()를 씌워도 3이 아닌 2를 뱉어버리는 것이다.
나는 이럴 때 쓰는 방법이 있는데, 1을 더해서 제곱근(**0.5)을 취하고 int를 씌워서 소수점 아래를 버린다. 이러면 9가 아닌 10의 제곱근이니 3.xx가 나오고, 소수점 아래를 버리면 정상적으로 3이 나온다. 0에다가 1 더하고 제곱근 씌웠다가 1 되어버리는 불상사는 배제하기 위해 제곱근 안의 수가 0일 때만 따로 한다.
물론 여기서는 문제의 조건상 반드시 정수가 나온다는 보장이 있으니까 쓸 수 있는 방법이다.
discriminant는 판별식이라는 뜻으로, 이차방정식에서는 b제곱 - 4ac이다(중학교 때 달달 외웠던 기억이 날 수도 있다).
위에 있는 이차방정식의 근의 공식에서 2로 나누는 건 맨 마지막에 해야 한다. 안 그랬다간 또 정수가 아닌 실수로 0.5(의 탈을 쓴 0.4999라던가)끼리 더하다가 불상사가 생길 수 있다.
def solution(brown, yellow):
answer = [2 + brown // 2] * 2
discriminant = answer[0] ** 2 - 4 * (brown + yellow)
if discriminant:
root = int((discriminant + 1)**0.5)
answer[0] += root
answer [1] -= root
answer[0] //= 2
answer[1] //= 2
return answer챌린저 문제 : 모음사전
풀이 접근
이 문제도 브루트포스로 모든 단어를 만들어 놓고(3906개밖에 안 된다) 그냥 편하게 인덱스로 셀 수도 있다. 근데, 미들러 문제에서도 그랬지만, 이 방법은 단어 길이가 12(단어가 2억개가 넘는다)만 돼도 못 쓴다.
단어 길이가 12인게 그닥 비정상적인 상황도 아닌데, 이 정돈 해결 가능해야 되지 않겠는가? 라고 생각한다.
따라서, 여기서도 경우의 수 파악으로 풀어보았다.
예를 들어, 'AEIOU'라는 단어는 몇 번째일까? 이를 알기 위해서는, 사전에서 단어를 찾을 때 인간이 사고하는 방식대로, 단어의 맨 앞글자부터 분석해야 한다.
맨 앞글자 'A'는 모음 5개 중 1번째로, 이보다 앞에 오는 글자가 없다. 따라서 맨 앞글자가 다르면서 AEIOU보다 빨리 오는 단어는 없다. 다만 단어 'A'는 AEIOU보다 빨리 오므로, answer에 1을 더한다. (만약 찾으려는 단어가 'A'였어도, 1을 더해도 된다. 왜냐면 'A'가 첫 번째 단어이므로 답이 1인데, 그 1을 더하는 것이다)
A로 시작하고 다음 글자에 따라서 AEIOU보다 빨리 오는 단어가 있을 수도 있지만, 그걸 찾는 건 두 번째 글자를 분석할 때 하는 게 정확하므로, A까지 분석했을 때는 answer를 1까지만 늘리고 멈춘다.
그 다음 글자 'E'는 모음 5개 중 2번째로, 앞에 A가 온다. 따라서, 'AA'로 시작하는 모든 가능한 단어는 AEIOU보다 빨리 온다.
그 전에 우선, 'AE'는 반드시 AEIOU보다 빨리 오므로, 그냥 1을 더한다. 여기까지 했을 때 눈치챘을 수도 있겠지만, 어떤 단어든 그 단어를 앞에서부터 몇 글자 자른 것은 고정적으로 존재하므로, 각 글자마다 answer가 1씩은 고정적으로 더해진다.
그래서 answer는 2가 됐고, 여기서부터가 중요한데, 'AA'로 시작하는 모든 가능한 단어는 몇 개인가? 여기서는 음... 코딩테스트 기법이라기보다는 그냥 수열의 일반항 찾기에 가깝다. 수학적 귀납법으로 접근 가능한데, 'AA'로 시작하면 뒤에 3글자가 빈다.
이걸 찾기 전에, 'AAAAA'로 시작하는 단어는 몇 개일까? 당연히 한 개다.
'AAAA'로 시작하는 건? 여기까진 셀 만하다. 6개(5개 아니다, AAAA, AAAAA, AAAAE, AAAAI, AAAAO, AAAAU 6개)
그럼 'AAA'로 시작하는 건? 'AAA' 한 개, 'AAAA'로 시작하는 거 6개, 'AAAE'로 시작하는 거 6개, 'AAAI'로 시작하는 거 6개, AAAO 6개, AAAU 6개, 총 31개다. 여기서 알 수 있는 사실?
특정 n글자로 시작하는(뒤에 k칸이 빈) 단어의 총 개수는 n+1글자로 시작하는(뒤에 k-1칸이 빈) 단어의 총 개수의 5배에 1을 더한 것이다.
인덱스상 뒤에 몇 글자가 남았는지를 세는 게 빠르므로, 나는 tail = [1, 6, 31, 156, 781]로 두었다. tail[k]는 뒤에 k글자가 빈 단어가 주어졌을 때, 그 단어로 시작하는 단어의 총 개수이다. 이렇게 수열의 일반항을 구해놓으면(앞 원소에 5곱하고 1더해서 구해도 되고, 앞 원소에 5의 거듭제곱을 더해서 구해도 된다), 단어 길이가 5건 50이건 5000이건 풀 수 있다. (5천이면 정수의 크기가 너무 커지는 게 문제가 될 수는 있다)
다시 돌아와서, 'AA'로 시작하는 단어는 tail[3] = 156개이다. 따라서 'AEIOU'의 두 번째 글자까지 분석했을 때 answer는 158이다.
세 번째 글자 'I'는 5개 중 3번째인데, 일단 'AEI' 단어 자체는 고정이므로 마찬가지로 answer에 1을 고정으로 더하고, 'AEA'로 시작하는 단어 31개, 'AEE'로 시작하는 단어 31개를 더해준다. 그래서 answer는 221이 되었다.
네 번째 글자 'O'도, 'AEIO' 단어를 세어 answer에 1을 더해주고, 'AEIA'로 시작하는 단어 6개, 'AEIE'로 시작하는 단어 6개, 'AEII'로 시작하는 단어 6개, 총 18개를 또 더해준다. answer는 240.
마지막 글자에서도, 'AEIOU'를 세서 1, AEIOA,AEIOE,AEIOI,AEIOO 4개를 또 더해서 최종 answer는 245가 된다.
여기서 알 수 있는 사실?
'ㅁㅁ△ㅁㅁ'보다 앞에 오는 단어를 셀 때, △를 기준으로 삼으면, △ 뒤에 있는 글자 수를 k라 하고, △가 5개의 모음 중 n번째일 때, 'ㅁㅁ△' 한 개에 더해, (n-1) * tail[k]개가 더해진다.
위에 써 두었듯 tail = [1, 6, 31, 156, 781]이다. 이제 이걸 코드로 쓰기만 하면 된다. 풀이를 말로 풀어쓰면 엄청 복잡하고 길어보이는데, 코드로는 막상 그렇지도 않다.
코드(Python3, 통과, 28ms, 17.20MB)
alp[알파벳]은 그 알파벳보다 사전순으로 빠른 모음의 수이다.
tail[k]는 (5-k)글자짜리 단어로 시작하는 단어의 수이다.
단어가 주어지면, 단어의 각 글자를 순회하면서,
그 글자까지로 자른 단어 한 개로 answer += 1을 해 주고,
그 글자를 더 빠른 모음으로 바꿨을 때 가능한 모든 단어의 수, 즉 그 알파벳보다 사전순으로 더 빠른 모음의 수(alp[word[i]])에 그렇게 바꾼 단어로 시작하는 모든 단어의 수(tail[4 - i])를 곱해서 answer에 더해준다.
끝! 이 방법이라면 글자 수를 늘려도 풀 수 있고, 모음이 아니라 26개 알파벳을 다 써도 tail의 일반항 구하는 방식만 5에서 26으로 바꿔서 풀 수 있다.
def solution(word):
alp = {'A' : 0, 'E' : 1, 'I' : 2, 'O' : 3, 'U' : 4}
tail = [1, 6, 31, 156, 781]
answer = 0
for i in range(len(word)):
answer += 1
answer += alp[word[i]] * tail[4 - i]
return answer