99클럽 코테 스터디
굉장히 빡셌다. 두개 푸는데 합 2시간이 걸렸고, 실행시간도 썩 만족스럽지 않은 결과였다.
빨리 풀고 풀이가 맘에 들면 신나서 TIL을 자세히 작성하는데, 오늘은 그냥 간략하게만 적어보았다...
1번 문제 억억단을 외우자 : https://school.programmers.co.kr/learn/courses/30/lessons/138475
2번 문제 숫자 타자 대회 : https://school.programmers.co.kr/learn/courses/30/lessons/136797
출처 : 프로그래머스
1번 문제 억억단을 외우자
풀이 접근
표에 어떤 수가 몇 번 나오는지는 그 수의 약수의 개수만큼 나온다.
시간 최적화를 위해, 필요한 최소한만큼만 계산해야 한다.
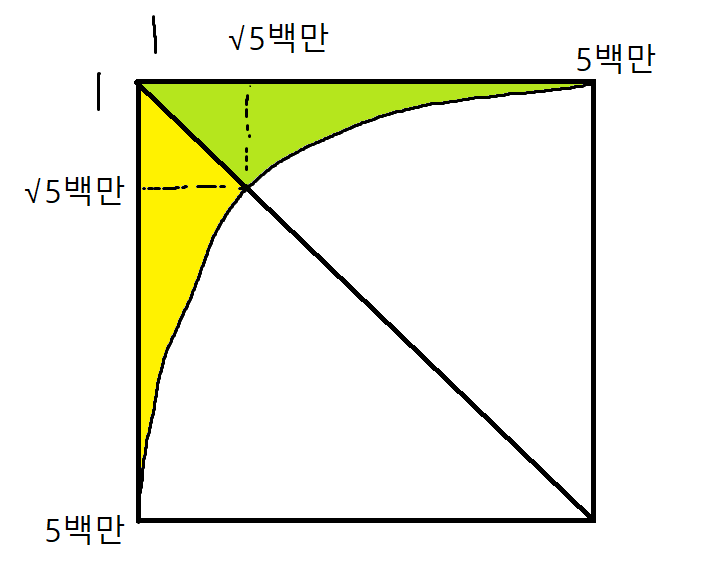
아래 그림에서 초록색 부분에 들어있는 것들만 세고, 2배를 해 줘서 대각선을 기준으로 선대칭인 부분(노란색 부분)의 개수를 직접 세지 않고 맞춘다. 그리고 대각선에 정확히 놓여 있는 수(제곱수)들은 중복해서 세지 않도록 1씩 빼고, 테두리에 있는 1단은 세지 않도록 처음부터 모든 수의 약수를 2개씩 두고 2단부터 센다.
코드 (Python3, 통과, 최대 4627.60ms, 91.3MB)
yaksu[n]은 n의 약수의 개수이다.
most_num[n]은 n 이상 e 이하의 수 중 가장 약수의 개수가 많은 수이다(문제에서 요구하는 수).
수학적으로 더 좋은 풀이가 있을 것 같은데 그것까지 찾기엔 오늘은 너무 피곤쓰... 일단 통과한 걸로 만족 중이다.
def solution(e, starts):
yaksu = [2] * (e+1)
yaksu[1] = 1
for n in range(2, e+1):
if n*n > e:
break
for m in range(n, e//n + 1):
yaksu[n*m] += 2
yaksu[n*n] -= 1
most_num = [0] * (e+1)
p = e
most = 0
num = 0
while p:
if yaksu[p] >= most:
num = p
most = yaksu[p]
most_num[p] = num
p -= 1
answer = [most_num[i] for i in starts]
return answer2번 문제 숫자 타자 대회
풀이 접근
dp 문제이다. (dp가 아닌 방법으로는 못 풀 것 같다.)
그... 커넥션 프로파일을 이용한 dp 비스무리하게 푼 것 같다.
근데 생각나는대로 급조한 방식이라 그런지 dp를 구현한 방식이 깔끔하지 않다고 느껴진다.
(반대로 코스트를 하드코딩한건 만족스럽다. 무조건 성능이 개선되니까)
원래 좀 재귀적으로 나와야 되는데, 이 코드에서는 구차하게? 직전 dp를 따로 떼서 뒀다가 새 dp를 다시 만든다.
코드 (Python3, 통과, 최대 966.18ms, 11.3MB)
cost[n][m]은 n번 자판에 있던 손가락을 m번 자판으로 옮겨 클릭하는 데 드는 비용이다.
매번 직전에 클릭한 숫자를 click으로 두고, dp[n]은 click 이외의 다른 손가락이 n번 자판에 위치할 때 드는 최소 비용이다. (두 손가락이 겹치지 않는다는 조건이 있으므로 dp[click]은 항상 inf로 둔다.)
초기 조건은 click을 4로 두고, dp[6]만 0으로 두고, 나머지 상황은 불가하므로 inf로 두면 된다. (click을 6으로 두고 dp[4]를 0으로 둬도 똑같다.)
click, i 두 개의 자판에 손가락이 올라가 있는 상태에서 다음번에 c번 자판을 누르려면 click->c일 수도 있고 i->c일 수도 있다.
즉 c번 자판을 누르고 나면 c,i에 손가락이 있거나 c, click에 손가락이 있거나 둘 중 하나다. 이는 dp[i] 상태에서 c번 자판을 누르면 dp[i], dp[click] 두 상태가 가능하다는 것이다. 그리고 가능한 상태 중 최소비용의 상태를 찾아야 하므로, 0~9번 자판을 돌면서 가능한 상태를 저장해 두고, 그 중 최소비용을 새로운 dp로 재정의한다.
쓰다보니 풀이 해설을 여기다 써버린 느낌이 드는데 대충 넘어가겠다.
tmi) inf는 700001이면 충분한데 0 하나를 실수로 더 넣었다.
def solution(numbers):
cost = [
[1,7,6,7,5,4,5,3,2,3],
[7,1,2,4,2,3,5,4,5,6],
[6,2,1,2,3,2,3,5,4,5],
[7,4,2,1,5,3,2,6,5,4],
[5,2,3,5,1,2,4,2,3,5],
[4,3,2,3,2,1,2,3,2,3],
[5,5,3,2,4,2,1,5,3,2],
[3,4,5,6,2,3,5,1,2,4],
[2,5,4,5,3,2,3,2,1,2],
[3,6,5,4,5,3,2,4,2,1]
]
clicks = [int(numbers[i]) for i in range(len(numbers))]
click = 4
inf = 7000001
dp = [inf] * 10
dp[6] = 0
for c in clicks:
next_dp = [set() for _ in range(10)]
for i in range(10):
next_dp[i].add(dp[i] + cost[click][c])
next_dp[click].add(dp[i] + cost[i][c])
for i in range(10):
if i == c:
dp[i] = inf
else:
dp[i] = min(next_dp[i])
click = c
answer = min(dp)
return answer