숭실대학교 알고리즘 코딩테스트 합격반

김소희·2023년 8월 21일

숭실대학교 알고리즘 코딩테스트 합격반에 지원했는데 합격하여
8월 21일부터 9월 7일까지 3주간 수업을 들을 수 있게 되었다.

나는 이 수업을 계기로 파이썬을 처음 접하게 되었는데
파이썬을 모르기 때문에 오히려 정답을 푸는 방식만 알고 정답을 보지 않기 때문에
나중에 내가 직접 자바로 풀어 볼 수 있어서 좋았다.

발상의 전환을 잘하는 사람들의 간결한 코드를 보면 감탄할 때가 많은데
나도 수학적 사고력을 향상해서 간결하고 성능 좋은 풀이를 해내고 싶다.

알고리즘을 잘 푸는 방법은 당연하게도 문제를 많이 풀어보는 것 인데
정답을 보고 코드를 이해하는 것 자체가 공부가 되고, 이후에 정답 안보고 풀기도 하면서
정형화된 유형의 문제들이 익숙해지는 것이 중요하다는 결론을 내렸다.

첫날에는 알고리즘 문제풀이 전략을 살펴보았는데
알고리즘의 정의와 특성, 문제풀이 접근법, 시간복잡도와 공간복잡도에 대해 배웠다.

알고리즘이란 주어진 문제를 해결하기 위한 명확하고 정확한 절차나 규칙의 집합을 의미하며 일련의 단계적인 지시사항이다.
쉽게 말하면 알고리즘은 어떤 문제를 해결하는 방법을 정확하고 단계별로 설명한 것으로 단계별 레시피를 작성하는 것처럼 문제를 컴퓨터에게 해결하도록 지시하는 것이다.

문제를 풀려면 우선 문제를 잘 이해하는데 가장 많은 시간을 들여야 한다.
주어진 문제를 이해하고 요구사항과 예외사항을 파악하고 문제를 더 작고, 더 쉽게 해결하기 쉽게 부분 문제로 나누어 의사코드를 작성할 줄 알아야 한다. 이후에 코드를 구현하면 된다.

문제 풀이 순서
1. 구하는게 무엇인지 파악(문제이해)
2. 주어진게 무엇인지 파악(입력, 제약조건)
3. 무엇을 활용할지(어떤 알고리즘으로 대응할지)
4. 의사 코드를 작성하기
5. 문제를 작은 단위로 나누어서 해결하기(분할 정복)
6. 시간복잡도와 공간복잡도를 고려하기

분할 정복 요령

시작과 끝을 생각하기(입력과 조건)
조금 더 쉬운 버전은? 이것만 해결된다면.. 고민하는 부분이 분할의 지점
출력직전에 어떤 일이 일어났을까?를 생각하기

최악을 가정한 Big-0 표기법
O(1) 스택의 PUSH, POP
O(n) 배열 순회
O(log n) 이진트리
O(n²) 2중 배열 순회, 삽입정렬, 거품정렬, 선택정렬
O(2n) 피보나치

자료구조란
여러 데이터의 묶음을 저장하고 사용하는 방식을 정의해 놓은 것

List와 Array

유효한 인덱스 범위를 벗어나면 IndexOutOfBoundsException이 발생한다.
요소에 순서가 지정된 컬렉션으로 인덱스로 요소에 접근할 수 있다.
파이썬의 경우 리스트에는 다양한 타입을 저장할 수 있지만 배열은 같은 데이터 타입만 저장 가능하다.(자바는 지정된 타입만 가능하다.)
배열이 리스트보다 메모리를 더 효율적으로(적게) 사용한다.

Map

인덱스로 조회할 순 없고, 키를 통해 조회하지만 저장은 순서대로 저장되는 추세이다.
파이썬의 경우 키는 데이터타입이 같고 중복할 수 없지만, 값은 다양한 데이터 타입이 가능하고 중복일 수 있다.(자바는 값도 지정된 타입만 저장가능하다.)

Set

중복을 허용하지 않는 데이터 모임을 다룰 때 효과적이다.

스택

후입선출(LIFO, Last-In-First-Out) 구조
데이터를 가져오는 속도가 빠르지만, 중간요소에 접근이 제한됨
push(파이썬은 append)로 넣고 pop으로 꺼냄
ex) 프링글스, 하노이타워

큐

선입선출(FIFO, First-In-First-Out) 구조
데이터를 순차적으로 처리하고, 삽입과 삭제가 빈번할때 유용함
Insert로 넣고 Remove로 꺼냄
힙을 이용한 우선순위 큐는 우선순위가 높은게 먼저 나옴
ex) 대기표, 빨대

트리

이진트리의 종류 : 정이진트리, 완전이진트리(힙으로 구현가능), 균형이진트리
이진트리에 이진탐색(정렬 후 임의의 수를 찍어서 찾는 값보다 큰지 작은지 확인한 후 반대편을 아예 탐색하지 않는 탐색 알고리즘)을 적용하면 이진탐색트리가 됨
진위순회, 중위순회, 후위순회, 레벨순회방식이 있음
힙(이진트리) < 트리 < 그래프

완전탐색

모든 경우의 수를 탐색하면서 요구조건에 충족되는 결과만 가져오는 알고리즘
DFS(깊이우선), BFS(너비우선)

순열과 조합

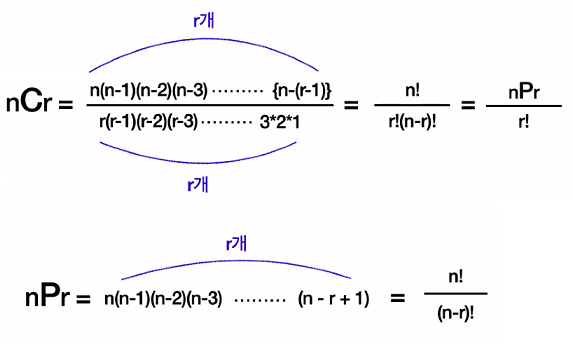
순열(nPr) : n개 중에서 r개를 뽑을때 순서가 있는 조합
조합(nCr) : n개 중에서 r개를 뽑을때 순서없이 조합
중복순열은 요소의 개수보다 뽑는 개수가 클 수 있다.

깊이우선탐색
스택이나 재귀를 이용하여 구현 가능.
문제에서 경로의 특징을 저장해야하거나 노드와 간선이 많은 경우(O(정점*간선)) 사용

시작 정점을 인자로 받는 DFS 함수정의
현재 정점을 방문 처리함
현재 정점과 연결된 인접 정점을 확인
인접 정점 중 방문하지 않은 정점을 재귀적으로 DFS함수에 호출

boolean dfs(int startVertex, int endVertex, int[][] graph) {
    if (startVertex == endVertex) {
        return true; // 시작 정점이 도착 정점과 같으면 경로 찾음
    }

    visited[startVertex] = true; // 현재 정점 방문 처리

    for (int i = 0; i < graph.length; i++) {
        if (graph[startVertex][i] == 1 && !visited[i]) {
            if (dfs(i, endVertex, graph)) {
                return true; // 이어진 길을 찾았으면 true 반환
            }
        }
    }

    return false; // 모든 탐색을 마쳤는데도 도착 정점을 찾지 못함
}

백트래킹 : 더 이상 탐색할 필요가 없다면, 앞선 선택으로 되돌아와 탐색을 반복

너비우선탐색

선형탐색 알고리즘
정렬여부 상관없이 쉽게 구현가능하지만 비효율적이다
시간복잡도 : (O(N)) ex)for문

이진탐색 알고리즘
정렬된 데이터에서 절반씩 범위를 나눠가며 분할정복기법으로 적용하는 알고리즘으로 데이터가 크면 효율적이지만 데이터가 적으면 정렬하는 과정까지 고려하면 효율이 높지 않을 수 있다.
시간복잡도 : (O(logN))

BS(list, num):
	list.sort()
    left = 0
    right = len(list) -1
    
    whlie(left <= right):
    	middle = (right+left) //2
        
        if middle == num;
        	return True;
        elif middle > num;
        	right = middle -1
        else:
        	lift - middle +1
            
    return False

해시탐색 알고리즘
해시 함수를 사용하여 데이터를 검색하는 방법으로 데이터를 고유한 해시 코드(해시 값)으로 변환하고 해시코드를 인덱스를 사용해서 데이터를 해시 테이블에 저장, 검색하는 특징이 있다. 탐색과정이 아닌 해시 함수로 데이터 위치를 알아내므로 값을 찾거나 저장할 때는 해시 함수가 동작하는 만큼의 시간이 소요된다.
단점으로는 데이터의 무결성이 깨지는 경우 해시 충돌이 일어날 수 있다.

시간복잡도: (O(1) + 해싱하는 시간)
ex)룩업테이블을 딕셔너리에 저장해서 활용하는 경우

메모이제이션
동일한 계산을 반복해야 할 때 이전에 계산했던 값들을 메모리에 저장함으로써 동일한 계산의 반복 수행을 제거하여 프로그램 실행 속도를 빠르게 할 수 있는 방법으로 동적 계획법의 핵심이 되는 기술이다.
피보나치를 재귀로 구현하면 f(n) = f(n-1) + f(n-2)인데 f(n-1), f(n-2)에서 각 함수를 1번씩 호출하면 동일한 값을 2번씩 구하게 되어 비효율적이지만 한 번 구한 작은 문제의 결과 값을 저장해두고 재사용하면 O(n^2) → O(f(n)) 로 개선된다.

python
def dp(n):
    if n == 0:
        return 0
    if n == 1:
        fiboList = [0, 1]
        for i in range(2, n + 1):
            num = fiboList[i - 1] + fiboList[i - 2]
            fiboList.append(num)
        return fiboList[n]

java
public static int dp(int n) {
    if (n == 0) {
        return 0;
    }
    if (n == 1) {
        int[] fiboList = {0, 1};
        for (int i = 2; i <= n; i++) {
            int num = fiboList[i - 1] + fiboList[i - 2];
            fiboList = Arrays.copyOf(fiboList, i + 1);
            fiboList[i] = num;
        }
        return fiboList[n];
    }
    return -1; // Handle invalid input
}