
문제
A non-empty array A consisting of N integers is given. Array A represents numbers on a tape.
Any integer P, such that 0 < P < N, splits this tape into two non-empty parts: A[0], A[1], ..., A[P − 1] and A[P], A[P + 1], ..., A[N − 1].
The difference between the two parts is the value of: |(A[0] + A[1] + ... + A[P − 1]) − (A[P] + A[P + 1] + ... + A[N − 1])|
In other words, it is the absolute difference between the sum of the first part and the sum of the second part.
For example, consider array A such that:
A[0] = 3
A[1] = 1
A[2] = 2
A[3] = 4
A[4] = 3
We can split this tape in four places:
P = 1, difference = |3 − 10| = 7
P = 2, difference = |4 − 9| = 5
P = 3, difference = |6 − 7| = 1
P = 4, difference = |10 − 3| = 7
Write a function:
function solution(A);
that, given a non-empty array A of N integers, returns the minimal difference that can be achieved.
For example, given:
A[0] = 3
A[1] = 1
A[2] = 2
A[3] = 4
A[4] = 3
the function should return 1, as explained above.
Write an efficient algorithm for the following assumptions:
N is an integer within the range [2..100,000];
each element of array A is an integer within the range [−1,000..1,000].
문제해석
배열 A를 1부터 N-1까지를 기준으로 나눈 앞의 값들을 더한 모든 값과 뒤의 값들을 더한 모든 값을 뺀 것 중에 가장 작은 값을 찾는 것이다. 그렇다면 배열의 인덱스 1부터 1의 앞의 값과 1부터 마지막까지의 값까지 더한 것을 빼는 과정을 배열의 길이 - 1까지 해야한다. 그리고 뺀 값들 중 가장 작은 값을 찾아서 리턴해주면 된다.
문제풀이
배열을 반복문으로 돌면서 slice와 reduce를 사용해 기준값이 되는 것을 기준으로 두 값을 구하고 뺀 후 가장 작은 값을 찾았다.
틀린 답은 없었지만 효율성에 문제가 발생했고, reduce를 통해 찾는 것을 포기하고 다른 방법을 찾아야했다.
- 기준값의 앞의 값은 0으로 시작하고, 뒤의 값은 배열의 전체합으로 초기화
- 반복문을 돌면서 A[i]를 앞의 값에는 더하고, 뒤의 값에는 뺀다.
- 절댓값을 유지한 채 |앞-뒤| 로 계산해 가장 작은 값을 찾는다.
코드
function solution(A) {
let answer = Infinity;
let left = 0;
let right = A.reduce((a,b) => a+b);
for(let i = 0; i<A.length-1; i++){
left += A[i];
right -= A[i];
answer = Math.min(answer, Math.abs(left-right))
}
return answer
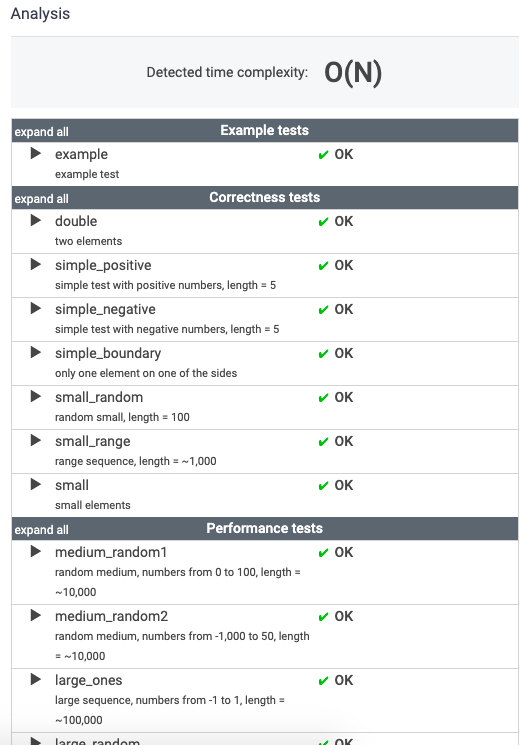
}최종결과
출처
https://app.codility.com/programmers/lessons/3-time_complexity/
