DATA STRUCTURE - 2. (Binary) Tree & BST

트리(Tree)

• 각 노드가 m개 이하의 자식을 가지고 있으면, m-ary 트리(=다항트리, 다진트리)라고 하는데 이때, m=2일 때 즉, 모든 노드의 차수가 2개이하일 때는 특별히 이진트리라고 구분
• 계층적(hierarchical) 관계에 있는 원소들을 나타내기에 편리한 추상 데이터 타입(Abstract Data Type)
• 가장 널리 사용되는 트리 자료구조 : 이진트리, 이진탐색트리(Binary Search Tree)

1. 이진트리의 구조

• 항상 루트노드부터 시작하여 최대 2개의 자식노드를 가짐
• 부모노드와 자식노드는 간선(Edge, Link)로 연결됨
  

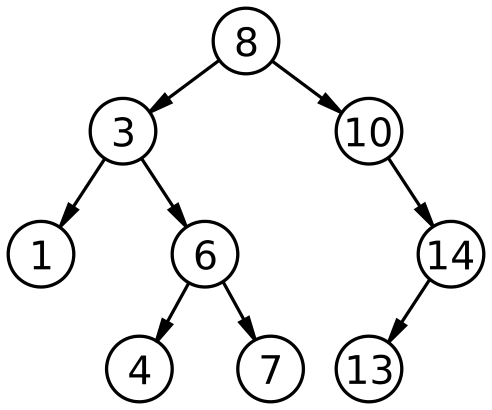
현재 노드가 1 일때 ,

• 트리의 높이(Height) : 루트노드(8) ~ 리프노드 까지의 최대 길이 = 3
• 트리의 깊이(Depth) : 루트노드(8) ~ 현재노드(1)까지의 길이 = 2
• 트리의 차수 : 각 노드의 차수(=자식노드의 개수) 중, 가장 큰 값 = 2

2. 이진트리의 종류

• 정 이진트리(Full Binary Tree) :
  - 모든 노드가 0개 또는 2개의 자식을 가짐
  
  
• 완전 이진트리(Complete Binary Tree) :
  - 마지막 레벨을 제외하고 모든 레벨이 완전히 채워져 있으며, 마지막 레벨의 모든 노드는 가장 왼쪽부터 채워져 있음

       아래 그림은 정 이진트리이자, 완전 이진트리이다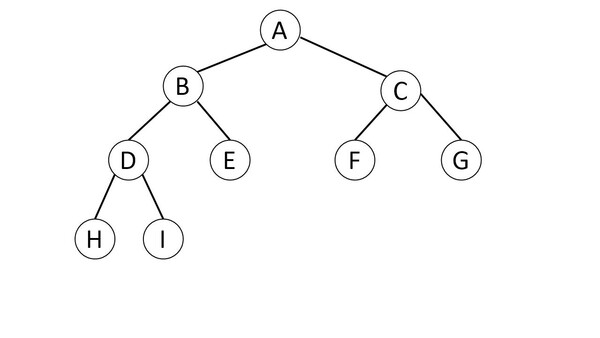

• 포화 이진트리(Perfect Binary Tree) :
  - 모든 노드가 2개의 자식노드를 갖고 있으며 모든 리프노드가 동일한 깊이, 레벨을 가짐.
  
  
  

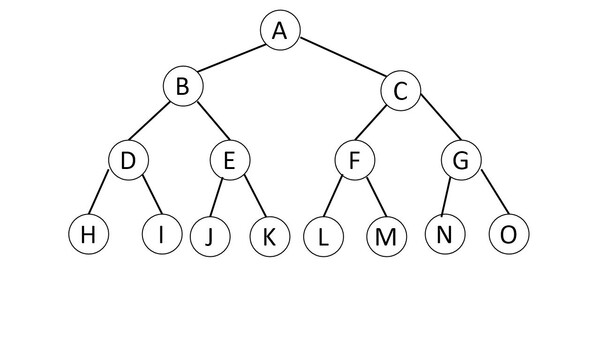
3. 트리의 순회

• 전위순회(Pre-Order) : NLR, 현재노드 - 현재노드의 왼쪽 서브트리 - 현재노드의 오른쪽 서브트리
• 중위순회(In-Order) : LNR, 현재노드의 왼쪽 서브트리 - 현재노드 - 현재노드의 오른쪽 서브트리
• 후외순회(Post-Order) : LRN, 현재노드의 왼쪽 서브트리 - 현재노드의 오른쪽 서브트리 - 현재노드

4. BST(Binary Search Tree)

5. Heap