정렬 왜 해?😐
리스트의 항목을 오름차순 또는 내림차순으로 정렬해 놓으면 리스트에서 어떤 항목을 찾을 때 알고리즘을 이용해서 빠르고 편리하게 찾을 수 있다.
선택 정렬(Selection sort) 알고리즘이란?🤗
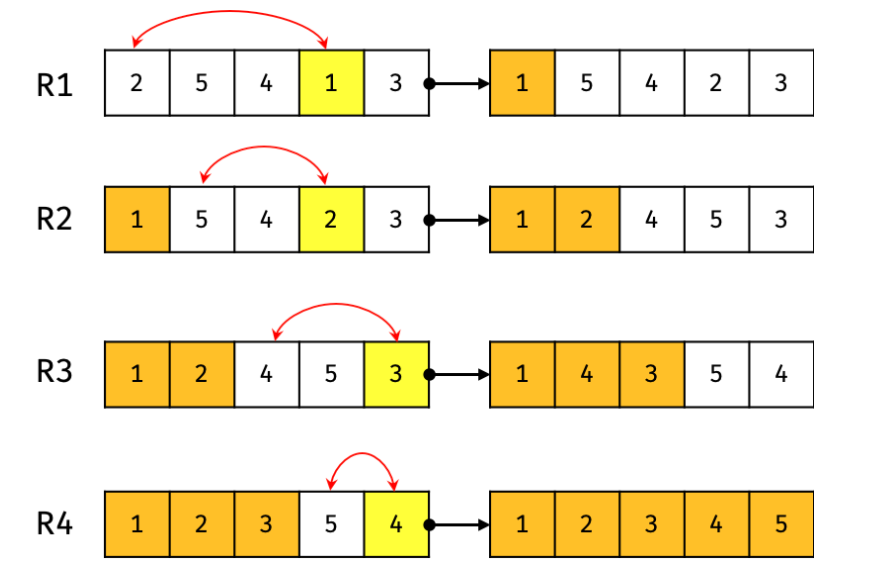
선택 정렬은 선택적으로 값을 교체하는 정렬 방법이다.
- 주어진 리스트 중에 최소값을 찾는다.
- 그 값을 맨 앞에 위치한 값과 교환한다.
- 맨 앞을 제외하고 다시 순회하며 최소값을 찾는다.
- 그 값을 맨 앞 위치 바로 다음 위치와 교체한다. ... 반복
구현
let list = [5, 4, 3, 2, 1];
class SelectionSort {
selection() {
for (let i = 0; i < list.length; i++) {
let minIndex = i;
for (let j = i + 1; j < list.length + 1; j++) {
if (list[j] < list[minIndex]) {
minIndex = j;
}
}
let temp = list[i];
list[i] = list[minIndex];
list[minIndex] = temp;
}
console.log(list);
}
}
const sorter = new SelectionSort();
sorter.selection();버블 정렬(Bubble Sort) 알고리즘이란?🤗
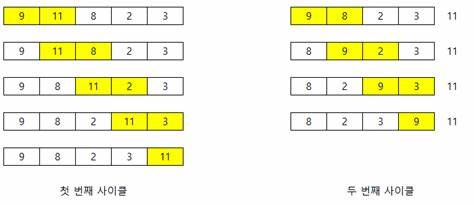
버블 정렬은 요소들이 마치 거품이 일어나듯이 연쇄적으로 자기 자리를 찾아간다고 해서 버블 정렬이란 이름이 붙여졌다.
서로 인접한 두 원소를 검사하여 정렬하는 알고리즘이다.
인접한 2개의 원소를 비교하여 크기가 순서대로 되어 있지 않으면 서로 교환한다.선택 정렬과 기본 개념이 비슷하다.
※ 한 번씩 돌고 끝난 게 아니라 모든 요소를 전부 비교할 때까지 돌아야한다!
(작은 값이 앞에 있는 것을 방지하기 위함)
구현
let list = [5, 4, 3, 2, 1];
let temp = 0;
class BubbleSort {
sort() {
for (let i = 0; i < list.length; i++) {
for (let j = 0; j < list.length - i; j++) {
if (list[j] > list[j + 1]) {
temp = list[j];
list[j] = list[j + 1];
list[j + 1] = temp;
}
}
}
console.log(list);
}
}
const sorter = new BubbleSort();
sorter.sort();
삽입 정렬(Insertion Sort)🤗
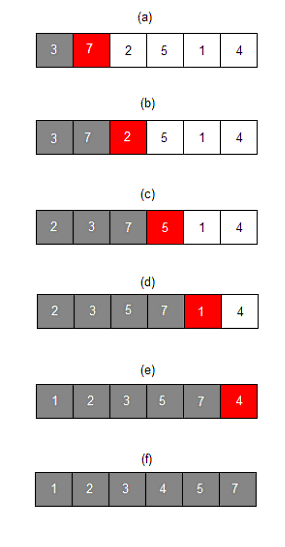
삽입 정렬은 왼쪽에서 오른쪽으로 방향으로 각 요소들을 왼쪽 요소들과 비교하여 알맞은 자리에 삽입하는 형식의 정렬 방법이다. 버블 정렬과 비슷해 보이지만 차이점은 버블은 항상 2개의 요소로 비교를 하고 삽입은 왼쪽에 있는 값들과 비교를 한다는 점이다.
구현
let list = [5, 4, 3, 2, 1];
class InsertionSort {
sort() {
for (let i = 1; i < list.length; i++) {
let currentElement = list[i];
let j = i - 1;
while (j >= 0 && list[j] > currentElement) {
list[j + 1] = list[j];
j--;
}
list[j + 1] = currentElement;
}
console.log(list);
}
}
const sorter = new InsertionSort();
sorter.sort();트리 정렬(Tree Sort)이란?😀
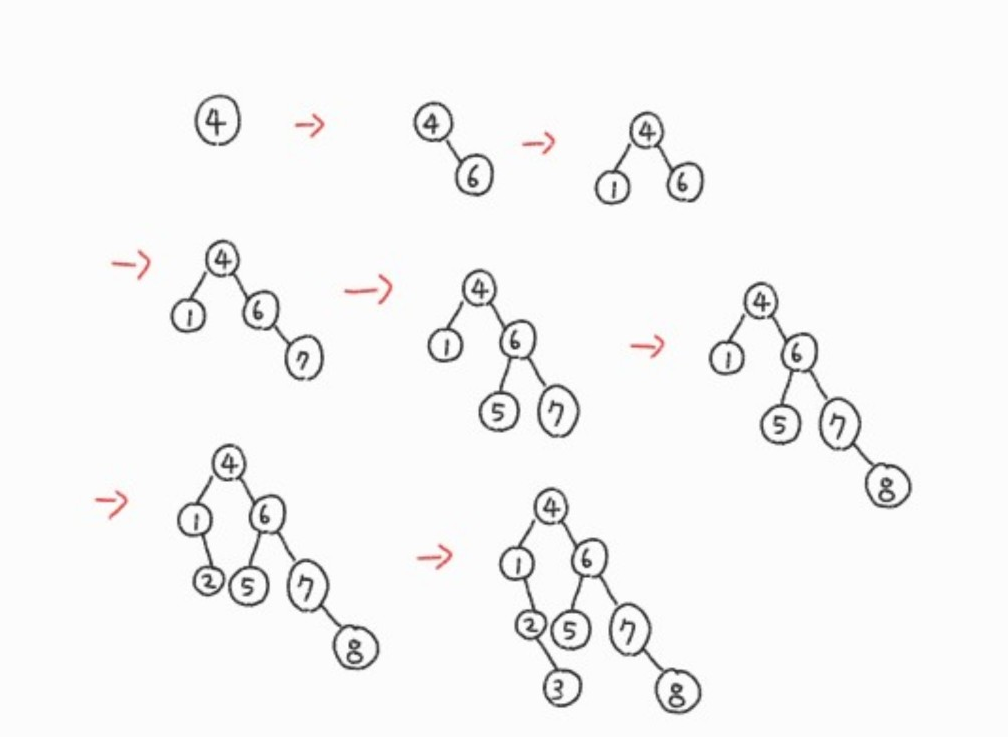
이진 탐색 트리를 만들어 정렬하는 방식이다. [4, 6, 1, 7, 5, 8, 2, 3]을 다음과 같은 과정을 통해 트리 정렬을 수행할 수 있다.
-
이진 탐색 트리 생성
부모노드보다 큰 노드는 오른쪽으로, 작은 노드는 왼쪽에 간다.
-
중위순회
왼쪽 하위 트리를 방문 후 뿌리(root)를 방문하는 순회 방식인데, 참고로 이때의 뿌리는 4를 뜻한다.
따라서 1, 2, 3, 4, 5, 6, 7, 8로 정렬된다. -
구현
class TreeNode { constructor(value) { this.value = value; this.left = null; this.right = null; } } //트리 값 추가 function insert(root, key) { if (root === null) { return new TreeNode(key); } if (key < root.value) { root.left = insert(root.left, key); } else if (key > root.value) { root.right = insert(root.right, key); } return root; } //중위 순회 function inOrderTraversal(root, result) { if (root !== null) { inOrderTraversal(root.left, result); result.push(root.value); inOrderTraversal(root.right, result); } } function treeSort(arr) { let root = null; for (let i = 0; i < arr.length; i++) { root = insert(root, arr[i]); } let result = []; inOrderTraversal(root, result); return result; } const inputArray = [4, 6, 1, 7, 5, 8, 2, 3]; console.log(treeSort(inputArray));
병합 정렬(Merge Sort)이란?😊
주어진 배열을 원소가 하나 밖에 남지 않을 때까지 계속 둘로 쪼갠 후에 다시 크기 순으로 재배열 하면서 원래 크기의 배열로 합칩니다. [6, 5, 3, 1, 8, 7, 2, 4]를 다음과 같은 과정을 통해 병합 정렬할 수 있다.
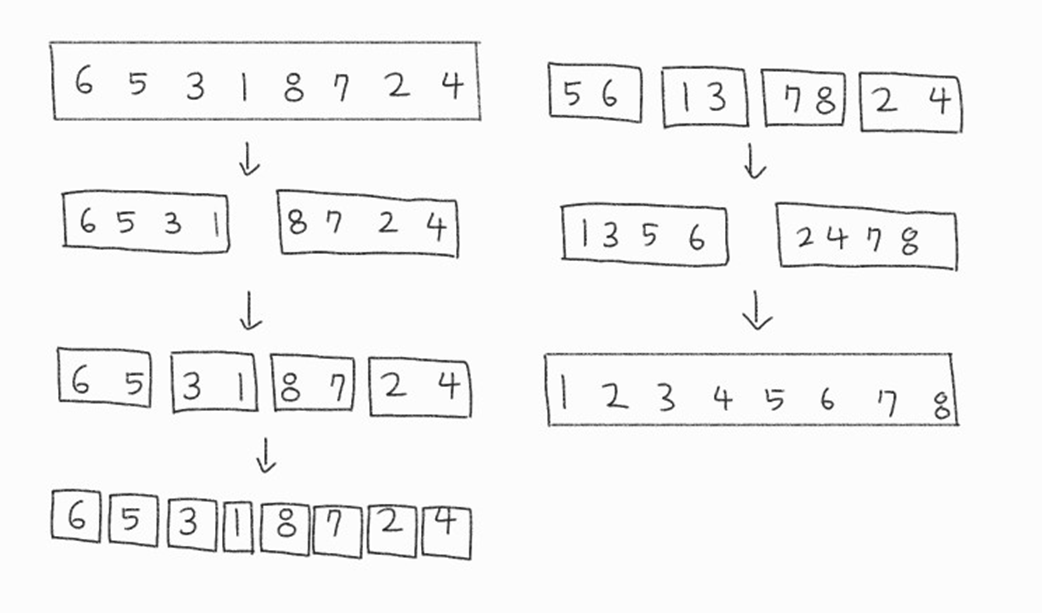
-
구현
function mergeSort(arr) { if (arr.length <= 1) { return arr; } const middle = Math.floor(arr.length / 2); const left = arr.slice(0, middle); const right = arr.slice(middle); return merge(mergeSort(left), mergeSort(right)); } function merge(left, right) { let result = []; let leftIndex = 0; let rightIndex = 0; while (leftIndex < left.length && rightIndex < right.length) { if (left[leftIndex] < right[rightIndex]) { result.push(left[leftIndex]); leftIndex++; } else { result.push(right[rightIndex]); rightIndex++; } } return result.concat(left.slice(leftIndex)).concat(right.slice(rightIndex)); } const inputArray = [6, 5, 3, 1, 8, 7, 2, 4]; console.log(mergeSort(inputArray));
