 현미경과 계산기를 갖춘 휴먼 컴퓨터, 1952
현미경과 계산기를 갖춘 휴먼 컴퓨터, 1952
컴퓨터의 개념
A computer is a machine that can be programmed to carry out sequences of arithmetic or logical operations (computation) automatically.
컴퓨터는 일련의 산술연산 또는 논리연산을 자동으로 수행하도록 프로그래밍 할 수 있는 기계이다.
-wikipedia
애초에 컴퓨터는 계산하다라는 라틴어 '콤푸타레'(computare)를 어원으로 한다.
컴퓨터의 기능
- 입력
프로그램을 컴퓨터 내부의 메모리로 읽어들이는 입력 장치의 기능이다. - 제어
프로그램의 명령을 하나씩 읽고 해석하여, 모든 장치의 동작을 지시하고 감독·통제하는 기능이다. (CPU가 담당) - 기억 및 저장
입력 장치로 읽어들인 데이터나 프로그램, 중간 결과 및 처리된 결과를 기억하는 기능으로서 중앙 처리 장치의 주기억 장치와 보조 기억 장치에 갖추어져 있다.(주기억장치: HDD, SSD 보조 기억 장치: RAM) - 연산
기억된 프로그램이나 데이터를 꺼내어 산술이나 논리셈따위를 하는 기능 (CPU담당) - 출력
프로그램의 결과를 빛, 화면, 소리, 잉크 등의 수단으로 출력하는 장치의 기능이다. (모니터 프린터 등)
컴퓨터의 역사
컴퓨터가 개발되기 이전
기존의 인간들은 막대기를 나열하거나 손가락으로 수를 세는 방법으로 계산에 도움을 받았다. 이를 조금 더 발전된 방식으로 주판과 같은 도구들이 나오기도 하였다.
최초의 기계식 컴퓨터
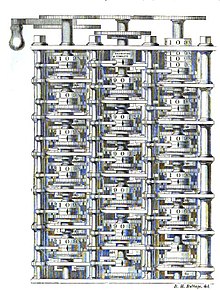

최초의 컴퓨터는 '영국의 기계공학자 Charles Babbage'에 의해 발명된 Babbage's Difference engine이다. 이는 기계식으로서 기어를 활용하여 연산을 처리한다.
전자식 컴퓨터
처음 전자식 컴퓨터는 Electromechanics에 의해 구현되기 시작했다. Electromechanics은 전기 공학과 기계 공학의 프로세스가 결합된 형태이다. 엄밀히 말하자면 스위치를 예시로 (기계적으로 버튼을 누르는 과정 + 전기적 신호) 들 수 있다.
애니악의 알고리즘을 직접 갈아끼우고 있는 모습 이를 하드와이어링 방식이라고 한다
이러던 와중 진공관(Vacuum tube)의 발명으로 기존의 Electromechanics을 전자식으로 바꿔놓았고, 디지털 계산이 아날로그를 대체하게 된다. ex)전화 교환원을 진공관이 대체하는 것
그러나 이 시대의 대표적인 컴퓨터 '애니악'도 아직까지는 알고리즘 스위치를 사람이 직접골라 연결하는 방식이였다. 원하는 연산에 맞는 선을 연결해줘서 알고리즘을 변경한 것이다. (이는 한 기계당 한 가지 문제 해결능력을 가졌다는 것을 의미한다.)
현대의 컴퓨터
엘런 튜링의 튜링머신이론

현대의 컴퓨터는 엘런 튜링의 '튜링머신이론'을 기반으로 하고있다. (튜링은 튜링테스트를 만든 사람이기도 하다.)
튜링머신의 역사
튜링머신은 사실 힐베르트의 결정문제를 해결하기 위해 엘런튜링이 고안한 가상의 기계이다.
힐베르트의 결정문제는 제안한 20세기에 해결해야할 23가지 문제들 중 10번째 문제이다.
"Find an algorithm to determine whether a given polynomial Diophantine equation with integer coefficients has an integer solution."
(정수 계수를 갖는 주어진 다항식 디오판틴 방정식이 정수 해를 갖는지 여부를 결정하는 알고리즘을 찾아라.) 이는 디오판틴 방정식의 특성 때문에 수학자들에 의하면 "많은(또는 심지어 모든) 수학적 명제의 해결하는 알고리즘을 구하라." 라는 의미로 해석된다.
이를 위해 계산할 수 있는 모든 수학적 명제를 해결하는 튜링머신을 개발하게 된다.
튜링머신의 구조
튜링머신 튜링머신은 0과 1로 이루어진 끝없이 이어지는 테이프(input), 값을 읽어주는 스캐너, 스캐너가 값을 읽는 규칙으로 구성되어 있다.

스캐너는 값을 읽어가며 특정 규칙에 맞춰 테이프의 값을 바꿔준다(값을 읽고 -> 특정규칙에 맞춰 -> 값을 변화하거나 그대로 두고(if) -> 이동한다 (이때이 규칙은 특정 상태와 읽은 값을 조건으로 움직이는 방향(또는 안움직일지), 변화할 상태, 읽은 값을 어떻게 바꿀지에 대해 적혀있다.).
즉 이부분은 알고리즘에 해당하며 추후 완성된 테이프는 결과(output)가 된다. 그러나 이렇게 끝나면 한가지 특정규칙(알고리즘)만을 수행해주는 일반적인 기계이다.
만능튜링머신
이렇게 나온것이 만능튜링머신이다. 아까의 특정 규칙을 0과 1로 변환한다. 그렇다면 알고리즘에 해당하는 특정규칙을 테이프의 input 앞 head에 넣고 돌려준다. 그리고 이를 읽어주는 스캐너에 알고리즘 해석방법을 규칙으로 넣어준다. 이렇게 만들어진 것이 만능튜링머신이다. 이 오토마타의 대단한 점은 하나의 기계가 특정 계산이 아닌 모든 계산을 수행할 수 있다는 점이다.
여기서 컴퓨터가 튜링머신과 같이 모든 계산이 가능한가에 따라 Turing completeness(튜링 완전성) 이라는 새로운 분류 기준이 되기도 하였다. (특정계산만 하는 컴퓨터 vs 모든계산이 가능한 튜링 완전성을 가진 컴퓨터)
만능튜링머신의 의의
현재 컴퓨터는 튜링머신이론을 기반으로 만들어졌다. 때문에 튜링머신과 같이 모든 연산을 할 수 있고, 튜링머신의 한계점 또한 함께 공유한다는 점에서 굉장히 중요한 이론이다. 아까 말했듯 튜링머신은 계산 가능한 수학적 명제에 대해 만능이기에 '계산'이라는 정의를 판단하거나 어떤 알고리즘으로 문제가 해결될때 걸리는 시간의 결정에서도 의미가 깊다.(계산이론 - 계산가능성, 계산복잡도)
정지문제
이제 다시 힐베르트의 결정 문제로 돌아가보자. 엘런튜링은 "많은(또는 심지어 모든) 수학적 명제의 해결하는 알고리즘을 구하라." 라는 문제를 튜링머신을 활용하여 정지문제(Halting problem)로 바꿨다.
https://www.youtube.com/watch?v=92WHN-pAFCs
(정지문제를 소개하는 유튜브 영상)
프로그램을 설명한 것과 처음 입력값이 주어졌을 때, 이 프로그램에 입력값을 넣고 실행한다면 이 프로그램이 계산을 끝내고 멈출지 아니면 영원히 계속 계산할지 판정하라.
프로그램 H에 대해서 생각해보자, H에 프로그램a를 설명한 것과 input(0)을 넣으면 H는 프로그램a에 input(0)가 들어가면 시뮬레이션하여 프로그램a가 멈출지 계속 작동할지 판단하여 알려준다.
프로그램 N에 대해서 생각해보자, N은 H가 준 멈출지 계속 작동할지에 대한 판단을 입력받아 반대로 출력한다.
이렇게 해서 H와 N프로그램을 엮는다. 이를 HN프로그램이라고 하자.
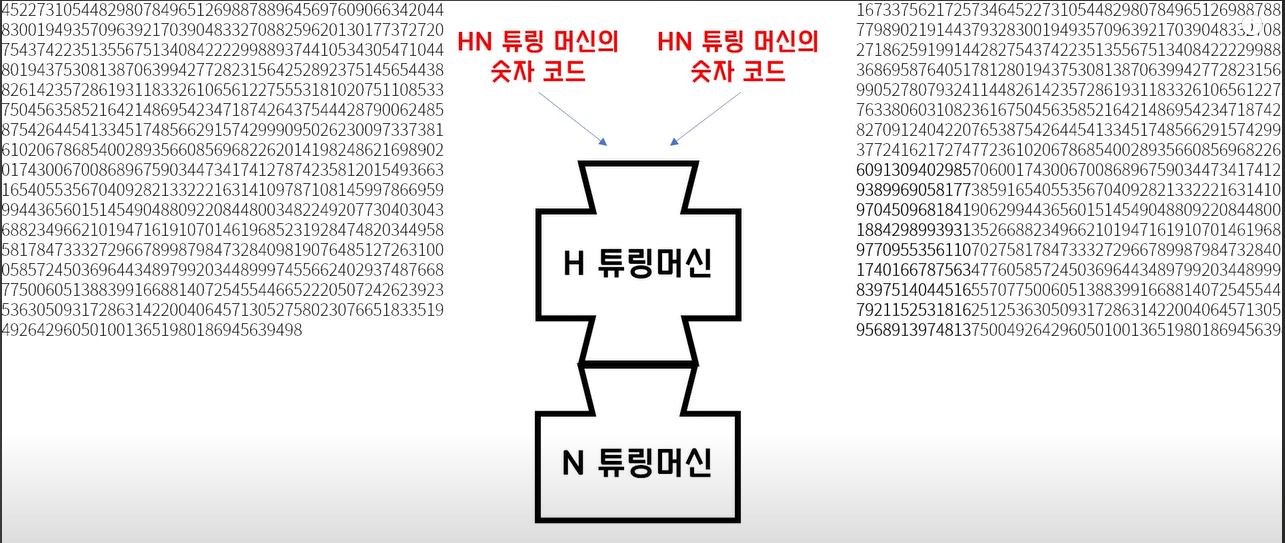
이번엔 HN프로그램에 두 입력값에 모두 HN프로그램을 넣는다.(프로그램은 실제로 코드이며 튜링머신에서도 알고리즘을 테이프에 기록했다는 점을 보면 당연히 가능하다.)
이떄 HN프로그램은 무슨 결과를 내던 모순을 일으킨다.
(정상작동한다 -> H에서는 HN이 멈춘다고 판단한 것인데 -> 정상작동했다.)
(멈춘다 -> H에서는 HN은 정상작동한다고 판단한 것인데 -> 멈췄다.)
즉 어떤 프로그램이 계산을 끝내고 멈출지 정상작동할지 판단하는 프로그램은 존재할 수 없다. -> 모든 수학적 명제를 해결하는 프로그램은 존재할 수 없다.
이는 튜링머신(또는 현대의 컴퓨터)가 모든 수학적 명제가 아닌 계산 가능한 명제만을 해결할 수 있다는 것을 의미하며, 동시에 어떤 명제가 계산 가능한가에 대한 판단 기준이 된다. 또한 이는 처음으로 증명된 정의되지 않는 결정문제이다.
튜링머신의 의의 재정리
- 모든 알고리즘을 다룰 수 있는 현대의 컴퓨터의 기반이 됌 (한계를 정의하거나 계산 능력을 평가함에 있어 튜링완전한 기계들은 모두 동일)
- 계산 가능한 명제에 대한 판단 기준으로서, 튜링머신으로 해결 가능한가에 따라 구분할 수 있다.(계산 가능한 명제라는 것은 모두 튜링머신으로 해결가능)
- 수학적으로 처음 증명된 undecidable(결정불가) 결정문제(Entscheidungsproblem)였다.
튜링머신은 한 기계에서 모든 알고리즘을 프로그래밍하고 사용할 수 있었기에 직접 함수에 배선을 연결해서 쓰던 구조를 대신하게 되었다.
엘런튜링 파트 참고자료
[정지문제]https://www.youtube.com/watch?v=92WHN-pAFCs
[튜링 머신과 최초의 컴퓨터 (튜링 머신 #1~#4)]https://www.youtube.com/watch?v=THocNNqgqeQ
[Turing machine - wikipedia]https://en.wikipedia.org/wiki/Turing_machine#cite_note-13

