컴퓨터가 발전하면서 어떤 문제를 알고리즘으로 해결하는 과정에서 문제들이 알고리즘으로 빠른시간에 해결되기도 하는 반면 매우 오래걸리는 문제들도 있었다. 때문에 이를 계산복잡도에 나누기 시작했고, p문제 np문제가 수학적으로 정의되었다.
P 문제, NP 문제
P 문제: 결정론적 튜링머신에 의해 다항시간안에 계산이 가능한 문제
NP 문제: 비결정론적 튜링머신에 의해 다항시간안에 계산이 가능한 문제
여기서 다항시간이란 빅오 자료형으로 표현하면 O(N^2)와 같은 시간복잡도를 의미하며, NP의 경우 O(N!) O(2^N)과 같은 시간복잡도를 가진다. 또한 NP를 다른 말로 표현하자면 검산은 다항시간안에 결정론적 튜링머신에 의해 가능한 문제(쉬운)이다.
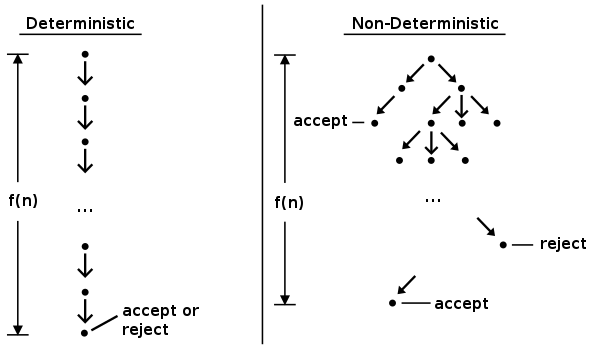
결정론적 튜링머신과 비결정론적 튜링머신은 튜링머신에 대한 이해가 필요한다. 위 그림은 시간에 따른 결정론적 튜링머신의 탐색과 비결정론적 튜링머신의 탐색을 비교한 것이다. 기본적인 튜링머신의 경우 헤드가 1번에 1개의 상태를 가지는 결정론적 튜링머신의 형태이다. 그러나 비결정론적 튜링머신은 상태를 변경할때 0~N개의 다양한 상태를 지시하며, 이는 트리구조의 그래프를 level별로 한번에 탐색하는 것과 비슷한 효과를 낸다.(여러개의 결정론적 튜링머신이 한번에 연산하는 효과)
P NP 문제
컴퓨터의 성능의 발전속도는 빠르기 때문에 P문제(ex 곱하기연산, 정렬 알고리즘)들은 기다리면 쉽게 해결되리라 예상했지만 NP(ex 스도쿠)의 경우 복잡도가 데이터에 따라 너무 커져 이는 충분히 문제가 되었다. 시간이 지남에 따라 NP문제들 중 다행히 P문제라고 밝혀진 문제들이 있었지만, 많은 문제들이 여전히 NP문제로 남아있었고 이 중에는 사회적으로 매우 중요한 문제들도 있었다. 그래서 사람들이 P = NP문제인데 아직 좋은 알고리즘을 못 찾은건지, 아니면 진정으로 어려운 NP라는 문제가 실제로 존재하는지 의구심을 품었고 이것을 P NP문제라고 부른다.

위 그림은 P NP문제의 결론에 따른 구조를 그래프로 시각화 한 것이다. 아래에는 이 그림에서 처음 배우는 내용을 적겠다.
- P문제는 결정론적 튜링머신으로 다항시간안에 풀 수 있는 문제기에 당연히 비결정론적 튜링머신으로도 다항시간 안에 풀 수 있다. 즉 P문제는 기본적으로 NP문제의 부분집합이다.
- NP-Hard : np문제에 속하는 모든 판정문제를 다항시간 안에 N:1관계로 환산되는 문제들을 의미한다. 난이도는 당연히 최소 NP이상이다.(계산복잡도 이론에서의 환산은 어떤 문제를 다른 문제로 변형하는 과정을 의미한다.)(NP-hard문제들에는 정의조차 되지 않은 문제도 있다.)
- NP-Complete : NP와 NP-Hard의 교집합이다. (조건을 정리하자면 NP문제이며, 다른 모든 NP문제로부터 다항시간 안에 N:1관계로 환산된다.) (ex 외판원 문제)
그래프를 이해하기 전 NP-Complete가 가지는 중요성에 대해 이해할 필요가 있다. 사람들은 NP문제들을 환산해보던 도중 NP문제가 사실 핵심적으로 같은 부분에서 NP문제 였음을 깨달았는데. 이 코어와 같은 역할을 하는 것이 NP-Complete이다. 만약 NP-complete 문제 중 하나라도 P 문제라고 판명나는 순간 P=NP임을 알 수 있는 것이다. (재미있는 예로 스도쿠를 빨리 푸는 법을 깨달으면 단백질 접힘 계산과 정확히 동일한 NP문제를 해결한 것인데, 이는 암 치료에 도움이 된다.)
이제 그래프를 이해할 수 있다.
- P != NP의 경우 당연히 NP-Complete와 P는 전혀 다른 집합이며 둘 모두 NP의 부분집합이다.
- P = NP의 경우 P = NP = NP-Complete로 모든 문제를 결정론적 튜링머신으로 다항시간안에 풀 수 있다.
현대 사람들은 83%가 NP != P 라고 생각한다고 한다. (전문가만 하면 90%를 넘는다고 한다) 그런데 왜 이걸 증명 못하는 걸까? 재미있게도 P NP문제 증명 자체가 NP문제이기 때문에 그렇다고 한다.