그래프 탐색(그래프 순회) 알고리즘

Solf·2022년 9월 4일

알고리즘 이론

목록 보기

8/14

탐색: 많은 양의 데이터 중에서 원하는 데이터를 찾는 과정
대표적 예시 - DFS/BFS 코테에 자주 등장함.

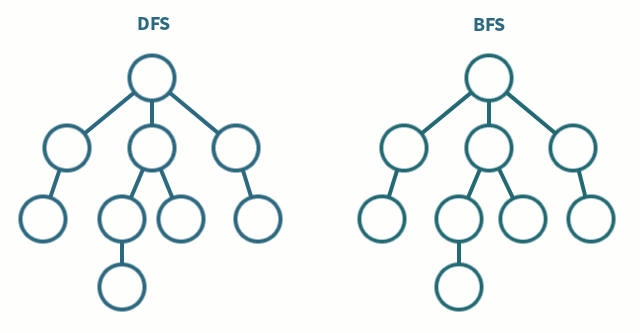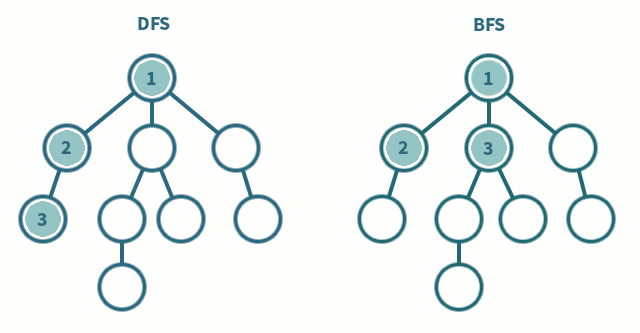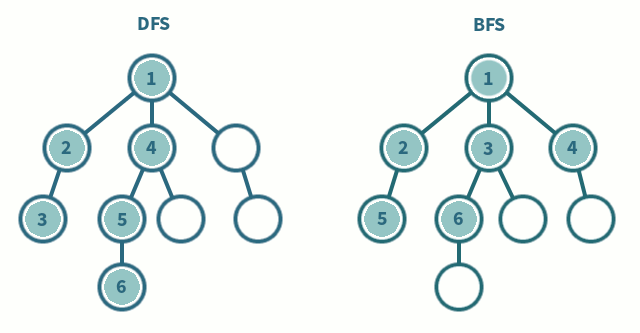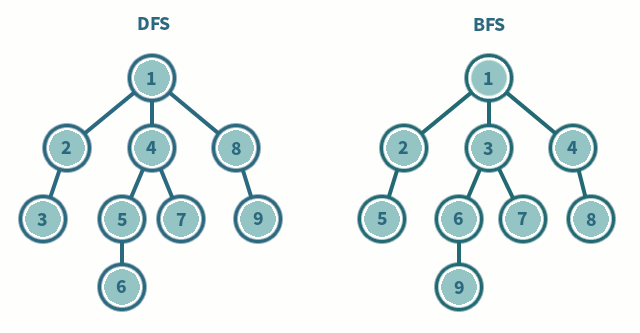
깊이 우선 탐색(DFS, Depth-First Search)

그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘.
구현시 스택자료구조(혹은 재귀 함수)를 이용

알고리즘
1. 탐색 시작 노드를 스택에 삽입하고 방문 처리
2. 스택의 최상단 노드에 방문하지 않은 인접한 노드가 하나라도 있으면 그 노드를 스택에 넣고 방문 처리, 방문하지 않은 인접 노드가 없으면 스택에서 최상단 노드를 호출
3. 더 이상 2번의 과정을 수행하지 못할 때까지 반복

컴퓨터가 함수를 연속적으로 호출하면 컴퓨터 메모리 내부에 스택 프레임이 쌓임.
따라서 스택을 사용해야 할 때 구현상 스택 라이브러리 대신 재귀함수를 대신 이용하는 경우가 많

장점

현 경로상의 노드를 기억하기 때문에 적은 메모리를 사용
찾으려는 노드가 깊은 단계에 있는 경우 BFS보다 빠름

단점

해가 없는 경로를 탐색할 경우 단계가 끝날 때까지 탐색. 효율성을 높이려면 임의의 깊이를 지정해 탐색하고 해가 없다면 빠져나와 다른 경로로 가는 알고리즘을 추천
DFS를 통해서 얻어진 해가 무조건 최단 경로는 아님. DFS는 해에 도착하면 탐색을 종료하기 때문.

파이썬 구현

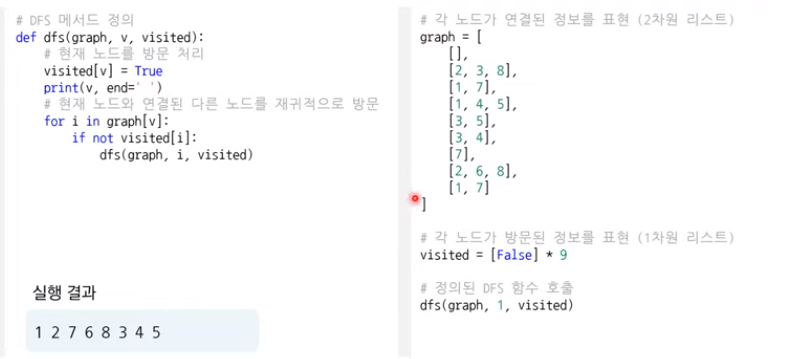
너비 우선 탐색(BFS,Breadth-First Search)

그래프에서 가까운 노드부터 우선적으로 탐색하는 알고리즘.
구현시 큐 자료구조를 이용(재귀로는 구현 불가능)

알고리즘
1. 탐색 시작 노드를 큐에 삽입하고 방문 처리
2. 큐에서 노드를 꺼낸 뒤 해당 노드의 인접 노드 중에서 방문하지 않은 노드를 모두 큐에 삽입하고 방문 처리
3. 더 이상 2번의 과정을 수행하지 못할 때까지 반복

장점

답이 되는 경로가 여러개 여도 최단경로임을 보장
최단 경로가 존재하면 깊이가 무한정 깊어진다고 해도 답을 찾을 수 있음

단점

경로가 매우 길 경우에는 탐색 가지가 급격히 증가함에 따라 보다 많은 메모리 필요
해가 존재하지 않는다면 유한 그래프의 경우에는 모든 그래프를 탐색하고 실패로 끝남
무한 그래프의 경우에는 결코 해를 못 찾고, 끝내지도 못함

파이썬 구현

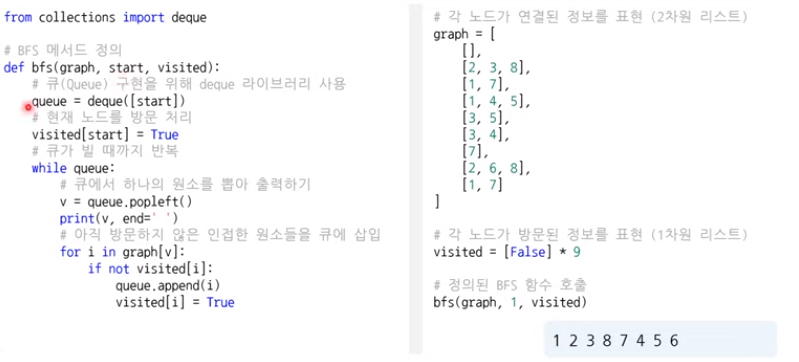
DFS, BFS 비교분석

시간복잡도: 모두 조건내의 모든 노드를 분석하기에 시간복잡도는 동일

단. 적합한 문제 유형이 있음

그래프의 모든 정점을 방문하는 것이 주요한 문제: 상관 없음
경로의 특징을 저장해둬야 하는 문제: DFS가 유리 - ex) 백트래킹 - 정점에 숫자가 있어 a부터 b까지 가는 경로를 구하는데 경로에 같은 숫자가 있으면 안된다는 조건! BFS는 경로의 특징을 가지지 못함
최단거리 구하는 문제: BFS가 유리 경로 탐색중 가장 먼저 도달하는 루트가 최단거리.

이 외엔

검색 대상 그래프가 크다: DFS 우선
검색 대상 규모가 크지 않고, 검색 시작 지점으로부터 원하는 대상이 별로 멀지 않다: BFS 우선

상태공간 트리(State-Space Tree)

문제해결과정의 중간 과정을 노드로 leaf node에 해를 두는 트리이다.

back tracking

그래프를 탐색하다가 안되면 되돌아가는 방식
주의할 점은 백트래킹은 dfs에 종속되는 것이 아니다. 상태공간 트리를 탐색하는 방법으로서도 백트래킹이라는 표현을 쓴다.

branch and bound

그래프 노드에서 가능성이 있는 노드만 뻣어나가는 방식
dfs의 백트래킹의 bfs 버전이라고 보면 쉽다. 동일하게 상태공간 트리를 탐색하는 방법으로서 사용하는 표현이니 bfs에 종속하지 말것.

주의

back tracking과 branch and bound 방식은 DFS와 BFS의 기법이라기보다 별개의 알고리즘으로 봐주는게 맞다고 한다.

그래프에서는 DFS와 BFS, 트리에서는 back tracking와 branch and bound라는 표현을 사용.

BFS/DFS 코테

코테에서 적용할만한 팁들을 정리해보겠다.

DFS는 재귀로 구현할 시 스택오버플로우가 발생할 가능성이 있어 반복문으로 구현하는게 좋다.
반복문으로 보면 DFS/BFS는 정말 거의 동일한 코드를 가진다.

#### 그래프 정보 및 공통 부분 ####

# 방문 정보를 리스트 자료형으로 표현
visited =[False] * 9

# 각 노드가 연결된  정보를 리스트 자료형으로 표현 (2차원 리스트)
graph = [
  [],                 # 1번 노드와 연결된 노드들
  [2, 3, 8],          # 2번 노드와 연결된 노드들
  [1, 7],             # 3번 노드와 연결된 노드들
  [1, 4, 5],          # 4번 노드와 연결된 노드들
  [3, 5],             # 5번 노드와 연결된 노드들
  [3, 4],             # 6번 노드와 연결된 노드들
  [7],                # 7번 노드와 연결된 노드들
  [2, 6, 8],          # 8번 노드와 연결된 노드들
  [1, 7]              # 9번 노드와 연결된 노드들
]

#### DFS ####
def DFS(graph, start, visited):
  stack = [v]

while stack:
   v = stack.pop()
   print(v, end = ' ')
   visited[v] = True # 방문처리를 외부에서 함

  for i in graph[v]:
    if not visited[i]:
    	stack.append(i)
      
 DFS(graph, 1, visited)


#### BFS ####
from collections import deque

def BFS(graph, start, visited):
  queue = deque([start])
  visited[start] = True # 첫번째 방문처리만 메인 반복문 밖에서

  while queue:
    v = queue.popleft()
    print(v, end = ' ')

    for i in graph[v]:
      if not visited[i]:
        queue.append(i)
        visited[i] = True # 방문처리를 내부에서 함

BFS(graph, 1, visited)

# https://daekyoulibrary.tistory.com/entry/Python-%ED%8C%8C%EC%9D%B4%EC%8D%AC%EC%9D%84-%ED%86%B5%ED%95%B4-%EA%B5%AC%ED%98%84%ED%95%9C-DFS%EC%99%80-BFS