최단경로 문제

Solf·2022년 9월 13일

알고리즘 이론

목록 보기

11/14

https://yganalyst.github.io/concept/algo_cc_book_7/

최단경로 문제는 노드와 간선이 있을 때 말 그대로 특정 노드간 최단경로를 구하는 것을 의미한다. (다이나믹 프로그래밍으로 분류되기도 함)

다익스트라 최단 경로 알고리즘

다익스트라가 제안한 알고리즘 중 하나로, 특정한 노드에서 출발해 다른 모든 노드로 가는 최단 경로 계산 (그리디 알고리즘으로 분류)

조건

음의 간선이 없을 때 정상작동 (현실세계의 도로(간선)은 음의 간선으로 표현 X)

알고리즘

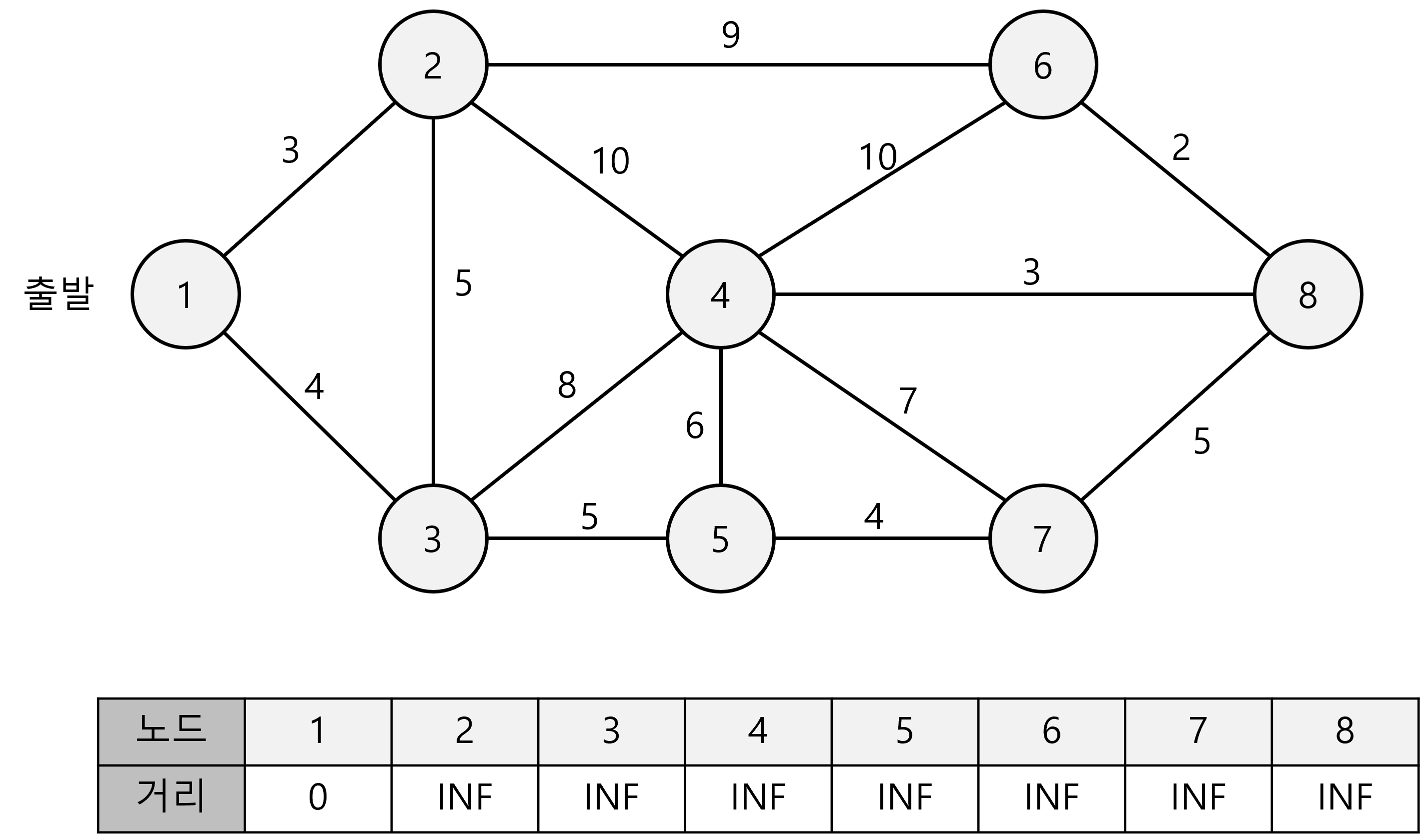
출발 노드를 설정
최단 거리 테이블을 초기화 (본인: 0 나머지 노드: INF(무한))
방문하지 않은 노드 중에서 최단거리가 가장 짧은 노드를 선택 (그리디)
해당 노드를 거쳐 다른 노드로 가는 비용을 계산하여 최단 거리 테이블을 갱신
3번과 4번 과정 반복

필요한 메모리

특정 노드로부터 다른 노드까지의 최단거리를 갱신하며 저장할 1차원 배열
현재 이동할 수 있는 노드 중 갈 수 있는 가장 짧은 노드를 뽑을 우선순위큐(최소 힙)

위에서 방문처리에 대한 이야기를 했는데 이는 조건문을 통해 간략화한다.

시간복잡도

V개의 노드를 탐색하며 가장 짧은 노드를 항상 V길이의 배열을 탐색 : O(V^2)

but. E간선을 탐색하며 최소힙을 사용하면 힙 삽입 삭제가 O(log E): O(E log E)
이때 중복간선이 없다면 E < V^2 을 만족하므로 log E < 2 log V, 즉 O(E log V)로 봐도 된다.

코드

비교적 빠른 최소힙을 활용한 코드를 보자

import heapq  # 우선순위 큐 구현을 위함

def dijkstra(graph, start):
  distances = {node: float('inf') for node in graph}  # start로 부터의 거리 값을 저장하기 위함
  distances[start] = 0  # 시작 값은 0이어야 함
  queue = []
  heapq.heappush(queue, [distances[start], start])  # 시작 노드부터 탐색 시작 하기 위함.

  while queue:  # queue에 남아 있는 노드가 없으면 끝
    current_distance, current_destination = heapq.heappop(queue)  # 탐색 할 노드, 거리를 가져옴.

    if distances[current_destination] < current_distance:  # 기존에 있는 거리보다 길다면, 볼 필요도 없음(방문처리역할)
      continue
    
    for new_destination, new_distance in graph[current_destination].items():
      distance = current_distance + new_distance  # 해당 노드를 거쳐 갈 때 거리
      if distance < distances[new_destination]:  # 알고 있는 거리 보다 작으면 갱신
        distances[new_destination] = distance
        heapq.heappush(queue, [distance, new_destination])  # 다음 인접 거리를 계산 하기 위해 큐에 삽입
    
  return distances
  
  graph = {
    'A': {'B': 8, 'C': 1, 'D': 2},
    'B': {},
    'C': {'B': 5, 'D': 2},
    'D': {'E': 3, 'F': 5},
    'E': {'F': 1},
    'F': {'A': 5}
}

print(dijkstra(graph, 'A'))

#{'A': 0, 'B': 6, 'C': 1, 'D': 2, 'E': 5, 'F': 6}
#https://justkode.kr/algorithm/python-dijkstra/