Graph
1. 개념
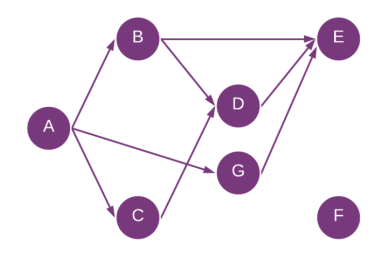
- 컴퓨터 공학에서의 그래프 : 네트워크 망 형태
- 여러개의 점들이 서로 복잡하게 연결되어 있는 구조
- 정점(vertex) : 그래프 상의 점
- 간선(edge) : 하나의 선
- 직접적인 관계가 있는 경우 두 점 사이를 이어주는 선이 존재
- 인접 매트릭스 또는 인접 리스트로 표현 가능
2. 그래프의 표현 방식
- 인접 행렬 : A라는 정점과 B라는 정점이 이어져 있다면 1(true), 이어져 있지 않다면 0(false)으로 표시한 일종의 표
*가장 빠른 경로(shortest path)를 찾고자 할 때 주로 사용 - 인접 리스트 : 각 정점이 어떤 정점과 인접한지를 리스트의 형태로 표현
*정점마다 하나의 리스트를 가지고 있으며, 이 리스트는 자신과 인접한 다른 정점을 담고 있음
1) 인접 매트릭스(adjacency matrix)
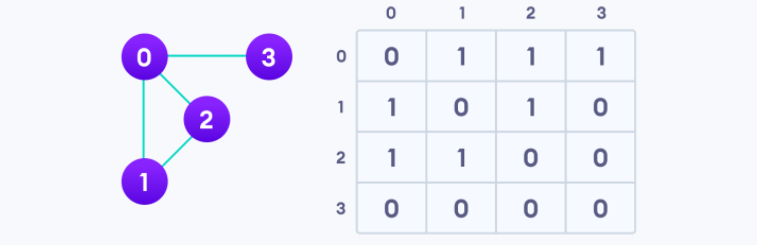
- 세로 : from & 가로 : to의 2차원 배열
- 각 vertex가 연결되어 있으면 [from][to] = 1
*edge가 있음을 의미 - edge 삭제 : [from][to] = 0
(1) matrix 만들기
let matrix = []
let max = 3
// 가장 큰 정점
for(let i = 0; i < max + 1; i++) {
matrix.push(new Array(max + 1).fill(0))
}
//[[0, 0, 0, 0], [0. 0, 0, 0], [0. 0, 0, 0], [0. 0, 0, 0]]let matrix = new Array(max + 1).fill(0).map(e => new Array(max + 1).fill(0))
//[[0, 0, 0, 0], [0. 0, 0, 0], [0. 0, 0, 0], [0. 0, 0, 0]](2) edges 만들기
matrix[0][1] = 1
matrix[1][0] = 1
matrix[0][2] = 1
matrix[2][0] = 1
matrix[0][3] = 1
//단방향
matrix[1][2] = 1
matrix[2][1] = 12) 인접 리스트(adjacency list)
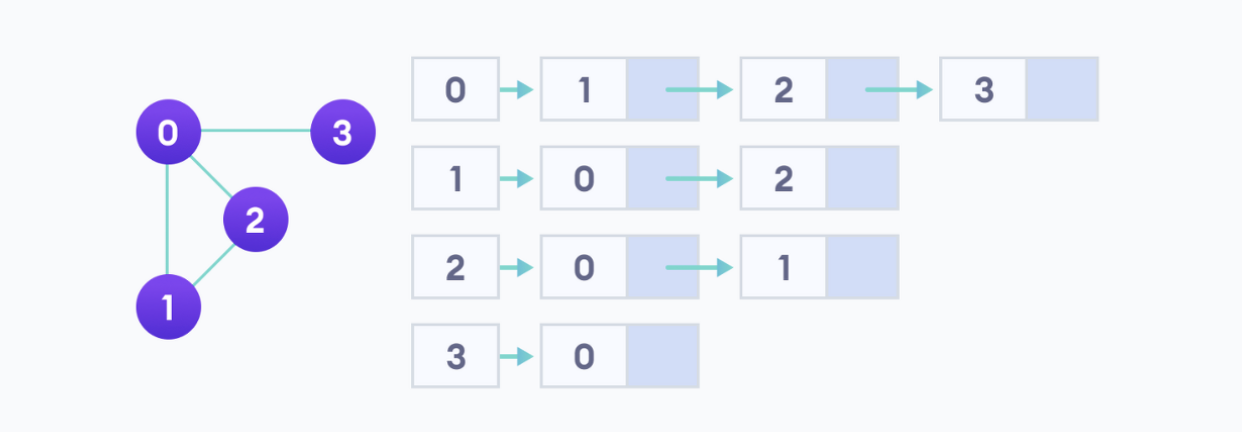
- 그래프의 각 정점에 인접한 정점을 연결 리스트로 표현하는 방법
- 연결 리스트의 노드는 인접 정점 정보를 저장하는데, 그래프에는 이러한 각 인접 리스트에 대한 헤더 포인터를 갖는 배열로 갖음
*정점의 번호만 알고 있으면 각 정점의 연결 리스트에 쉽게 접근 가능
(1) adjList 만들기
let max = 3
// 가장 큰 정점
let adjList = {}
for(let i = 0; i < max + 1; i++) {
adjList[i] = []
}
//{0 : [], 1 : [], 2 : [], 3 : []}(2) edges 만들기
adjList[0].push(1)
adjList[0].push(2)
adjList[0].push(3)
adjList[1].push(0)
adjList[1].push(2)
adjList[2].push(0)
adjList[2].push(1)
adjList[3].push(0)3. 예제 : 내비게이션 시스템
1) 비가중치 그래프
정점: 서울, 대전, 부산
간선: 서울—대전, 대전—부산, 부산—서울
let isConnected = {
seoul: {
busan: true,
daejeon: true
},
daejeon: {
seoul: true,
busan: true
},
busan: {
seoul: true,
daejeon: true
}
}
console.log(isConnected.seoul.daejeon) // true
console.log(isConnected.daejeon.busan) // true- 간선 : 차로 이동할 수 있음을 의미
*이어져 있음만 알 수 있고, 얼마나 떨어져 있는지는 파악 불가 - 비가중치 그래프 : 가중치(연결의 강도가 얼마나 되는지)가 적혀 있지 않은 그래프
2) 가중치 그래프
정점: 서울, 대전, 부산
간선: 서울—140km—대전, 대전—200km—부산, 부산—325km—서울
- 가중치 그래프 : 간선에 연결정도(거리 등)를 표현한 그래프
4. 관련 용어
- 무(방)향그래프(undirected graph) : 양방향으로 이어짐
- 단방향(directed) : 단방향만 이동 가능
- 진입차수(in-degree) / 진출차수(out-degree): 한 정점에 들어오고(진입) 나가는(진출) 간선이 몇 개인지
- 인접(adjacency): 간선이 직접 이어진 경우
- 자기 루프(self loop): 정점에서 진출하는 간선이 곧바로 자기 자신에게 진입하는 경우
*다른 정점을 거치지 않음 - 사이클(cycle): 한 정점에서 출발하여 다시 해당 정점으로 돌아갈 수 있는 경우
그래프의 탐색 기법
- 그래프의 탐색 : 하나의 정점에서 시작하여 그래프의 모든 정점들을 한번씩 방문(탐색)하는 것을 목적으로 함
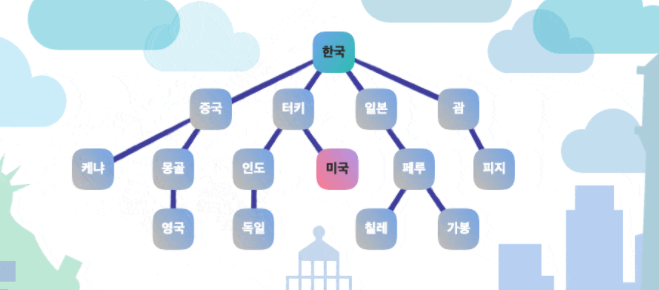
BFS : 한국에서 미국으로 가는 가장 빠른 경로
- 한국 > 중국 > 한국 > 터키 > 한국 > 일본 > 한국 > 괌
- 한국 > 중국 > 케냐 > 한국 > 중국 > 몽골 > 한국 > 터키 > 인도 > 한국 > 터키 > 미국
- 최단 경로 : 한국 > 터키 > 미국
DFS : 한국에서 미국으로 가는 경로
- 한국 > 중국 > 케냐 > 한국 > 중국 > 몽골 > 영국
- 한국 > 터키 > 인도 > 독일 > 한국 > 터키 > 미국 : 최단 경로
- 최단 경로 : 한국 > 터키 > 미국
1. BFS(Breadth-First Search)
- 가까운 정점부터 탐색
- 더는 탐색할 정점이 없을 때, 그 다음 떨어져 있는 정점을 순서대로 방문
- 너비를 우선적으로 탐색한다고 하여 Breadth-First Search(너비 우선 탐색)이라 함
- 주로 두 정점 사이의 최단 경로를 찾을 때 사용
- 경로를 하나씩 전부 방문한다면, 최악의 경우에는 모든 경로를 다 살펴보아야 함
- Queue(with while 반복문)와 짝궁
2. DFS(Depth-First Search)
- 하나의 경로를 끝까지 탐색
- 찾는 정점이 아니라면 다음 경로로 넘어가 탐색
- 깊이를 우선적으로 탐색한다고 하여 Depth-First Search(깊이 우선 탐색)이라 함
- 한 정점에서 시작해서 다음 경로로 넘어가기 전에 해당 경로를 완벽하게 탐색할 때 사용
- BFS보다 탐색 시간은 오래 걸리지만 모든 노드를 완전히 탐색 가능
- Stack(with 재귀함수)와 짝궁
