[algorithm] Dijkstra

Dijkstra 알고리즘은 양의 가중치만 있는 그래프에서 한 노드에서 모든 노드까지의 최단 경로를 찾는 알고리즘이다.
우선순위 큐를 이용하여 구현할 경우 시간복잡도가 $O((V+E)logV)$가 된다.

• V : 정점의 개수
• E : 간선의 개수

구현 예시는 아래 그래프에서 dijkstra 알고리즘을 사용하여 최단 경로를 찾는 예시이다.

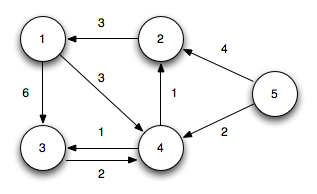
구현1 (인접행렬로 구현된 그래프)

#include <iostream>
#include <vector>
#include <queue>
using namespace std;

#define INF (int)1e9

struct Z {
    int idx;
    int dist;

    bool operator>(const struct Z& other) const {
        return dist > other.dist;
    }
};

void dijkstra(vector<vector<int>>& v, vector<int>& dist) {
    priority_queue<Z, vector<Z>, greater<Z>> pq;
    for (int i = 0; i < dist.size(); i++) {
        pq.push({ i, dist[i] });
    }

    while (!pq.empty()) {
        struct Z top = pq.top();
        pq.pop();

        if (top.dist > dist[top.idx]) continue;

        for (int i = 0; i < v.size(); i++) {
            if (v[top.idx][i] == 0) continue;
            int newDist = dist[top.idx] + v[top.idx][i];
            if (newDist < dist[i]) {
                dist[i] = newDist;
                pq.push({ i, dist[i] });
            }
        }
    }
}

int main() {
    vector<vector<int>> v{
        { 0, 0, 6, 3, 0 },
        { 3, 0, 0, 0, 0 },
        { 0, 0, 0, 2, 0 },
        { 0, 1, 1, 0, 0 },
        { 0, 4, 0, 2, 0 }
    };
    vector<int> dist({ INF, INF, INF, INF, 0 });

    dijkstra(v, dist);
    for (auto& e : dist) cout << e << "\t";
    cout << endl;
    return 0;
}

구현2 (인접리스트로 구현된 그래프)

#include <iostream>
#include <vector>
#include <queue>
using namespace std;

#define INF (int)1e9

struct Z {
    int idx;
    int dist;

    bool operator>(const struct Z& other) const {
        return dist > other.dist;
    }
};

void dijkstra(vector<vector<Z>>& v, vector<int>& dist) {
    priority_queue<Z, vector<Z>, greater<Z>> pq;
    for (int i = 0; i < dist.size(); i++) {
        pq.push({ i, dist[i] });
    }

    while (!pq.empty()) {
        struct Z top = pq.top();
        pq.pop();

        if (top.dist > dist[top.idx]) continue;

        for (int i = 0; i < v[top.idx].size(); i++) {
            int newDist = dist[top.idx] + v[top.idx][i].dist;
            int destIdx = v[top.idx][i].idx;
            if (newDist < dist[destIdx]) {
                dist[destIdx] = newDist;
                pq.push({ destIdx, dist[destIdx] });
            }
        }
    }
}

int main() {
    vector<vector<Z>> v{
        {{2, 6}, {3, 3}},
        {{0, 3}},
        {{3, 2}},
        {{1, 1}, {2, 1}},
        {{1, 4}, {3, 2}}
    };
    vector<int> dist({ INF, INF, INF, INF, 0 });

    dijkstra(v, dist);
    for (auto& e : dist) cout << e << "\t";
    cout << endl;
    return 0;
}