문제 링크 - https://www.acmicpc.net/problem/1041
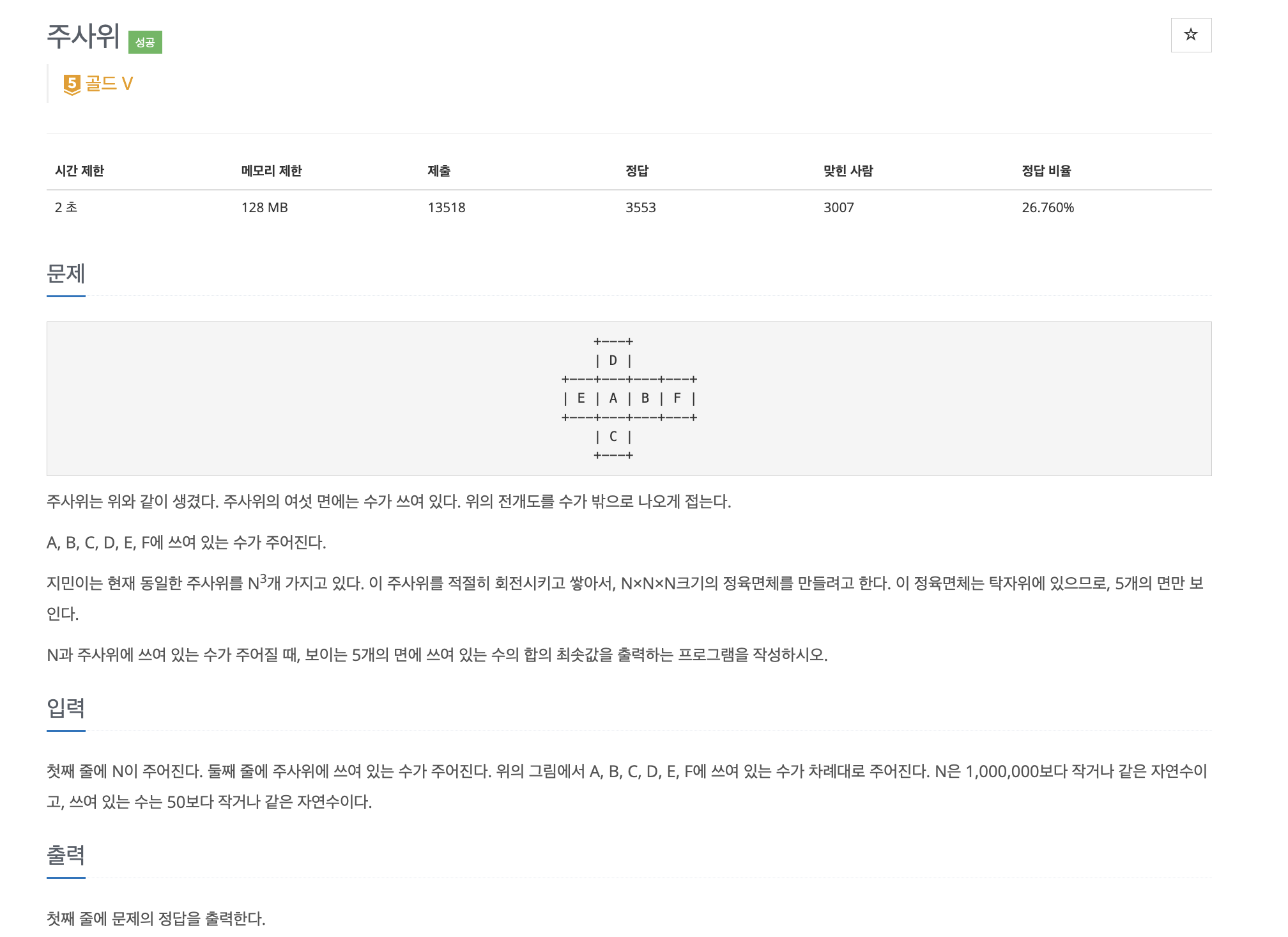
🌱 문제
🌱 풀이
규칙 찾기
- 매우 헤맸던 문제이다 ....
- 우선 NxNxN개의 주사위가 모인 정육면체를 살펴보면, 주사위의 3가지 경우로 정육면체의 다섯 겉면을 나타낼 수 있다. (문제에서 바닥면은 안보인다고 했으므로)
1. 주사위가 한개의 면이 보이는 경우 (노란색)
2. 주사위가 두개의 면이 보이는 경우 (초록색)
3. 주사위가 세개의 면이 보이는 경우 (하늘색)
- 그림으로 나타내보았다.
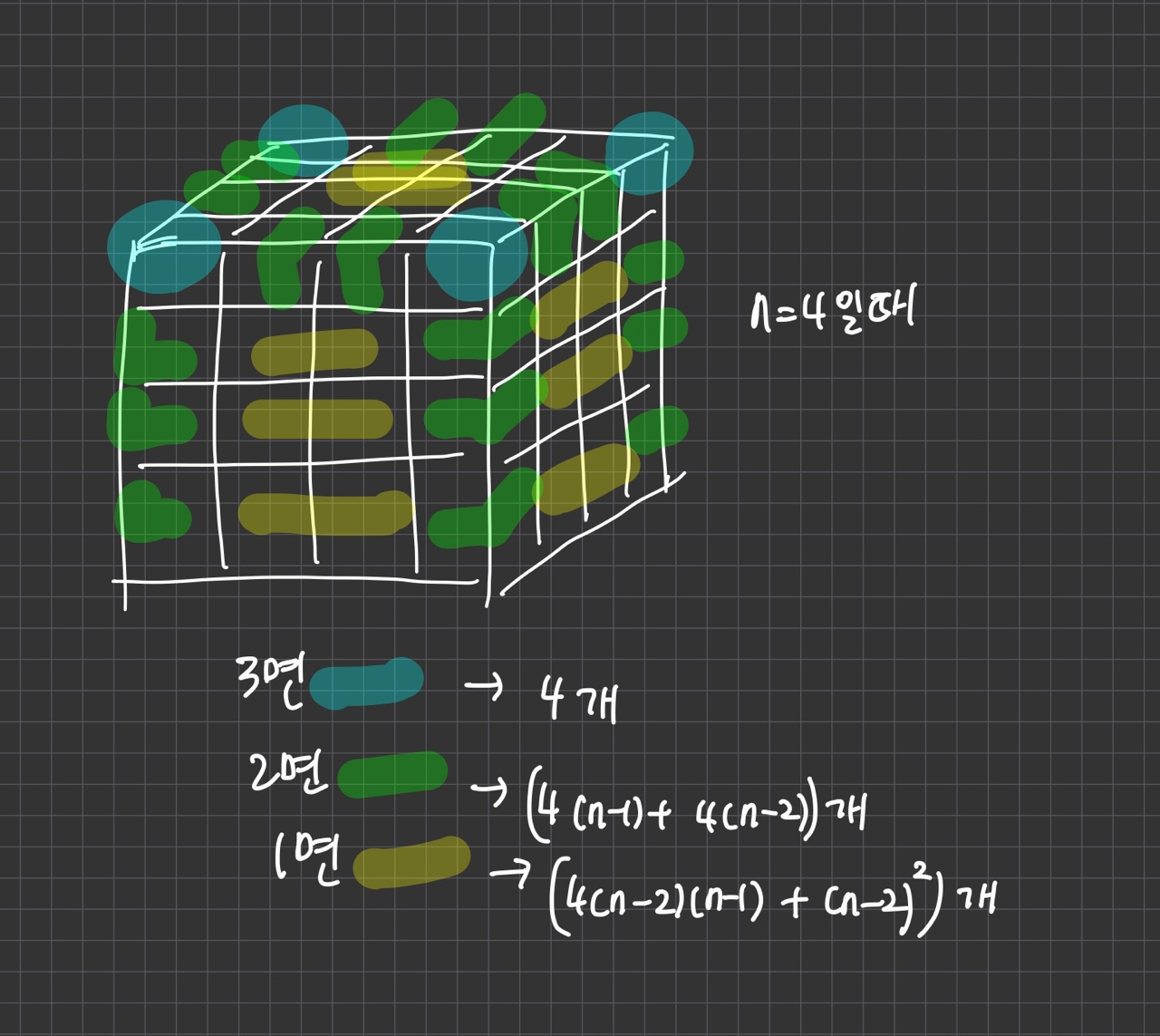
- 각각의 경우에 해당하는 갯수가 몇개인지 일반화된 식을 꾸역꾸역 찾아보았다. (사진에 표시)
- 이 부분은 사람마다 일반화하는 과정이 다를것이다. (= 전개해서 계산하면 같겠지만 식을 쓰는 과정이 다르다는 뜻)
이웃하는 면의 최솟값 구하기 (1개, 2개, 3개의 경우)
- 이부분은 떠올리기 어려워서 구글링을 참고했다.
- 전개도를 접은 모습을 떠올리면서 이웃하는 면들의 인덱스에 어떤 패턴이 있는지 살펴보았다. (구하는 과정은 주석 참고)
long one = Long.MAX_VALUE;
long two = Long.MAX_VALUE;
long three = 0;
long max = 0;
long sum = 0;
for (int i = 0; i < 6; i++) {
one = Math.min(one, arr[i]);
max = Math.max(max, arr[i]);
sum += arr[i];
}
for (int i = 0; i < 6; i++) {
for (int j = 0; j < 6; j++) {
if (i + j != 5 && i != j)
two = Math.min(two, arr[i] + arr[j]);
}
}
for (int i = 0; i < 3; i++) {
three += Math.min(arr[i], arr[5 - i]);
}
주의할 점
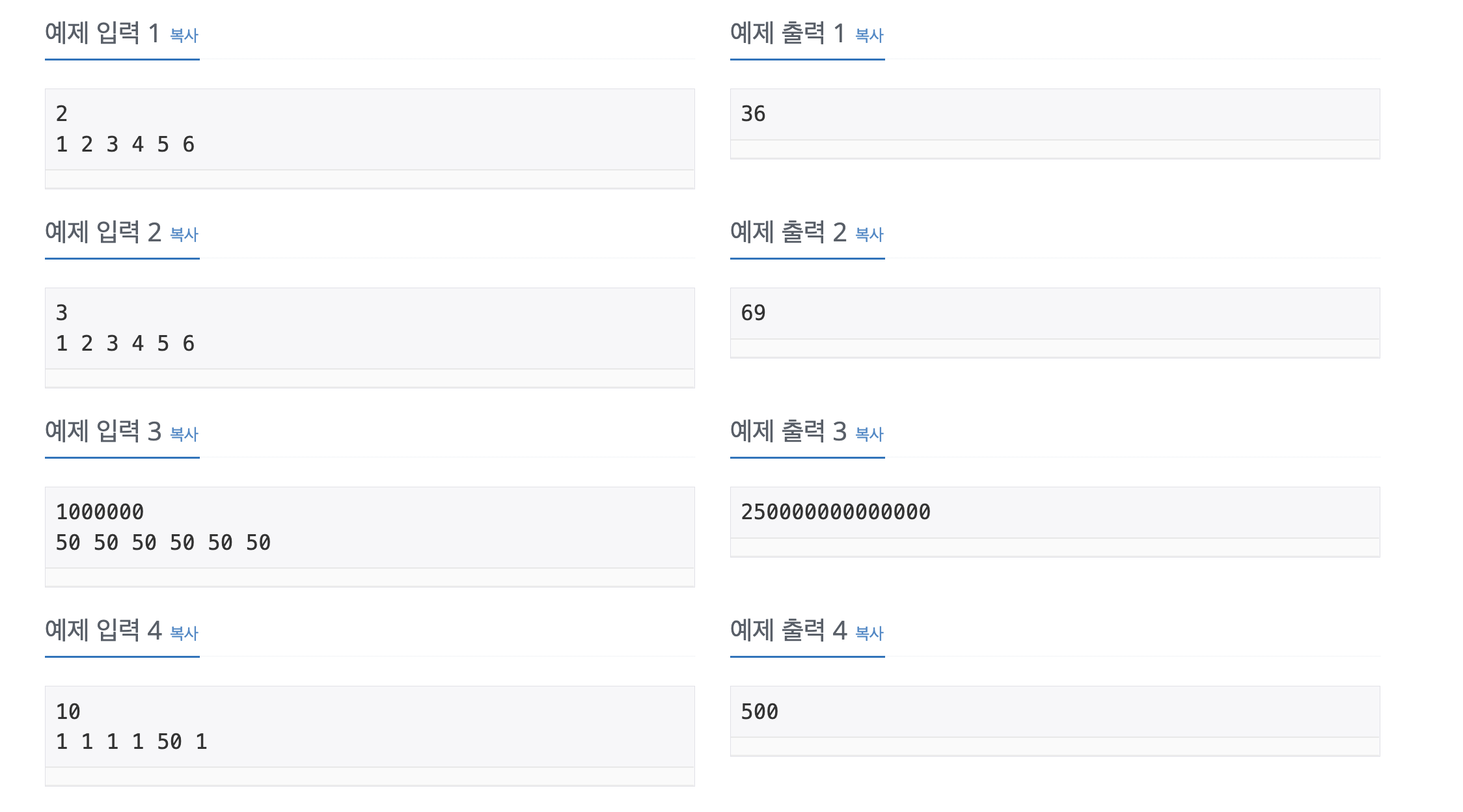
- 예제 3번의 답이 계속 이상하게 나왔었다.
- 예제 3번의 경우처럼 int범위 이상의 값이 정답이 될 수 있기 때문에 변수 answer, one, two, three는 long형으로 선언하였다. 하지만 N은 long일 필요가 없다고 생각해서 int로 유지했는데 이것이 틀린 원인이었다.
answer = three * 4 + two * (4 * (n - 1) + 4 * (n - 2)) + one * ((n - 2) * (n - 1) * 4 + (n - 2) * (n - 2)); 를 계산하는 과정을 보면 마지막 항은 (n-2)x(n-2)이므로 n의 자료형에 의존하고 있는데, int x int 계산을 한 값이 인트범위를 넘어가면 오버플로우가 나서 답이 들어오지 않게 된다.- 그래서 n도 long형으로 바꿔주어서 답이 나오게 되었다. !
🌱 전체 코드
package Dec_week01;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class boj_1041 {
static long n;
static long[] arr;
static long answer;
public static void main(String[] args) throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
n = Integer.parseInt(br.readLine());
arr = new long[6];
st = new StringTokenizer(br.readLine());
for (int i = 0; i < 6; i++) {
arr[i] = Integer.parseInt(st.nextToken());
}
long one = Long.MAX_VALUE;
long two = Long.MAX_VALUE;
long three = 0;
long max = 0;
long sum = 0;
for (int i = 0; i < 6; i++) {
one = Math.min(one, arr[i]);
max = Math.max(max, arr[i]);
sum += arr[i];
}
for (int i = 0; i < 6; i++) {
for (int j = 0; j < 6; j++) {
if (i + j != 5 && i != j)
two = Math.min(two, arr[i] + arr[j]);
}
}
for (int i = 0; i < 3; i++) {
three += Math.min(arr[i], arr[5 - i]);
}
if (n == 1) {
answer = sum - max;
} else {
answer = three * 4 + two * (4 * (n - 1) + 4 * (n - 2)) + one * ((n - 2) * (n - 1) * 4 + (n - 2) * (n - 2));
}
System.out.println(answer);
}
}



