[백준/java] 10986. 나머지의 합

문제 링크 - https://www.acmicpc.net/problem/10986

🌱 문제

---

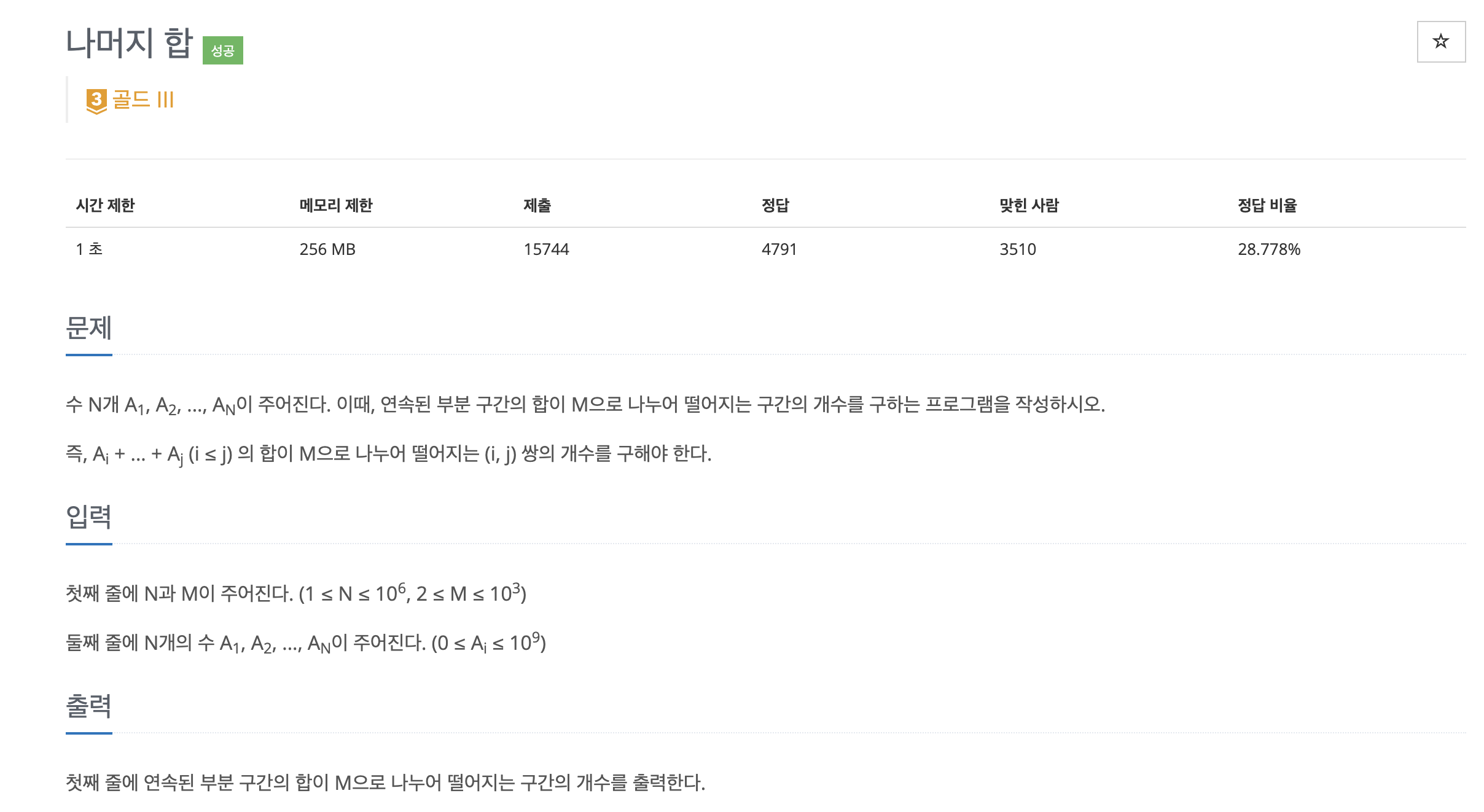
🌱 풀이

처음 시도한 방법

• 2차원 배열에 누적합을 전부 기록하였다. 즉 sum[i][j] : i번부터 j번까지의 누적합.
• 그리고 기록과 동시에 그 값이 M으로 나누어떨어지는지를 검사하여 정답 갯수에 추가하였다.
• 하지만 당연하게도 1<=N<=10^6, 2<=M<=10^3, 0<=Ai<=10^9 이기 때문에 시간초과가 날 예정인 방법이었고, sum = new int[N][N];에서 이미 메모리 초과가 났다.

for (int i = 0; i < N; i++) {
			for (int j = i; j < N; j++) {
				if (i == j) {
					sum[i][j] = arr[i];
					if(sum[i][j]%M==0) answer++;
					
					continue;
				}else {
					sum[i][j]=sum[i][j-1]+arr[j];
					if(sum[i][j]%M==0) answer++;
				}
			}
		}

---

풀이 과정

도저히 모르겠어서 구글링을 통해 이해하고 다시 풀도록 했다.

• 우선 sum[i]: 1번째부터 i번째 수 까지의 누적합 이라고 하자.
• i부터 j까지의 누적합을 구하려면 sum[i]-sum[j-1]와 식으로 찾을 수 있다.
• 문제에서 찾고자 하는건 (sum[i]-[j-1]) % M == 0 이 되는 구간의 갯수이다.

---

mod 분배법칙 사용

• (sum[i]-sum[j])%M==0 은 mod연산의 분배법칙을 통해 sum[i]%M-s[j]%M==0 으로 나타낼 수 있다.
• 이것은 다시 sum[i]%M == sum[j]%M 으로 나타낼 수 있고, 이를 만족하는 (i,j)의 순서쌍이 몇개인지 구하면 된다.
• 즉 누적합을 M으로 모드를 취한 값이 같은 값 중에 2개를 순서없이 뽑는 경우의 수를 구하면 된다.

---

누적합을 M으로 모드를 취한 값이 같의 수가 각각 몇개 있는지 기록

• remainder 배열에 기록하였다.
• 원래는 sum에다가 바로 mod연산을 취하지 않고,

int index = sum%M;
remainder[index]++;

과 같은 식으로 했는데, 런타임 에러 (ArrayIndexOutOfBounds)가 나서 sum에 매번 mod연산을 취한값으로 갱신해주었다. (저기서 왜 인덱스오류인지는 모르겠다ㅠ)

for (int i = 0; i < N; i++) {
			int num = Integer.parseInt(st.nextToken());
			sum += num;
			sum%=M; // sum : i번째의 누적합을 M으로 mod취한 값 
			remainder[sum]++; // sum의 값이 0~M-1 것이 각각 몇개인지 저장
		}

---

remainder 배열의 각 결과에서 '순서를 고려하지 않고 2개 고르는 경우의수'의 합 구하기

• remainder[0] ~ reaminder[M-1]에서 나오는 각각의 경우의 수의 합이 정답이 된다.

// i번째까지의 누적합을 M으로 모드 취한 결과에서 (remainder)
		// 각 결과마다 2개씩 고를 수 있는 조합의 갯수 구하기
		for (int i = 0; i < M; i++) {
			int size = remainder[i];
			long combi = (long) size * (size - 1) / 2; // nC2 공식에 의해
			answer += combi;
		}
		answer += remainder[0];

		System.out.println(answer);

---

🌱 처음시도한 코드 (실패)

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

// 10986. 나머지 합 
public class Main {
	static int N, M;
	static int arr[];
	static int sum[][];
	static int answer;

	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st = new StringTokenizer(br.readLine());

		N = Integer.parseInt(st.nextToken());
		M = Integer.parseInt(st.nextToken());
		arr = new int[N];
		sum = new int[N][N];

		st = new StringTokenizer(br.readLine());
		for (int i = 0; i < N; i++) {
			arr[i] = Integer.parseInt(st.nextToken());
		}

		for (int i = 0; i < N; i++) {
			for (int j = i; j < N; j++) {
				if (i == j) {
					sum[i][j] = arr[i];
					if(sum[i][j]%M==0) answer++;
					
					continue;
				}else {
					sum[i][j]=sum[i][j-1]+arr[j];
					if(sum[i][j]%M==0) answer++;
				}
			}
		}
		
		System.out.println(answer);

	}

}

---

🌱 정답 코드

package Oct_week02;

import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;

// 10986. 나머지 합 
public class boj_10986 {
	static int N, M;
	static int arr[];
	static int remainder[];
	static long answer;

	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringTokenizer st = new StringTokenizer(br.readLine());

		N = Integer.parseInt(st.nextToken());
		M = Integer.parseInt(st.nextToken());
		remainder = new int[M]; // 주의-> M으로 안하고 N으로 해서 계속 ArrayIndex 런타임에러 떳음.
		int sum = 0;

		st = new StringTokenizer(br.readLine());
		for (int i = 0; i < N; i++) {
			int num = Integer.parseInt(st.nextToken());
			sum += num;
			sum%=M; // sum : i번째의 누적합을 M으로 mod취한 값 
			remainder[sum]++; // sum의 값이 0~M-1 것이 각각 몇개인지 저장
		}

		// i번째까지의 누적합을 M으로 모드 취한 결과에서 (remainder)
		// 각 결과마다 2개씩 고를 수 있는 조합의 갯수 구하기
		for (int i = 0; i < M; i++) {
			int size = remainder[i];
			long combi = (long) size * (size - 1) / 2; // nC2 공식에 의해
			answer += combi;
		}
		answer += remainder[0];

		System.out.println(answer);

	}

}