[백준/java] 1309. 동물원

문제 링크 - https://www.acmicpc.net/problem/1309

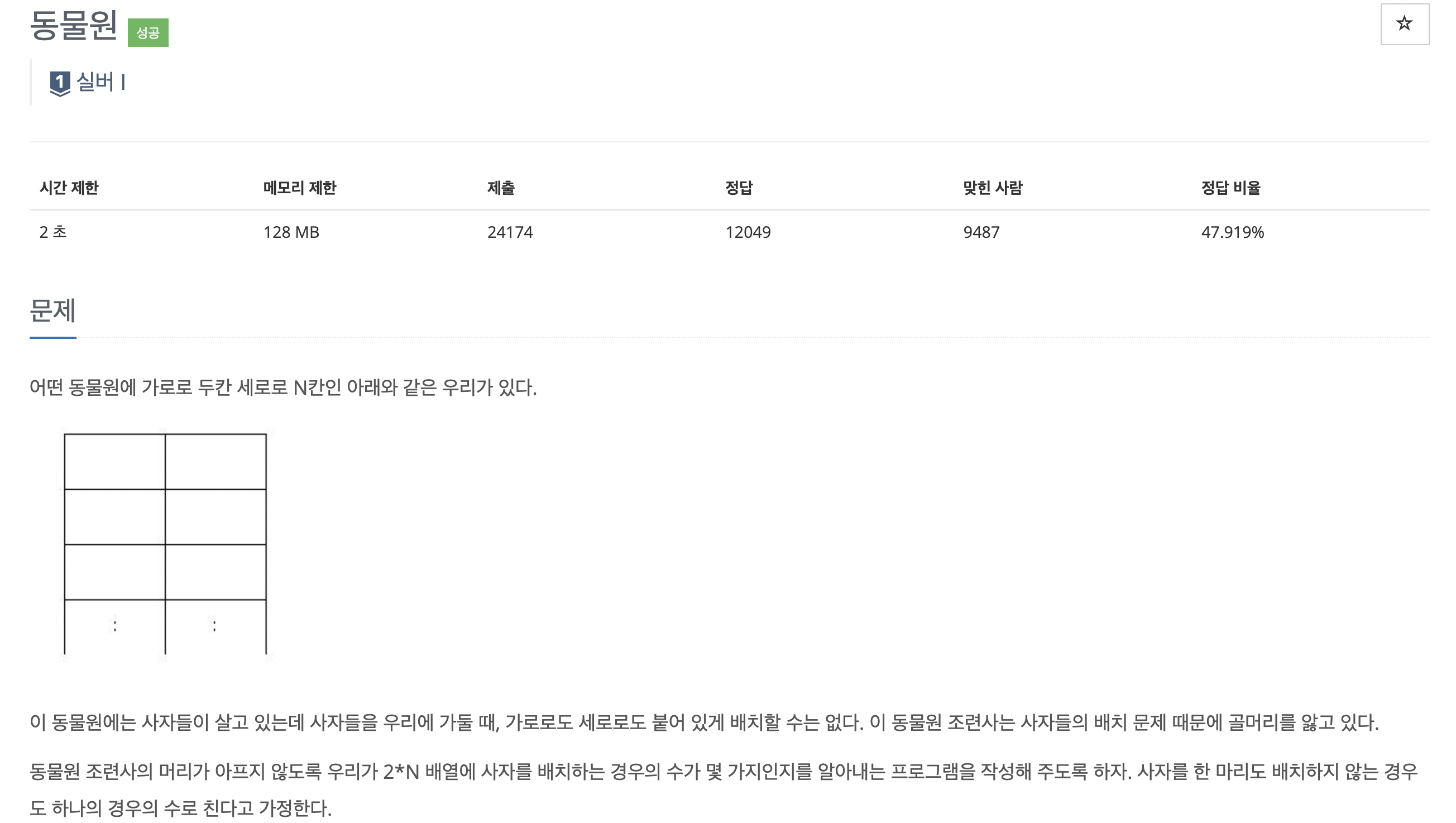
🌱 문제

🌱 풀이

• 처음엔 어떻게 풀어야 할지 감이 안와서 우선 N이 1,2,3,4일때의 정답을 구해보았다.
  • dp[1]=3
  • dp[2]=7
  • dp[3]=17
  • dp[4]=41
• 다음과 같은 결과를 얻을 수 있었다. 어떤 규칙이 있는지 딱히 못떠올리다가 dp[n]=dp[n-1]x2+dp[n-2] 라는 규칙을 찾을 수 있었다.
• 하지만 위 규칙은 어쩌다 발견한 규칙이고, 어떻게 해서 저런 식이 나오는지 잘 이해가 안돼서 구글링을 했다.

구글링 도움받아 찾은 규칙

• 우선 다음과 같이 정의하자.
  • dp[n][0]: n번째 행에 사자가 없을때의 경우의 수
  • dp[n][1]: n번째 행의 1열에만 사자가 있을때의 경우의 수
  • dp[n][2]: n번째 행의 2열에만 사자가 있을때의 경우의 수
• N=1일때 초기값인 dp[1][0], dp[1][1], dp[1][2]만 미리 설정한 후, for문을 통해 2,3,4,5,,, N 행까지의 dp값을 찾을 수 있다.
• 이때 규칙은 다음과 같다.

for (int i = 2; i <= N; i++) {
			dp[i][0] = (dp[i - 1][0] + dp[i - 1][1] + dp[i - 1][2])%9901; 
            // 이전행에 사자가 없어도 되고 1열에 있어도 되고, 2열에 있어도 됨.
			dp[i][1] = (dp[i - 1][0] + dp[i - 1][2])%9901
            // 이전행에 사자가 없거나 2열에만 있어야 함 
			dp[i][2] = (dp[i - 1][0] + dp[i - 1][1])%9901;
            // 이전행에 사자가 없거나 1열에만 있어야 함.
}

🌱 코드

package week08.boj_1309;

import java.util.Scanner;

//1309. 동물원 
public class Somyeong {
	static int N;
	static int[][] dp;

	public static void main(String[] args) {
		Scanner sc = new Scanner(System.in);
		N = sc.nextInt();
		dp = new int[N + 1][3];

		// dp[i][0]: i번 행의 1열 2열에 둘다 사자가 없는 경우
		// dp[i][1]: i번 행의 1열에만 사자가 있는 경우
		// dp[i][2]: i번 행의 2열에만 사자가 있는 경우
		
        //초기값 설정
		dp[1][0] = 1;
		dp[1][1] = 1;
		dp[1][2] = 1;

		for (int i = 2; i <= N; i++) {
			dp[i][0] = (dp[i - 1][0] + dp[i - 1][1] + dp[i - 1][2])%9901;
			dp[i][1] = (dp[i - 1][0] + dp[i - 1][2])%9901;
			dp[i][2] = (dp[i - 1][0] + dp[i - 1][1])%9901;
		}
		System.out.println((dp[N][0]+dp[N][1]+dp[N][2])%9901);
	}

}