🌱 문제

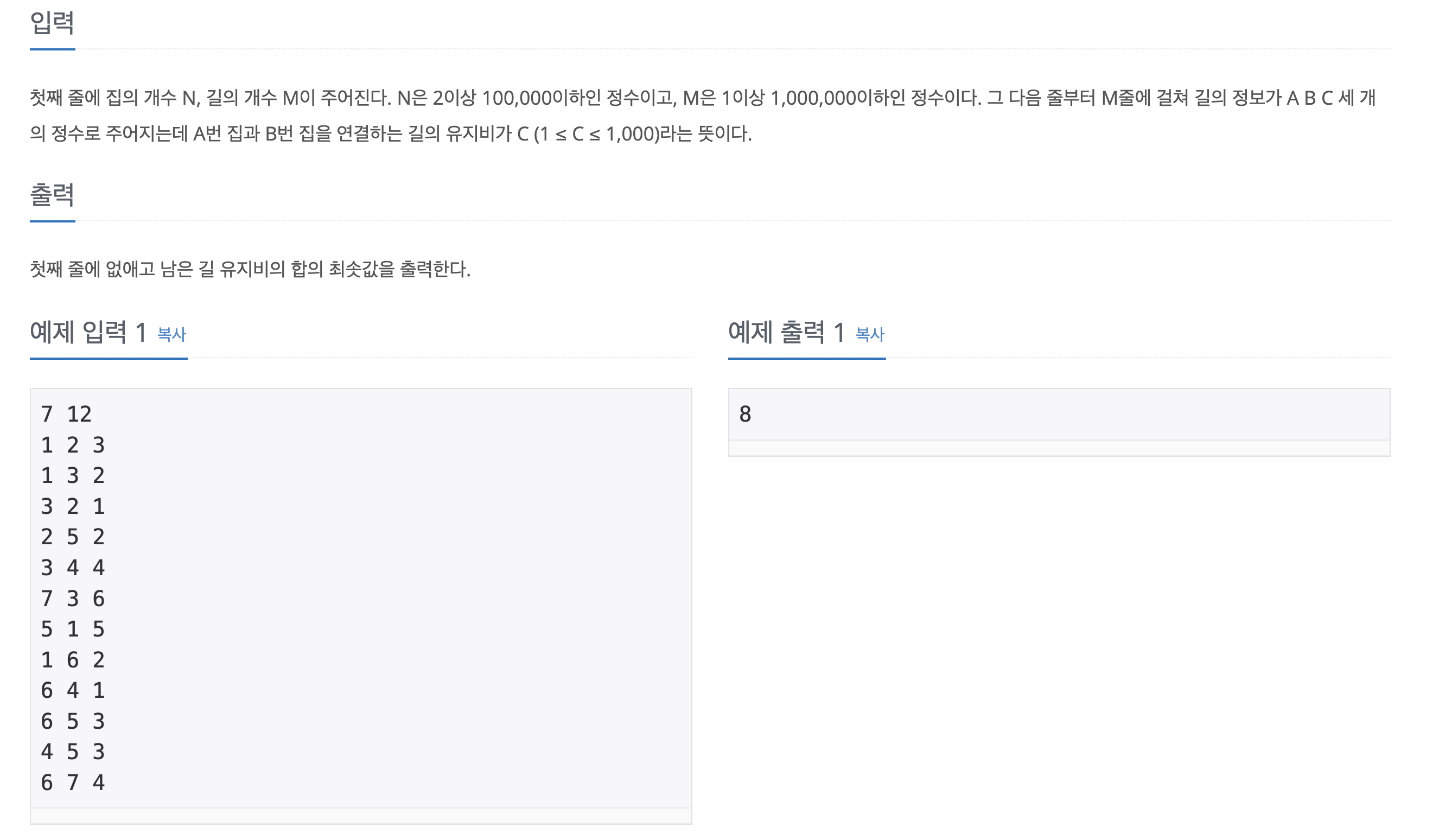
🌱 풀이
- 문제에서 구하라고 하는 것을 요약하면, 최소 스패닝 트리를 구해서 간선 비용 합의 최솟값을 구하는 것이다.
- 이때 마을을 두개로 분할해야 하는데, 문제를 읽어보면 별 다른 조건 없이 두개로 마을을 분할하기만 되므로, 최소 스패닝 트리를 만족하는 상태에서 가장 비용이 큰 간선을 하나 제외했을 때 정답을 구할 수 있겠다고 생각했다.
- 생각했던 방법대로 구현하고 채점해보니 바로 맞았당 .
최소 스패닝 트리 개념
- Spanning Tree: 그래프 내의 모든 정점이 간선으로 연결되어 있고, 간선들 사이에 사이클이 없는 그래프.
- MST(Minimum Spanning Tree): Spanning Tree 중에서 사용된 간선들의 가중치 합이 최소인 트리
어떻게 풀까?
- 간적크 간많크
-> 간선이 적으면 크루스칼 알고리즘 / 간선이 많으면 프림 알고리즘- 나는 크루스칼 방식으로 풀었다. (문제에서 N에 비해 M이 그렇게 많진 않았기 때문에 .. )
- 먼저 간선을 비용 기준 오름차순으로 살펴보면서, 각 간선을 연결하고 있는 두 마을이 연결되어있으면 패스하고, 연결되어있지 않으면 연결시킨 후 비용을 더해나갔다.
- 연결되어있는지 확인은
union&find알고리즘을 통해 확인하였다.
느낀점
크루스칼 알고리즘을 알고 있다면 바로 적용하면 되는 문제였다.
프림은 기억이 잘 안나는데, 다음에 프림으로도 풀어봐야겠다.
🌱 코드
package week16.boj_1647;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayList;
import java.util.Collections;
import java.util.StringTokenizer;
public class Somyeong {
static class Info implements Comparable<Info>{
int x,y,cost;
public Info(int x, int y ,int cost) {
this.x=x;
this.y=y;
this.cost=cost;
}
public int compareTo(Info o) { // cost기준 오름차순 정렬
return this.cost-o.cost;
}
}
static int N,M;
static int parent[];
static int answer,cnt;
public static void main() throws IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
N=Integer.parseInt(st.nextToken());
M=Integer.parseInt(st.nextToken());
parent = new int[N];
ArrayList<Info> edges = new ArrayList<Info>();
ArrayList<Integer> costs = new ArrayList<Integer>();
for(int i=0; i<M; i++) {
st = new StringTokenizer(br.readLine());
int x = Integer.parseInt(st.nextToken());
int y= Integer.parseInt(st.nextToken());
int cost= Integer.parseInt(st.nextToken());
edges.add(new Info(x,y,cost));
}
for(int i=1; i<=N; i++) {
parent[i]=i;
}
cnt=1;
Collections.sort(edges);
for(int i=0; i<M; i++) {
Info cur = edges.get(i);
int x=cur.x;
int y=cur.y;
if(getParent(x)==getParent(y))
continue;
union(x,y);
answer+=cur.cost;
cnt++;
}
System.out.println("cnt: "+cnt);
}
static public int getParent(int x) {
if(parent[x]==x)
return x;
return parent[x]=getParent(parent[x]);
}
static public void union(int x,int y) {
x = getParent(x);
y= getParent(y);
parent[y]=x;
}
}
