트리(Tree)

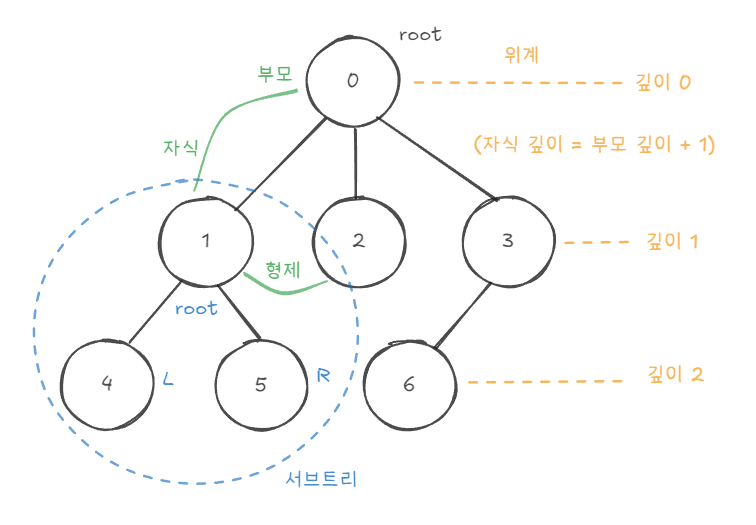
트리(Tree) 자료구조는 그래프(Graph)의 한 형태로 이해할 수 있다. 데이터 간의 계층적 관계를 표현하며, 사이클이 존재하지 않는 구조를 가진다. 그래프에서는 일반적으로 노드(Node)와 간선(Edge)라는 표현을 사용하지만, 트리에서는 주로 정점(Vertex)과 간선(Edge) 또는 부모(Parent)와 자식(Child)이라는 관계 용어가 함께 사용된다.

루트(Root)를 기준으로 위계가 명확하게 구성되며, 어떤 노드든 단 하나의 부모만을 갖는 것이 특징이다. 또한 특정 노드를 기준으로 분리했을 때 그 자체로 또 하나의 트리가 되는 성질을 가진다(서브트리).

이진 트리(Binary Tree)

이진 트리(Binary Tree)는 각 노드가 최대 두 개의 자식 노드를 가지는 트리 구조를 의미한다. 왼쪽(Left)과 오른쪽(Right) 자식으로 구분되며, 트리 자료구조에서 가장 기본적인 형태이다.

이진 트리와 관련해 자주 등장하는 개념이 두 가지 있다.

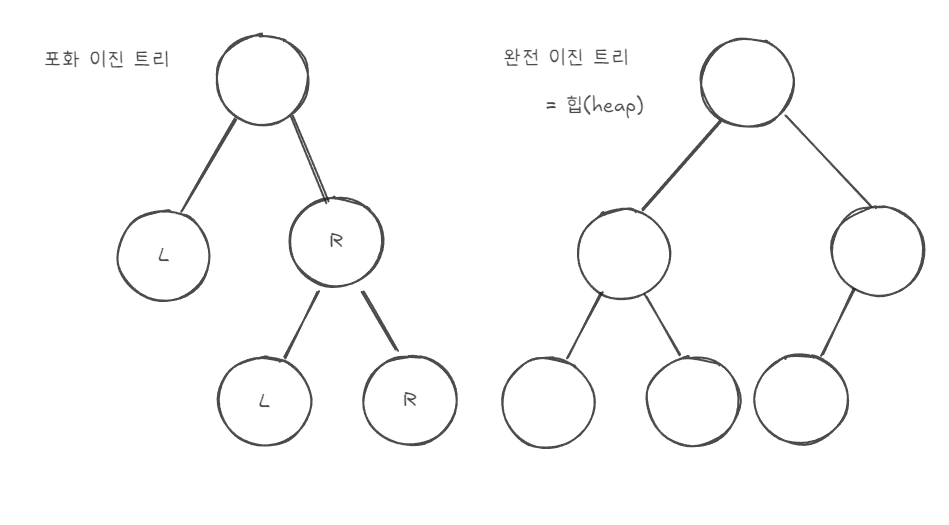
• 포화 이진트리(Full Binary Tree)
  모든 노드가 자식 노드를 0개 또는 2개만 가지는 구조를 말한다.

• 완전 이진트리(Complete Binary Tree)
  노드가 위에서 아래, 그리고 왼쪽부터 오른쪽 순으로 빈틈 없이 채워진 구조를 의미한다.
  단, 마지막 레벨은 완전히 채워지지 않아도 된다.

이러한 기본 개념을 토대로 다음 단계에서는 이진 탐색 트리(Binary Search Tree)의 구조와 특징을 살펴본다.

이진 탐색 트리(BST)

BST는 이진 트리 구조에 정렬 규칙이 적용된 형태이다. 왼쪽 자식(L), 오른쪽 자식(R), 부모(V) 필드를 가진다. 각각의 키들은 이진 검색 트리의 특성을 만족한 상태로 저장된다.

BST 특성

임의의 노드 x에 대해

• x의 왼쪽 서브트리에 있는 모든 노드 y:
  y.value < x.value

• x의 오른쪽 서브트리에 있는 모든 노드 y:
  y.value > x.value

탐색 기준 (L < V < R)이 명확하다.

      10
    /   \
   5     20
  / \    /
 1   7  15

중위 순회(Inorder Traversal)와 정렬

BST의 모든 값을 오름차순으로 정렬된 순서대로 출력하기 위해 중위 트리 순회를 활용할 수 있다.

import sys
input = sys.stdin.readline

# BST 노드 정의
class Node:
    # 인스턴스가 가질 수 있는 속성을 제한
    __slots__ = ('v', 'l', 'r')

    def __init__(self, v):
        self.v = v    # 노드
        self.l = None # 왼쪽
        self.r = None # 오른쪽

# BST 삽입 연산
def insert(root, v):
    # 루트가 없으면 새 노드 생성
    if root is None:
        return Node(v)

    # 값 비교 후 왼/오른쪽으로 재귀 삽입
    if v < root.v:
        root.l = insert(root.l, v)
    else:
        root.r = insert(root.r, v)
    return root

# 중위 순회(Inorder)
def inorder(n, res):
    if n is None:
        return
    inorder(n.l, res)   # 왼쪽 서브트리 탐색
    res.append(n.v)     # 루트 방문
    inorder(n.r, res)   # 오른쪽 서브트리 탐색

# 입력: N개의 값으로 BST 구성
N = int(input().strip())
arr = list(map(int, input().split()))

root = None
for val in arr:
    root = insert(root, val)

# 중위 순회 결과 수집
res = []
inorder(root, res)

# 리스트 언패킹 출력 → 1 2 3 5 7
print(*res)