
오늘도 평화롭게 코테 문제를 풀던 중
아주 평화롭게 계속 테스트 1번만 시간 초과가 떴다.
풀이 자체는 right way로 풀었다 생각했는데 아마 저 1번의 시간초과를 해결하는게 중점인 문제였던거 같다. 그러다가 소수를 구할 때 범위 설정에 관해 알게 되어서 앞으로 소수 구할 일 있으면 써먹고자 기록한다!
소수(Prime Number)
자 소수란 뭐냐
- 소수(Prime Number) : 소수는 1보다 큰 자연수 중 1과 자기자신만을 약수로 가지는 수소수를 구할 때 범위 설정
1. 숫자 전체를 loop(O(n))
그래서 소수를 구할 땐 1과 자기자신을 제외한 약수가 있는지를 체크하면 된다. (있다면 소수가 아니니까)
function solution(n, k) {
let cnt = 0;
n = n.toString(k).split('0');
return n.reduce((acc, e) => {
for(let i = 3; i < e; i++) {
if(e % i == 0) {
cnt++;
i = e;
}
}
cnt == 0 && e != '' && e != 1 ? acc++ : cnt = 0;
return acc;
}, 0)
}이게 문제 풀이였는데, n.reduce가 소수를 구하는 과정이다
보다시피 반복문을 돌며 e까지의 숫자 중 약수가 있는지를 체크하고 약수가 있다면 소수의 카운팅을 늘리지 않고, 약수가 없다면 소수란 소리니 소수 카운팅을 올려준다.
O(n)의 시간복잡도로 탐색을 한다.
근데 저 코드에서의 단점은, 만약 e가 소수라면, 3부터 e 까지 쭉 loop를 돌아야 한다는거다. 시간낭비가 어마어마하겠지? 그래서 시간초과를 맞았다.
2. 숫자의 1/2만큼 loop(O(n))
function solution(n, k) {
let cnt = 0;
n = n.toString(k).split('0');
return n.reduce((acc, e) => {
for(let i = 3; i < e / 2; i++) {
if(e % i == 0) {
cnt++;
i = e;
}
}
cnt == 0 && e != '' && e != 1 ? acc++ : cnt = 0;
return acc;
}, 0)
}아주 간단하게 시간단축을 할 수 있는 두번째 안이다.
O(n)으로 시간복잡도는 동일하지만, 약수는 e / 2를 기준으로 짝을 이루고, 우리는 약수가 하나라도 있는지를 거르기 위함이기에 위 범위 설정이 가능했다.
3. 숫자의 제곱근 만큼 loop(O(√n))
function solution(n, k) {
let cnt = 0;
n = n.toString(k).split('0');
return n.reduce((acc, e) => {
for(let i = 3; i <= Math.sqrt(e) / 2; i++) {
if(e % i == 0) {
cnt++;
i = e;
}
}
cnt == 0 && e != '' && e != 1 ? acc++ : cnt = 0;
return acc;
}, 0)
}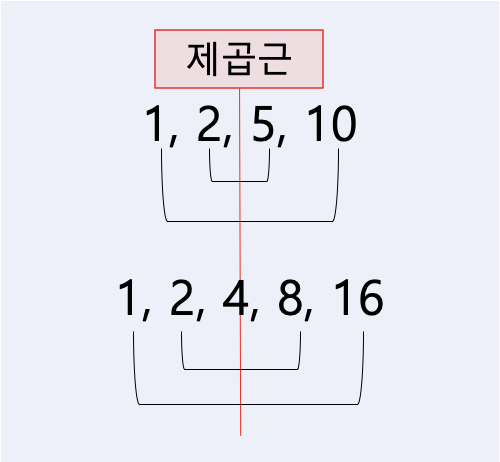
숫자의 약수는 짝으로 존재한다. 아래 그림의 예처럼 쌍을 이루는 약수 중 하나만 찾으면 나머지는 확인하지 않아도 된다.
숫자 20을 예로 20의 약수를 보면
1, 2, 4, 5, 10, 20그 중 1과 자기 자신을 제외한 약수는
2, 4, 5, 10이렇게
2와10, 4와5 처럼 약수는 pair를 갖게 된다.
따라서 제곱근 밑의 수 까지만 계산하면 그 숫자의 pair중 더 낮은 수를 구할 수 있단 소리다.
20의 제곱근은 4.xxxxxxxx 이므로
4까지 loop를 돌리면 2와 4를 찾아낼 수 있다는 말이다.
그러므로 제곱근까지만 확인하면 된다. 이렇게 하면 반복횟수를 더 많이 줄일 수 있다. 시간복잡도는 O(√n ) 이 된다
느낀 점
역시 문제를 해결하는 것이 당연 1번이 되어야 하지만(효율적이여도 답을 못 구해내면 의미가 없으니까)
시간의 효율과 코드의 가독성 역시 너무너무 중요하다는걸 느꼈다.
이 문제 처럼 시간효율을 저격으로 내버리면 난 막힐 것 같고...
아직 많이 부족하다는걸 느꼈다.
하나하나 경험을 쌓고 잊지말고 활용할줄 알아보자 !
