타일링 시리즈

• LV1. 11726: 2xn 타일링
• LV2. 11727: 2xn 타일링 2
• LV3. 2133: 타일 채우기
• LV4. 14852: 타일 채우기 3
• LV5. 아방가르드 타일

문제

https://www.acmicpc.net/problem/11726
2×n 크기의 직사각형을 1×2, 2×1 타일로 채우는 방법의 수를 구하는 프로그램을 작성하시오.
아래 그림은 2×5 크기의 직사각형을 채운 한 가지 방법의 예이다.

풀이

이 문제를 푸는 이유는 프로그래머스 아방가르드 타일링 문제를 풀다가 멘붕이 와서 타일링 문제 기초를 익히려고 풀고있다.

이 문제는 조금만 생각하면 풀 수 있을정도로 정말 간단하다.
n이 1 ~ 4일때를 그림을 그려서 한번 생각해보자.

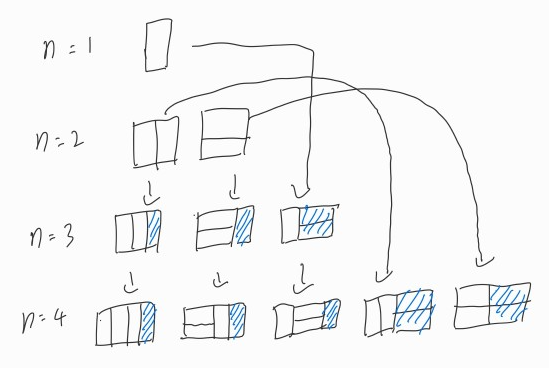
n이 3일때는 n이 2일때 모양들에 파란 면적을 붙인것 + n이 1일때 모양들에 파란 면적을 붙인것
n이 4일때는 n이 3일때 모양들에 파란 면적을 붙인것 + n이 2일때 모양들에 파란 면적을 붙인것

여기서 파란 면적는 n이 1일때 처음 생긴 모양과 n이 2일때 처음 생긴 모양이다.

여기까지 보면 n이 x일때도 쉽게 유추할 수 있고 아래와 같다.

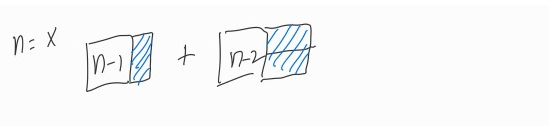
그럼 답은 나왔고 점화식을 세울 수 있게 되었다.

dp[i] = n 이 i일 때 그릴 수 있는 모형의 개수,
dp[1] = 1, dp[2] = 2;
dp[i] = ( dp[i-1] + dp[i-2] ) % 10007

10007로 나누는 이유는 문제에서 결과에 10007을 나누라고 명시되어 있기 때문이다.

코드

const stdin = (process.platform === 'linux'?require('fs').readFileSync(0, 'utf-8'): `8`).trim().split('\n');
const N = +stdin[0];
const dp = Array(1001).fill(0);
dp[1] = 1;
dp[2] = 2;

for (let i = 3; i <= N; i++) {
  dp[i] = (dp[i - 1] + dp[i - 2]) % 10007;
}

console.log(dp[N]);