문제

https://www.acmicpc.net/problem/17070
파이프의 모양을 고려해 0,0에서 시작해서 N-1,N-1에 도착하는 경우의 수를 구하는 문제다.

처음에 파이프는 (0,0)(0,1) 에서 아래의 모양으로 시작한다.

그리고 아래처럼 회전이 가능하다.

각 파이프는 이동할 수 있는 방법이 정해져 있는데 가로 파이프는 아래처럼 이동할 수 있다.

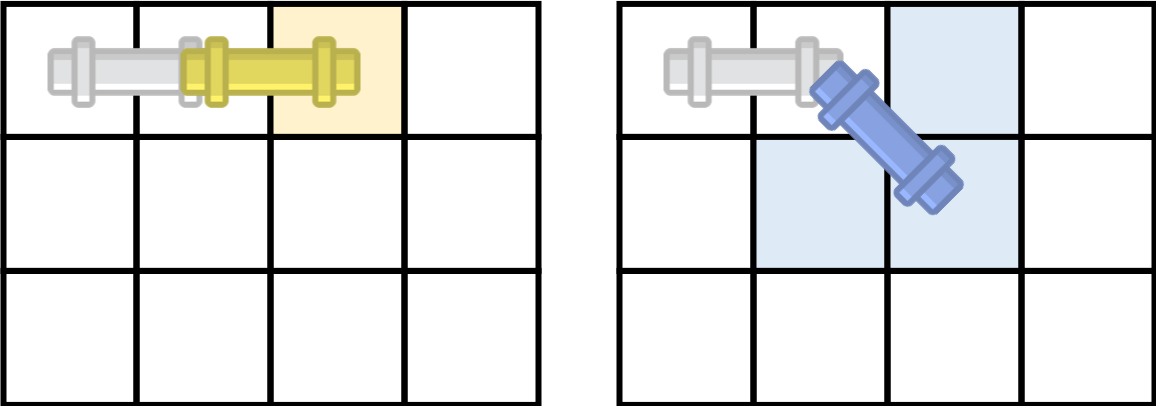
세로파이프는 아래와 같다.

마지막으로 대각선 파이프는 아래처럼 움직일 수 있다.

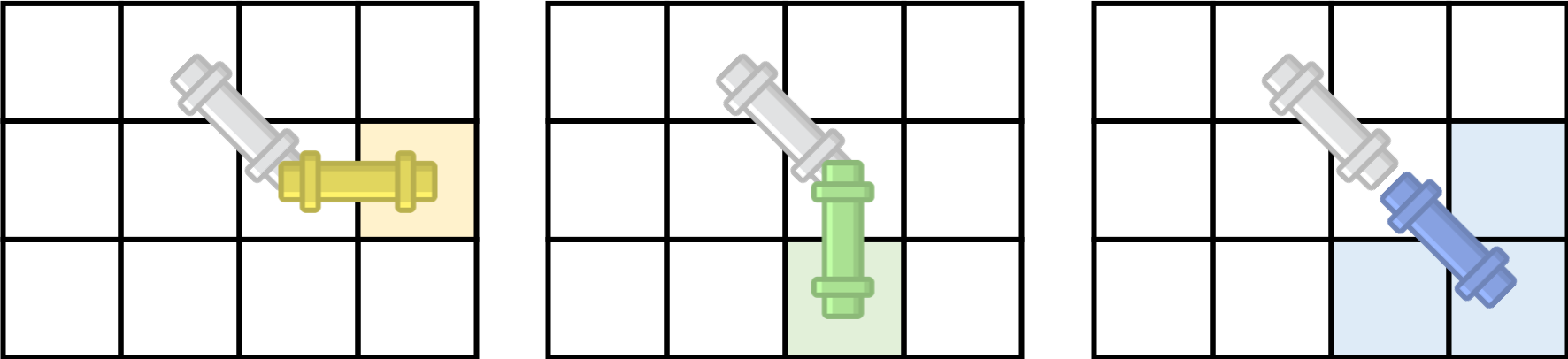
풀이

아마 dp 문제를 많이 풀어봤다면 바로 dp로 푸는방법이 떠오를것이다.
문제를 처음 풀 때 dp로 접근을 했지만 약간 방법이 잘못됐었다.

처음에는 아래처럼 생각을 했다
dp[i][j] = 왼쪽 + 위쪽 + (이동이 가능한 경우) 대각선

하지만 이렇게 하면 이동하지 못하는데 이동이 가능하다 생각하고 이동해버리는 경우가 생긴다.

예를들면 ㅣ 모양과 대각선 모양의 파이프만 아래로 이동이 가능하다.
하지만 위와같이 모든 경우를 다 더해서 dp를 구해버리면 실제 값보다 큰 값이 나오게 돼버린다.

하나더, ㅡ 모양과 대각선 모양의 파이프만 오른쪽으로 이동이 가능하다.
하지만 처음에 생각했던것처럼 ㅣ 모양까지 합치면 정답은 더 커져버린다.

하지만 대각선 모양의 파이프는 아래로도, 오른쪽으로도, 대각선으로도 움직일 수 있다.
그래서 대각선을 구하는 경우에는 전부 더해줘 버리면 된다.

dp 초기화

for (let i = 1; i < N; i++) {
  if (board[0][i] === 1) break;
  dp[0][i][0] = 1;
}

맨 윗줄의 가로로 갈 수 있는경우를 생각해보자.
벽이 나타나기 전에는 계속 가로로 갈 수 있을것이다.
for문에서 예외처리를 해주기 귀찮아서 이렇게 사전에 처리해줬다.

dp 구하기

for (let i = 1; i < N; i++) {
  for (let j = 1; j < N; j++) {
    if (board[i][j] === 1) continue;

    // (0) 왼쪽에서 오는거: 왼쪽의 대각선, 왼쪽의 왼쪽에서 온걸 더해줌
    dp[i][j][0] = dp[i][j - 1][0] + dp[i][j - 1][2];
    // (1) 위에서 오는거: 위의 대각선, 위의 위에서 온거 더해줌
    dp[i][j][1] = dp[i - 1][j][1] + dp[i - 1][j][2];

    if (board[i - 1][j] === 0 && board[i][j - 1] === 0) {
      // (2) 대각선에서 오는거: 대각선의 왼쪽, 대각선의 세로, 대각선의 대각선 더해줌
      dp[i][j][2] = dp[i - 1][j - 1][0] + dp[i - 1][j - 1][1] + dp[i - 1][j - 1][2];
    }
  }
}

dp[i][j][x] -> x에 대해
0 - 왼쪽에서 오는경우
1 - 위에서 오는경우
2 - 대각선에서 오는경우

dp[i][j][x] 에 대해서는 위와 같다.

처음에 말한것처럼 왼쪽과 위에서 오는경우 각각 위와 왼쪽에서 오는 경우를 제외해줘야 한다.
안그러면 실제로는 올 수 없는데 올 수 있다고 기록해 버리기 때문이다.
그 결과 dp 식은 아래와 같아진다.

dp[ i ][ j ][왼쪽] = dp[ i ][ j - 1 ][왼쪽] + dp[ i ][ j - 1 ][대각];
dp[ i ][ j ][위쪽] = dp[ i - 1 ][j][왼쪽] + dp[ i - 1 ][ j ][대각];
dp[ i ][ j ][대각] = dp[ i - 1 ][ j - 1 ][왼쪽] + dp[ i - 1 ][ j - 1 ][위쪽] + dp[ i - 1 ][ j - 1 ][대각];

결과는 이렇게 구한 마지막 dp(N-1, N-1) 을 모두 더해 출력해주면 된다.

전체 코드

//const stdin = require('fs').readFileSync(0, 'utf-8').trim().split('\n');
//prettier-ignore
const stdin = ` 
6
0 0 0 0 0 0
0 1 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
0 0 0 0 0 0
`.trim().split('\n');
//prettier-ignore
const input = (() => { let l = 0; return () => stdin[l++].split(' ').map(Number);})();

const N = +input();
const board = Array.from({ length: N }, () => input());
// 왼쪽, 대각선, 위에서 온걸 각각 저장해야함.
// 0: 왼쪽, 1: 위, 2: 대각선
const dp = Array.from({ length: N }, () => Array.from({ length: N }, () => [0, 0, 0]));

// 처음 맨위 가로줄은 벽을 만나기 전까지 1로 채워줌
for (let i = 1; i < N; i++) {
  if (board[0][i] === 1) break;
  dp[0][i][0] = 1;
}

for (let i = 1; i < N; i++) {
  for (let j = 1; j < N; j++) {
    if (board[i][j] === 1) continue;

    // (0) 왼쪽에서 오는거: 왼쪽의 대각선, 왼쪽의 왼쪽에서 온걸 더해줌
    dp[i][j][0] = dp[i][j - 1][0] + dp[i][j - 1][2];
    // (1) 위에서 오는거: 위의 대각선, 위의 위에서 온거 더해줌
    dp[i][j][1] = dp[i - 1][j][1] + dp[i - 1][j][2];

    if (board[i - 1][j] === 0 && board[i][j - 1] === 0) {
      // (2) 대각선에서 오는거: 대각선의 왼쪽, 대각선의 세로, 대각선의 대각선 더해줌
      dp[i][j][2] = dp[i - 1][j - 1][0] + dp[i - 1][j - 1][1] + dp[i - 1][j - 1][2];
    }
  }
}

const result = dp[N - 1][N - 1][0] + dp[N - 1][N - 1][1] + dp[N - 1][N - 1][2];
console.log(result);