데이터베이스 정규화

참고

데이터베이스 정규화
[Database] 7. 정규화(Normalization)

---

이상현상

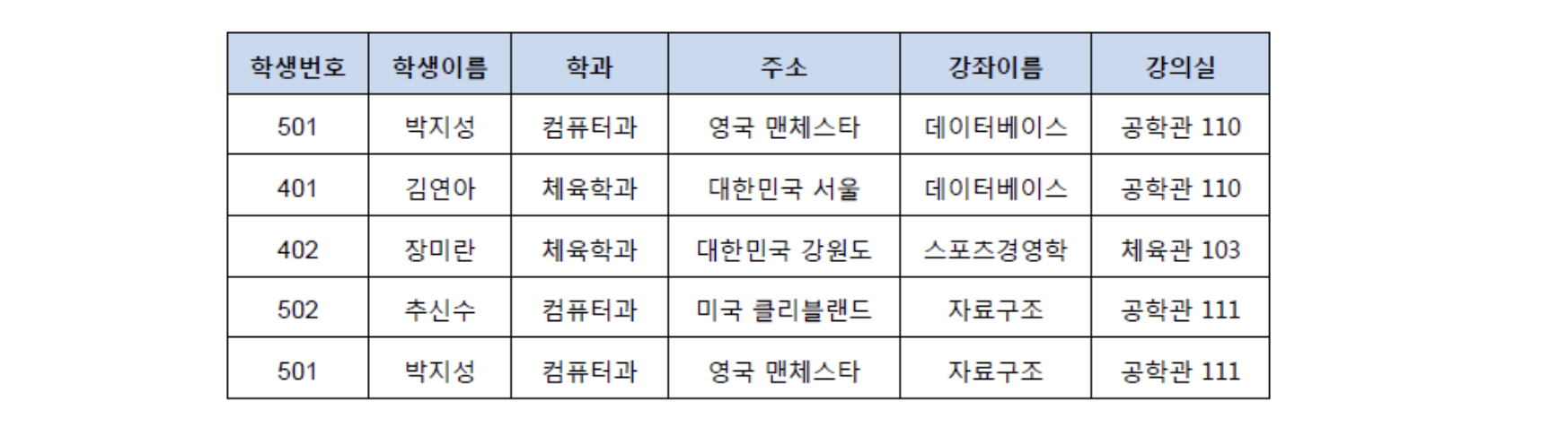
• 삭제 이상
  튜플을 삭제할 때 저장되어 있는 다른 정보들도 함께 삭제되어 연쇄 삭제의 문제가 발생하는 경우
  위 그림에서 ‘장미란’이라는 학생 정보를 지울 경우 ‘체육관 103’도 함께 삭제되어 다른 튜플들이 ‘체육관 103’을 사용하지 못하는 경우에 발생
  
• 삽입 이상
  튜플을 삽입하는 경우 해당하는 정보가 없어서 Null이 삽입되는 경우
  주소 정보를 함께 삽입하지 않는다면 주소값에 Null이 삽입될 수 있음
  
• 수정 이상
  어떤 값을 참조하는 튜플의 값을 수정할 때 같은 데이터를 참조하는 다른 튜플과 데이터가 달라지는 현상
  위 그림에서 ‘박지성’과 ‘김연아’는 같은 강좌 ‘데이터베이스’를 듣고 있음
  이 때 ‘박지성’의 강의실을 다른 강의실로 수정한다면, 같은 수업임에도 강의실이 다른 문제가 발생할 수 있음
  

이러한 이상현상들은 서로 공유하는 데이터임에도 불구하고 각자의 튜플에 독립적으로 존재하기 때문에 발생
아래와 같이 테이블을 분리한다면 이러한 이상현상들을 해결할 수 있음

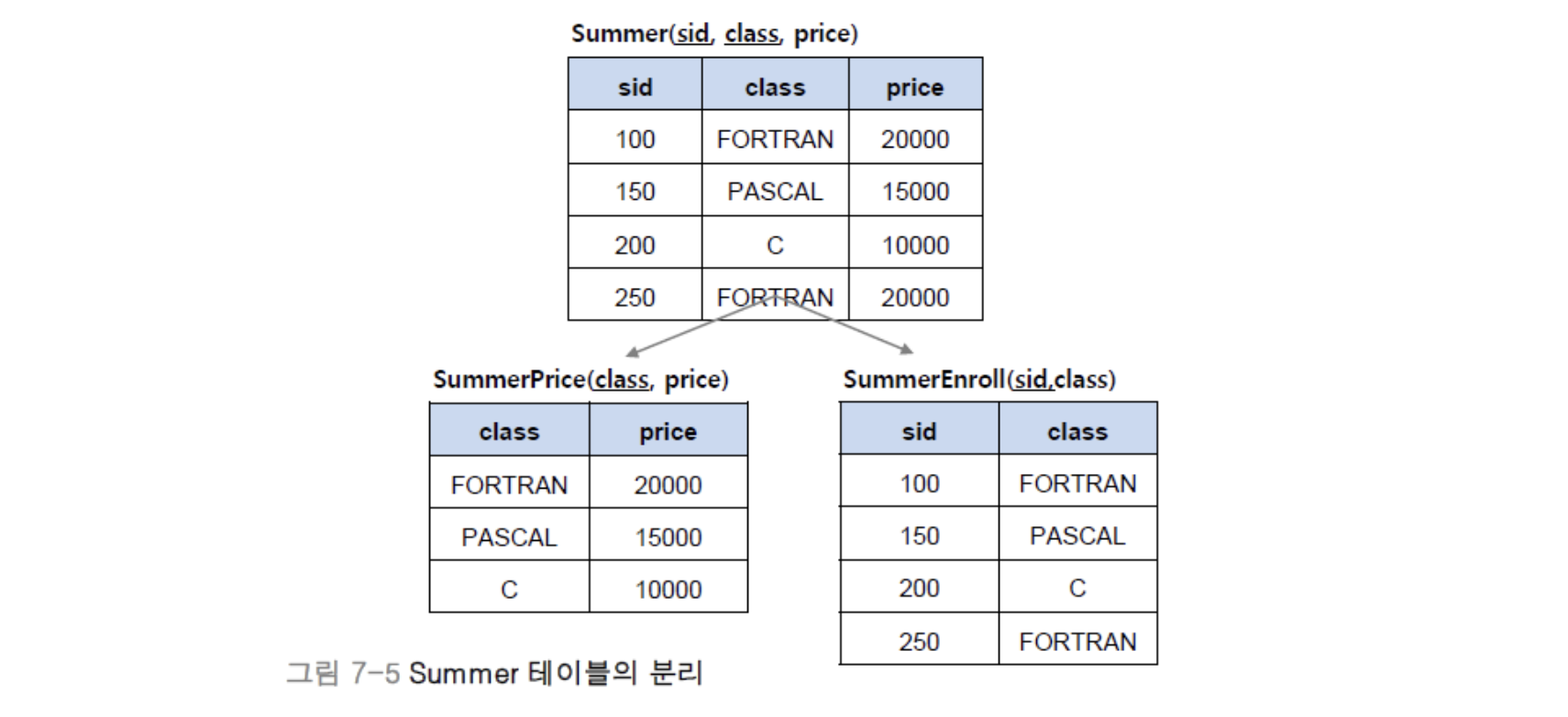
함수 종속성

어떤 속성 A를 알면 다른 속성 B의 값이 유일하게 정해지는 관계
‘A→B’로 표기하며 A를 B의 결정자라고 함

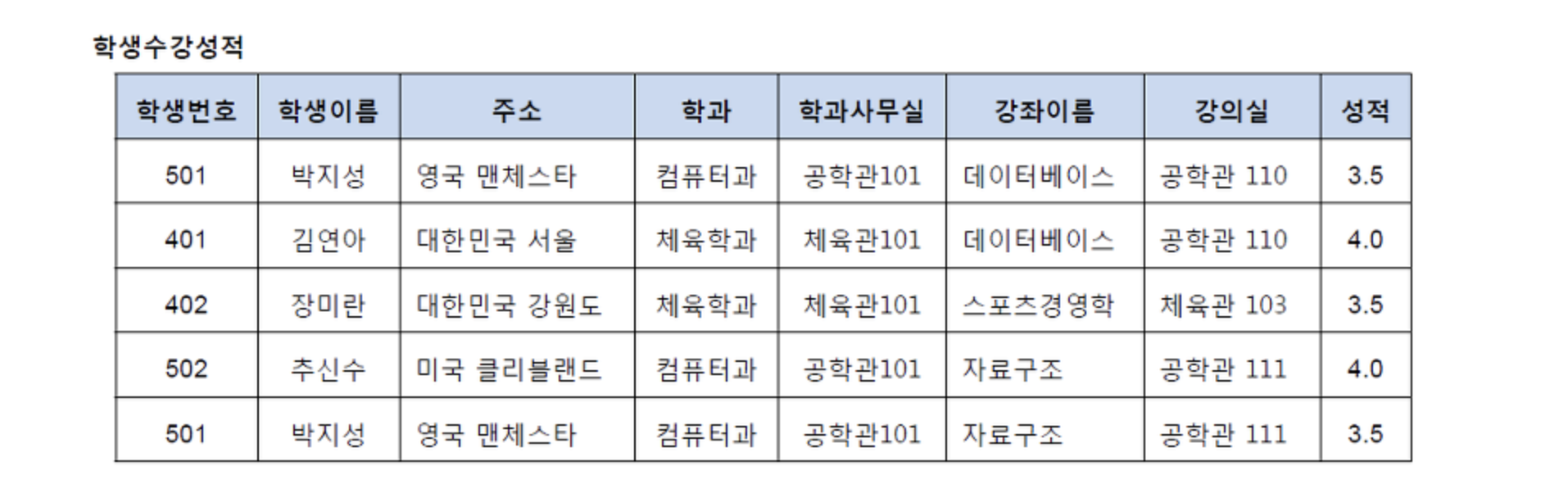
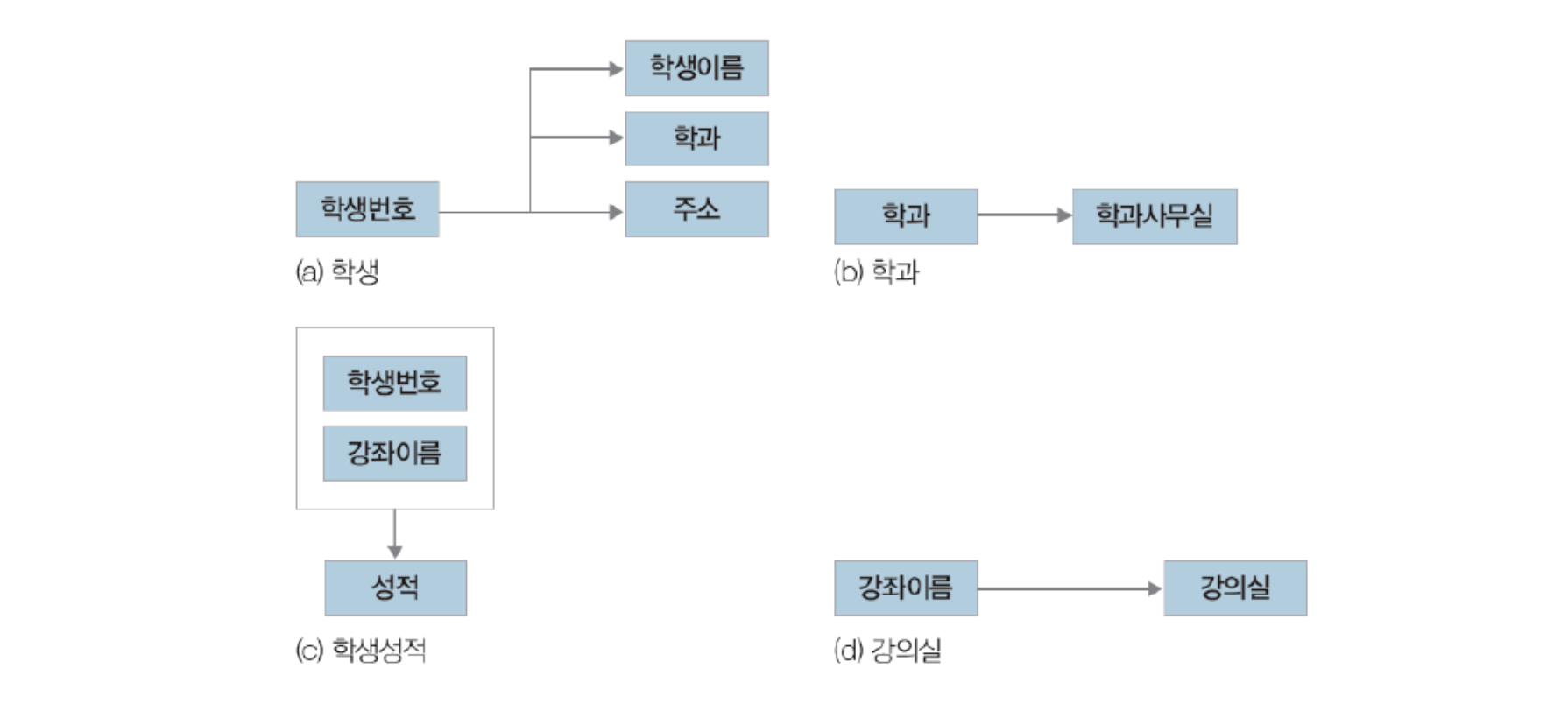
위와 같은 릴레이션에서는 다음과 같은 함수 종속성이 존재함

• 학생번호→학생이름
• 학과→학과사무실
• 강좌이름→강의실

학생이름→학과는 종속되어 보이지만 같은 이름의 다른 학과 학생이 존재할 수 있으므로 종속하지 않음

함수 종속성 규칙

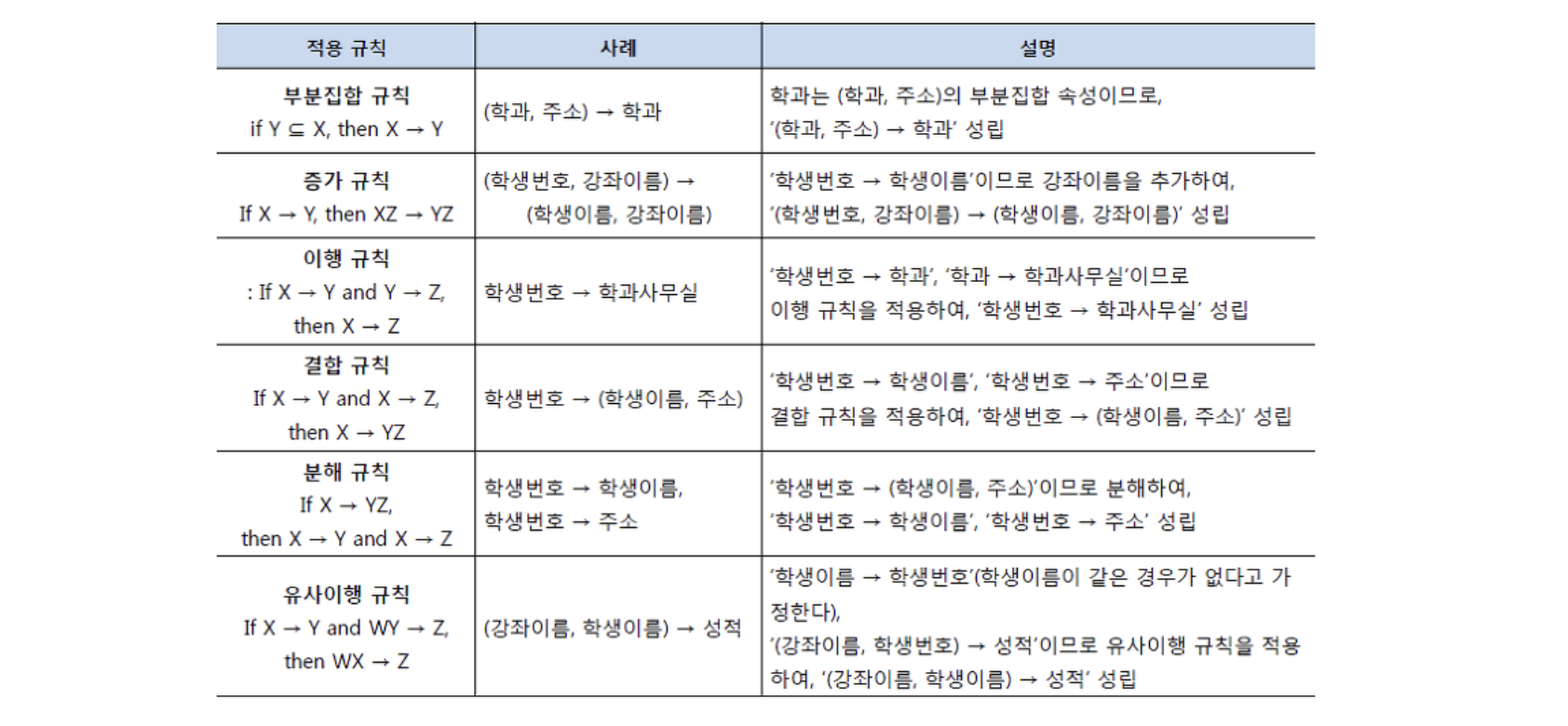
이상현상과 결정자

이상현상은 한 개의 릴레이션에 두 개 이상의 속성이 포함되어 있고, 기본키가 아닌 속성이 결정자일 때 발생
위의 학생수강성적 릴레이션의 경우 기본키를 지닌 학생 정보(학생번호, 학생이름, 주소, 학과)와 기본키가 아니지만 결정자적 성질을 지닌 강좌 정보(강좌이름, 강의실)가 한 릴레이션에 포함되어 있기 때문에 이상현상이 발생한 것
또한 학과, 학생 번호, 강좌 이름은 기본키가 아니면서 결정자이기 때문에 이상현상을 해결하기 위해 총 4개의 릴레이션으로 학생수강성적 릴레이션을 분해하면 됨

정규화

관계형 데이터베이스의 설계에서 중복을 허용하지 않도록 데이터를 구조화하는 프로세스
데이터 중복을 허용하지 않는다면 무결성을 유지할 수 있으며, DB 저장 용량 역시 줄일 수 있음

목표는 이상이 있는 관계를 재구성하여 작고 잘 조직된 관계를 생성하는 것에 있음
크고, 제대로 조직되지 않은 테이블들과 관계들을 작고 잘 조직된 테이블과 관계들로 나누는 것을 포함

목적은 하나의 테이블에서의 데이터의 삽입, 삭제, 변경이 정의된 관계들로 인하여 데이터베이스의 나머지 부분들로 전파되게 하는 것
데이터 삽입, 삭제, 변경 등에서 발생하는 이상현상들을 제거하는 과정이라고도 할 수 있음
정규형이 높을수록 이상현상은 줄어듦

제 1 정규형

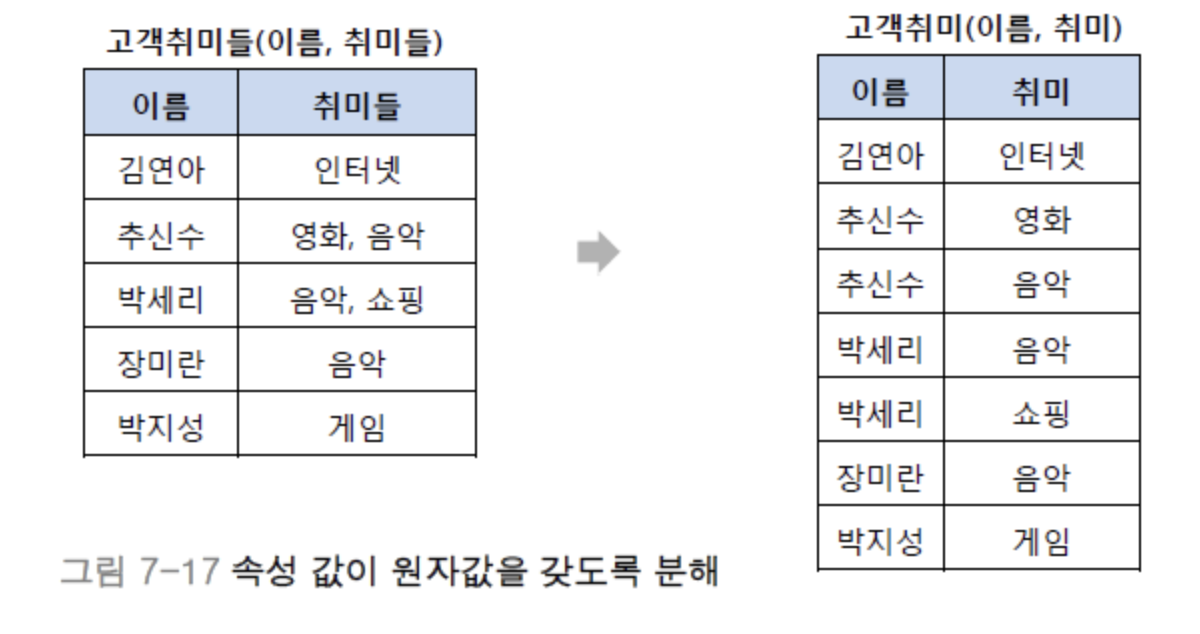
릴레이션의 모든 속성 값이 원자값을 갖는 경우
예를 들어 ‘고객 취미’ 릴레이션에 ‘(추신수, (영화, 음악))’ 이라는 데이터가 있다면 ‘(추신수, 영화), (추신수, 음악)’처럼 분리하는 것이 제 1 정규형

제 2 정규형

릴레이션이 제 1 정규형을 만족하고, 기본키가 아닌 속성이 기본키에 ‘완전 함수 종속’인 경우
완전 함수 종속이란 기본키로 묶인 복합키가 존재할 때 복합키(A,B,C)가 모여서 하나의 다른 값(X)를 결정하고 복합키의 부분집합이 결정자가 되면 안된다는 뜻

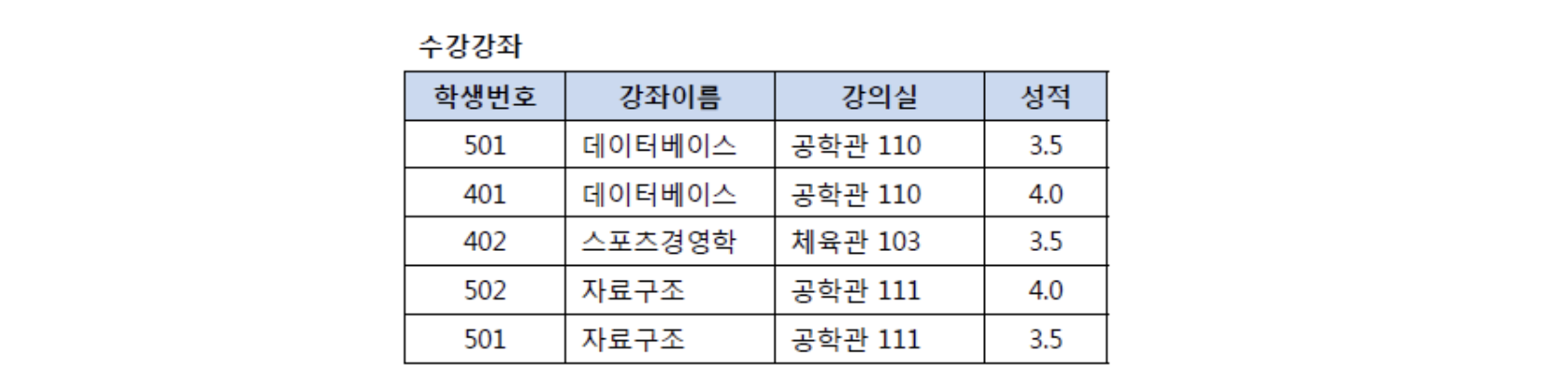
위 수강강좌 릴레이션에서는 ‘(학생번호, 강좌이름)’의 복합키를 가짐
이 복합키로 ‘성적’을 결정하지만, ‘강의실’의 경우 ‘강좌이름’만으로도 결정이 됨
이러한 관계는 ‘부분 함수 종속’

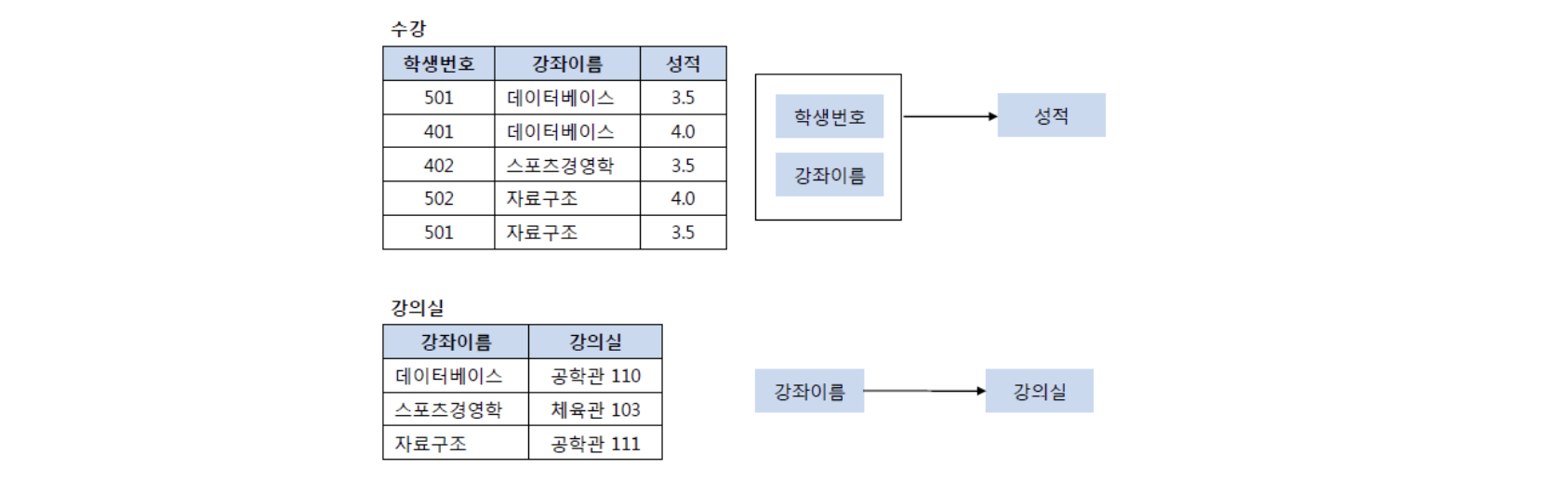
아래와 같이 강좌이름과 강의실을 분리하면 제 2 정규형을 만족함

제 3 정규형

릴레이션이 제2 정규형을 만족하고 기본키가 아닌 속성이 기본키에 비이행적(Non-Transitive)으로 종속하는 경우
이행적 종속이란, A->B, B->C가 성립할 때 A->C가 성립되는 함수 종속성을 의미

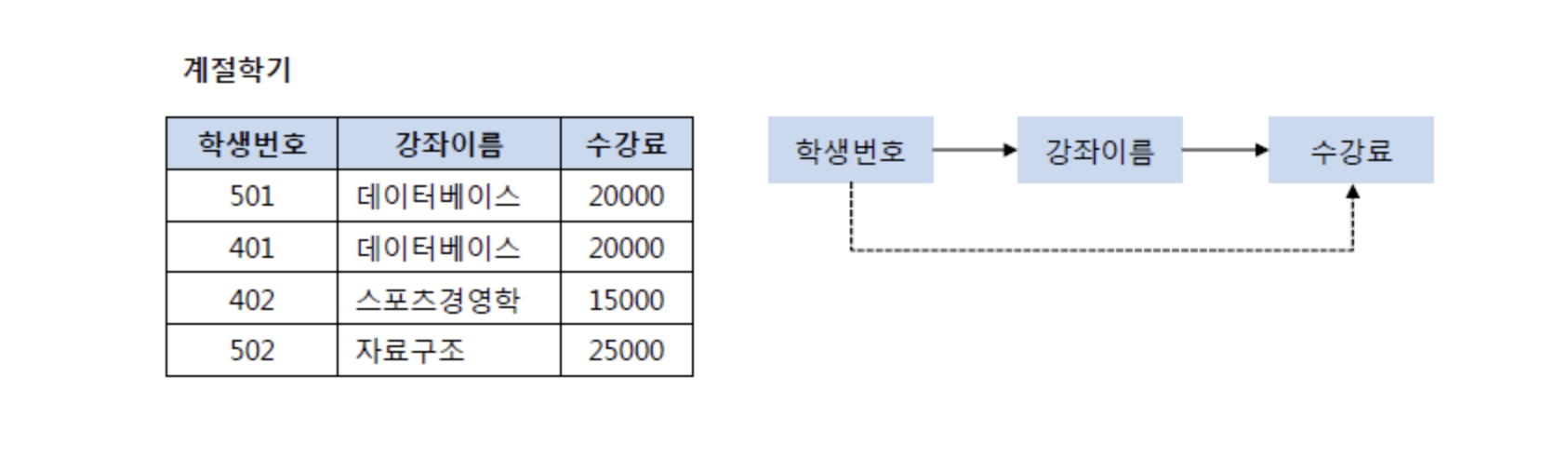
위 릴레이션에서 학생번호 501의 강좌이름이 스포츠경영학으로 변경된다면, 수강료도 15000원으로 변경되어야 함
위 속성들을 독립적으로 만드는 것이 아니라 학생 번호로 학생이 수강하는 강좌이름을 찾게 하고 그 학생번호가 참조하는 강좌이름을 참조하여 수강료를 찾게하여 학생번호가 수강료를 참조할 수 있게 끔 만들면 제3 정규형이 됨

BCNF 정규형

릴레이션 R에서 함수 종속성 X->Y가 성립할 때 모든 결정자 X가 후보키인 경우

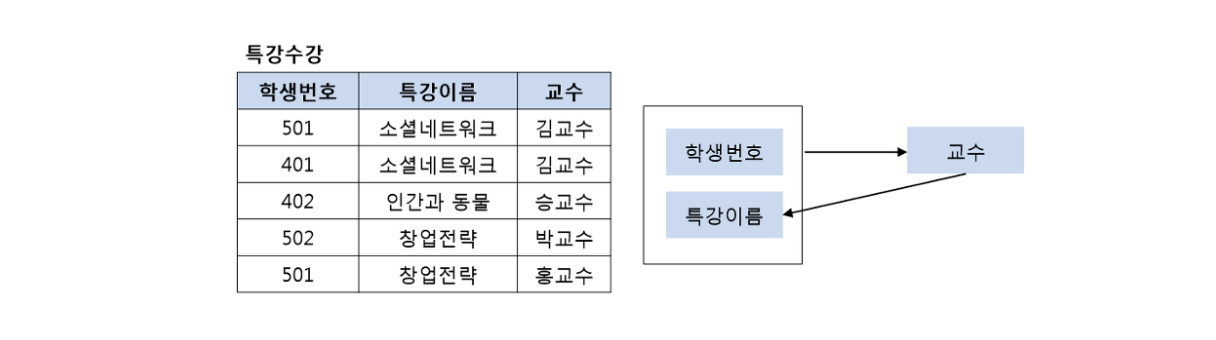
위 ‘특강수강’ 릴레이션에서 기본키는 ‘(학생번호, 특강이름)’이고 교수는 (학생번호, 특강이름)에 완전하게 함수적으로 종속
또한 교수 역시도 특강 이름을 결정하며 결정자의 역할
‘(학생번호, 특강이름)’은 기본키이므로 당연히 결정자이며 후보키
하지만 교수는 결정자이지만 후보키가 아니므로 아래의 왼쪽 테이블은 BCNF 정규형이 아님

아래와 같이 분리하면 BCNF 정규형을 만족함

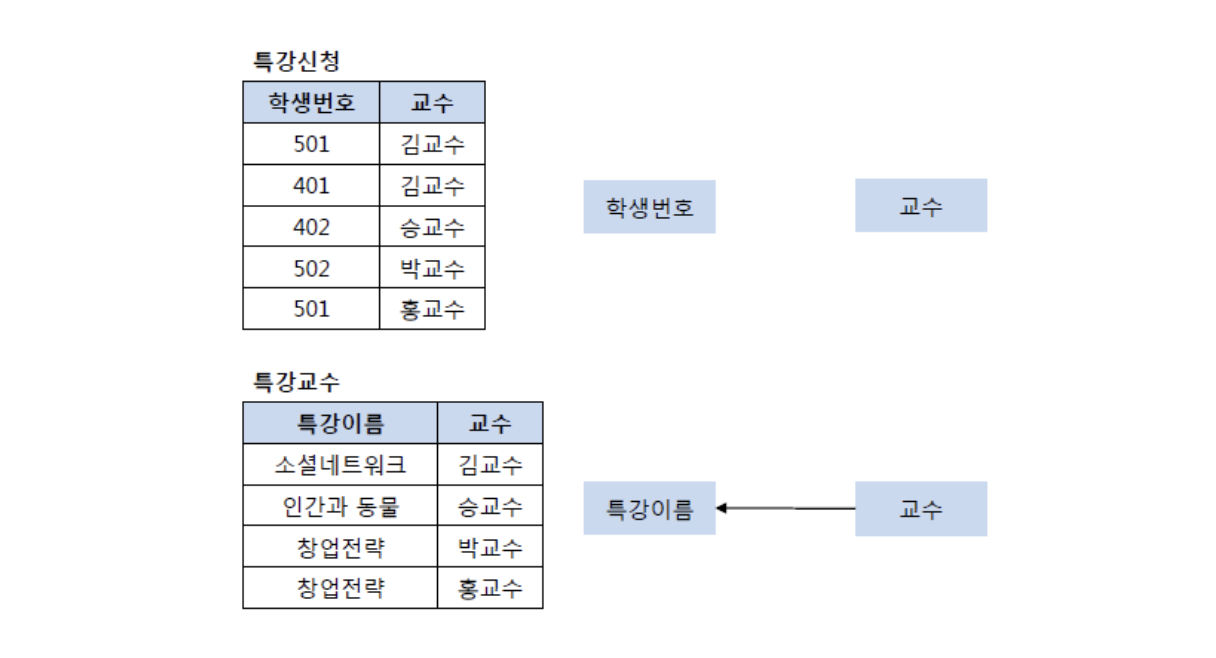
무손실 분해

이상현상을 제거하기 위해서는 위의 자료들처럼 릴레이션을 분리해야 함
하지만 하나의 릴레이션 R을 분해할 때 분해 후의 결과와 달라지면 문제가 발생하게 되므로 우리는 손실이 없이 릴레이션을 분해해야 함

릴레이션 R을 R1과 R2로 분해할 때, R1▷◁R2의 결과가 R로 돌아오기를 만족하는 경우를 무손실 분해라고 함
그리고 R1과 R2는 R1∩R2 -> R1 혹은 R1∩R2 -> R2 중 하나를 만족해야 함
바로 위 예시에서는 ‘교수’를 기준으로 분리했었음
이 때 분리된 릴레이션을 다시 조인한다면 원래의 릴레이션으로 돌아올 수 있음

그러나 아래처럼 ‘특강이름’을 기준으로 분리한다면 조인을 한다고 해도 원래의 릴레이션이 되지 않음

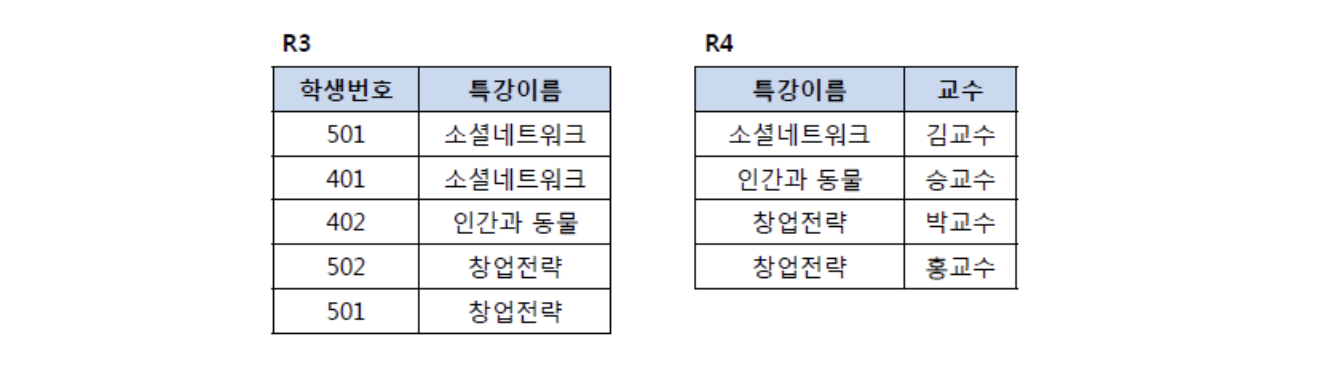
대부분의 릴레이션에서는 BCNF까지 정규화하면 실제적인 이상현상이 없어지기 때문에 BCNF 까지 정규화를 한다고 함