1. 메소드

---

1.1. 메소드 개념

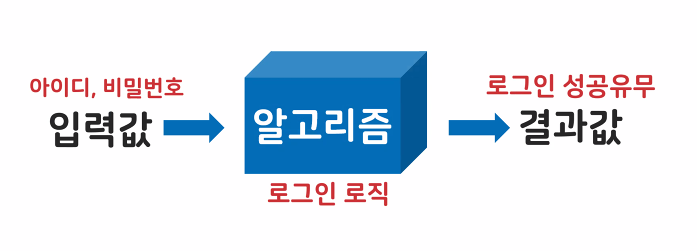
• 메소드를 함수 f(x)로 비유할 수 있다.

• 사용할때 입력 값에 따라 결과 값이 달라진다.

• 입력값 -> 알고리즘 -> 결과값
  

• 소괄호 쓰는 거면 왠만하면 메소드다
  ex) println() 등

1.1.1. 메소드 란?

• 어떤한 작업을 수행하기 위한 명령문의 집합 여러줄의 코드를 하나로 묶어서 표현한 형태
  

1.1.2. 메소드의 기본 구조

• 오류 내용에 >> 파라메터, 아규먼트 이면 메소드에 문제가 생겼을 확률이 높음!
• 같은 저장공간에 있어야 메소드를 사용할 수 있다.
  예) static main의 경우 메소드를 사용하려면 static 메소드로 설정해야 한다.

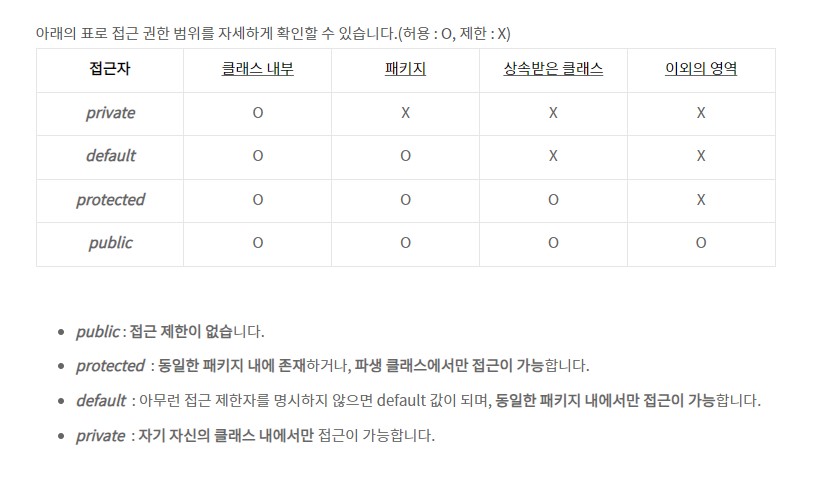
• 접근 제한자 관련 url : 링크

---

1.2. 기초연습

	public static void main(String[] args) {
		// 메소드 사용하기(main 안쪽 영역에서 사용하기)
		double resultMain = addDouble(3.14, 4.2);
		// 메소드 결과(두 수를 더하는 메소드 결과) 출력함.
		System.out.println("첫 번째 실습 메소드 계산결과 : " + resultMain);

		
		int sum = subNum(5,10);
		// 메소드 결과(두 수 중 큰 수에서 작은 값을 빼는 메소드 결과) 출력함.
		System.out.println("두 번째 실습 메소드 계산결과 : " + sum);
		
	}

	// 메소드 생성(main 영역을 벗어나서 작성)
	// 1. 더하기
	// 리턴 타입 : double / 메소드명 : addDouble / 매개변수 : double 2개
	public static double addDouble(double n1, double n2) {

		double result = n1 + n2;
		return result;
	}
	
	// 2.빼기
	// 리턴타입 : int / 메소드명 : subNum / 매개변수 : int 2개
	// 매개변수로 받아온 데이터 2개를 뺀 결과값을 돌려주는 메소드
	// 단, 큰 수에서 작은 수를 뺀 결과값을 돌려주기
	public static int subNum(int n1, int n2) {
		int result = 0;
	
		if(n1 > n2) {
			result = n1 - n2;
		} else {
			result = n2 - n1;
		}
		return result;
	}

---

2. 메소드 오버로딩

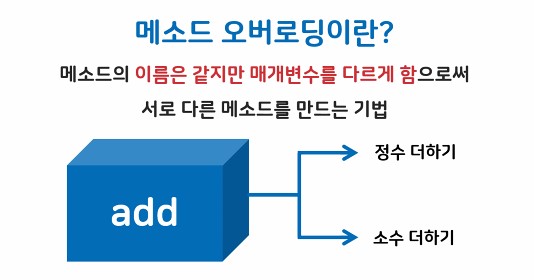
• 메소드의 이름은 같지만 매개변수를 다르게 함으로써 서로 다른 메소드를 만드는 기법 (중복정의!)

---

• 메소드 오버로딩 성립 조건
  1. 메서드의 중복정의는 이름이 같아야 한다.
  2. 매개변수의 갯수 또는 자료형(데이터 타입)이 달라야 한다.
  3. 매개변수와 메소드의 이름이 동일하고 리턴 타입만 다른 경우 오버로딩이 아니다.

// 오버로딩 해보기 실습
	public static void main(String[] args) {

		// 메소드 오버로딩(오버로딩 책 209p 참조)
		// 매개변수의 개수를 다르게 하고, 메소드의 이름을 똑같이 부여
		System.out.println(add(3.5, 5.5));
		System.out.println(add(3, 5));
	}
	
    
	// 메소드 생성하기
    // 메소드 오버로딩 성립 조건
	// 1. 메서드의 중복정의는 이름이 같아야 한다.
	// 2. 매개변수의 갯수 또는 자료형(데이터 타입)이 달라야 한다.
	// 3. 매개변수와 메소드의 이름이 동일하고 리턴 타입만 다른 경우 오버로딩이 아니다.
    
	// 실수 데이터 2개를 입력 받아서 더해주는 메소드
	private static double add(double num1, double num2) {
		// 리턴에 계산 수식을 입력하여 리턴 전달 가능
		return num1 + num2 ;
	}
	
	// 정수 데이터 2개를 입력 받아서 더해주는 메소드
	private static int add(int num1, int num2) {
		// 리턴에 계산 수식을 입력하여 리턴 전달 가능
		return num1 + num2;
	}

메소드 오버로딩 이후 add를 입력하면 2가지 타입의 메소드가 나옴.

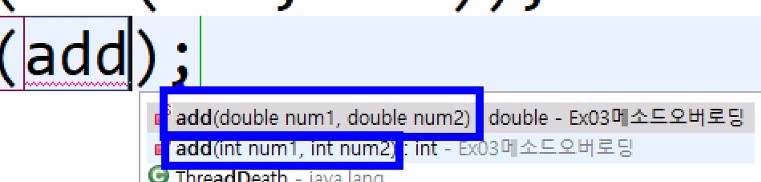
문제 풀어보기

	/*
	* 메소드 예제 - 10에 더 가까운 수 구하기 1. 정수형 num1과 num2를 입력 받으세요. 2. num1과 num2중 10에 더 가까운
	* 수를 반환하는 close10 매소드를 생성하세요.
	*/

		Scanner sc = new Scanner(System.in);
		System.out.print("정수 입력 : ");
		int num1 = sc.nextInt();
		System.out.print("정수 입력 : ");
		int num2 = sc.nextInt();
		int result = close10(num1, num2);
		System.out.println("10에 가까운 수 : " + result);
	}

	public static int close10(int num1, int num2) {

		// 내가 작성한 코드 방법
		int check = 0;
		int n01 = 0;
		int n02 = 0;

		n01 = num1 > 10 ? num1 - 10 : num1;
		n02 = num2 > 10 ? num2 - 10 : num2;

		if(n01+n02 > 0) {
			if (n01 == n02) {
				total = 0;
			} else if (n01 > n02) {
				total = num1;
			} else {
				total = num2;
			}
			
		} else {
			if (n01 == n02) {
				total = 0;
			} else if (n01 < n02) {
				total = num2;
			} else {
				total = num1;
			}
		}

		// 문제 풀어 생각해보기 !
//		5와 9를 봤을 때 10에 더 가까운 수는?
//		10-5=5 / 10-9=1  ---> 더 작은 수가 10에 가깝다고 판단!
//		11, 15
//		10-11=-1/10-15=-5 --> 더 작은 수가 10에 가깝다고 판단XXX
//		-1, -5에서 -를 뺄 수 있는 방법은?
			// 1) 큰 수에서 작은 수를 뺀다. (if 많아진다!)
		
		
		
		// 2) 제곱만드는 법 : -1*-1 = 1 / -5*-5 = 25
		if ( (10-num1)*(10-num1) < (10-num2)*(10-num2) ) {
			check = num1;
		} else if( (10-num1)*(10-num1) > (10-num2)*(10-num2) )  {
			check = num2;
		} else {
			check = 0;
		}
		
		
		// 3) 절대값 : 수직선 위에서 원점으로 부터 어떤 수를 나타내는 점까지의 거리
		if ( Math.abs(10-num1) < Math.abs(10-num2) ) {
			check = num1;
		} else if ( Math.abs(10-num1) > Math.abs(10-num2) ) {
			check = num2;
		} else {
			check = 0;
		}
		return check;
	}

( 완전수 )
예) 6 -> 6의 약수(본인 제외) 1, 2, 3
나머지들을 더하면 본인의 값이 나옴 6 !

	/*
	* 메소드 예제 - 완전 수 구하기
	* 
	*  1.num2가 num1의 약수인지 확인하여 약수라면 true ,  
	*   아니라면 false를 반환하는 isDivisor 메소드를 만들어주세요.
	*/
		
		Scanner sc = new Scanner(System.in);
		System.out.print("num1 입력 : ");
		int num1 = sc.nextInt();
		System.out.print("num2 입력 : ");
		int num2 = sc.nextInt();
		boolean divisor = isDivisor(num1, num2);
		System.out.println(divisor);
		System.out.println(getSum(6));
	
	}

	
	private static int getSum(int num) {
		int total = 0;
		for (int i = 1; i < num; i++) {
			if(num % i == 0) {
				total = total + i;
			}
		}
		return total;
	}

	
	private static boolean isDivisor(int num1, int num2) {
		boolean result = false;
		
//		int[] array = new int[num1];
//		
//		for (int i = 1; i < array.length; i++) {
//			if(num1 % i == 0) {
//				array[i] = i;
//			}
//			if (array[i] == num2) {
//				result = true;
//			}
//		}
		
		// 선생님 풀이 방식
		if (num1 % num2 == 0) {
			result = true;
		}
		return result;
	}

---

3. retuen 타입이 필요없는 void

/* main 영역 */
	public static void main(String[] args) {
		// 메소드 호출
		printFinish();
	}
	
    
/* 메소드 영역 */
	// 완전수 구하기 완료! 를 출력하는 메소드
	public static void printFinish() {
		// void : 리턴 타입이 없을을 의미하는 키워드(리턴 타입이 확정되지 않았을때)
		System.out.println("완전수 구하기 완료!!");
	}

---

그외. 단축키
import 단축키 : 컨트롤 + 시프트 + 알파벳 o