인공지능 되돌아보기

songmin jeon·2024년 4월 5일

클라우드기반 인공지능서비스 엔지니어링과정

목록 보기

129/138

딥러닝 개념

- 딥러닝이란 뭘까?

1) 인공지능

인간이 가지는 지적 능력들을 컴퓨터를 통해 구현하는 기술들의 집합
기술 자체를 총칭하는 개념 -> 형태 자체가 없는 포괄적 개념이다.

2) 머신러닝

데이터를 기반으로 컴퓨터 스스로 규칙을 찾아 학습하는 기술
인공지능을 구현하기 위한 핵심 기술이 머신러닝이다.

3) 딥러닝

인간의 신경망을 모방하여 학습하는 기술
머신러닝에 포함된 세부적 기술
-> 머신러닝이 할 수 없는 것들을 해결해주는 기술

가) 머신러닝이 학습을 할때 사용하는 데이터를 살펴보자!

정형데이터 : 표의 형태를 가지고 있음
-> DataFrame / ndarray

나) 딥러닝이 학습을 할때 사용하는 데이터를 살펴보자!

유방암 데이터(ndarray), 폐암 데이터(ndarray)
보스턴 집값(CSV파일), 개고양이 분류(img), 네이버 감성분석(텍스트 데이터), 로이터 뉴스(텍스트 데이터), 패션데이터(img), 아기울음소리/섬집아기/자장가(음성데이터)
딥러닝의 구조
- 딥러닝은 어떤 요소들로 구성이 되어 있을까?
-> 딥러닝 모델은 사람의 신경망을 모방해서 만들었다

1) 뉴런 : 신경계를 구성하는 세포, 전기 신호를 전달
-> 생각/반응/행동

사람의 뉴런은 신경세포, 인공신경망에서 뉴런은 선형회귀(y=wx+b)

2) 퍼셉트론 : 기존 뉴런은 모든 신호를 다음 뉴런으로 전달해주는 구조 사람의 신경망은 역치라는 문턱 값을 가지고 있음.

신호 강도 > 역치(문턱값) : 다음 뉴런으로 신호 전달
신호 강도 < 역치(문턱값) : 신호 전달 X
인공신경망도 사람의 신경망과 최대한 유사하게 역치를 구현
역치를 구현하기 위해 뉴런에 활성화 함수를 연결시켜 역치 구현 뉴런 + 활성화 함수 = 퍼셈트론

3) 다중 퍼셉트론 :

기존 퍼셉트론
-> 인간의 신경망을 모방 -> 문제 해결능력 뛰어남
-> 논리게이트 XOR문제 해결 x
-> 인공지능의 첫번째 겨울(연구 동결)
-> 문제 해결을 위해 퍼셉트론(하나의 직선)을 여러 층으로 쌓아서 다층 퍼셉트론으로 구성(연산을 여러번 하도록)

- 출력층의 구조

1) 회귀

출력층 뉴런의 갯수 : 1개
손실함수 (loss) : MSE(평균 제곱 오차)
출력층 활성화 함수 : 생략 가능(Linear)
- 뉴런의 구조(형태) -> 선형 회귀 함수
  선형회귀 함수에서 나온 예측값을 활성화 함수를 통과시키지 않고 그대로 출력하면 회귀 예측값이 나온다.

2) 분류

2-1) 이진 분류
- 출력층 뉴런의 갯수 : 1개
- 손실함수 (loss) : Binary_crossentropy
- 출력층 활성화 함수 : Sigmoid

Sigmoid : 0~1 사이의 확률 정보를 예측해서 예측값이 0.5보다 크거나 같으면 1로 예측, 작으면 0으로 예측

2-2) 다중 분류
- 출력층 뉴런의 갯수 : 원핫 인코딩한 정답 데이터의 컬럼 갯수
- 손실함수 (loss) : categorical_crossentropy
- 출력층 활성화 함수 : Softmax

Softmax : 다중 분류에서 각 퍼셉트론의 예측 확률합을 1로 설정
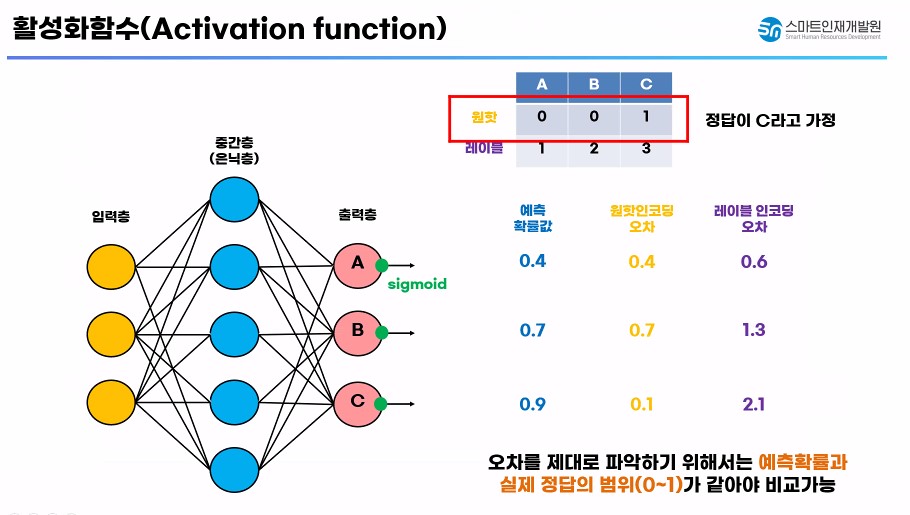
기존 Sigmoid 함수 -> 이진 분류에 특화가 되어 있다.(0/1)
실제 정답의 범위(0~1)와 예측 확률이 같아야 비교가 가능하다.
시그모이드 함수의 다중분류에서 오차 파악이 제대로 되지 않는다.
다중 분류에서 오차파악 / 예측확률을 정확하게 알아보기 위해 Softmax 사용

- 오차 역전파(중요)

신경망이 학습되는 원리는 무엇일까?
역으로 가중치를 수정하면서 신경망의 성능 개선
- 순전파 : 입력 데이터를 입력층에서부터 출력층까지 정 방향으로 이동시키면서 출력 값을 예측해나가는 과정(예측)
- 역전파 : 출력층에서 예측값이 예측됨과 동시에 에러값(오차) 발생. 에러 값을 중간층을 통해 입력층 쪽으로 전파시키면서 가중치를 업데이트 하는 과정 - 경사 하강법을 이용해서 오차 값을 낮춰준다.(학습)

1 epochs 에서 일어나는 프로세스 : 데이터 입력 -> 순전파(예측) > 역전파(학습) - 신경망의 학습을 위해서는 경사하강법(손실함수(loss의 미분))을 사용

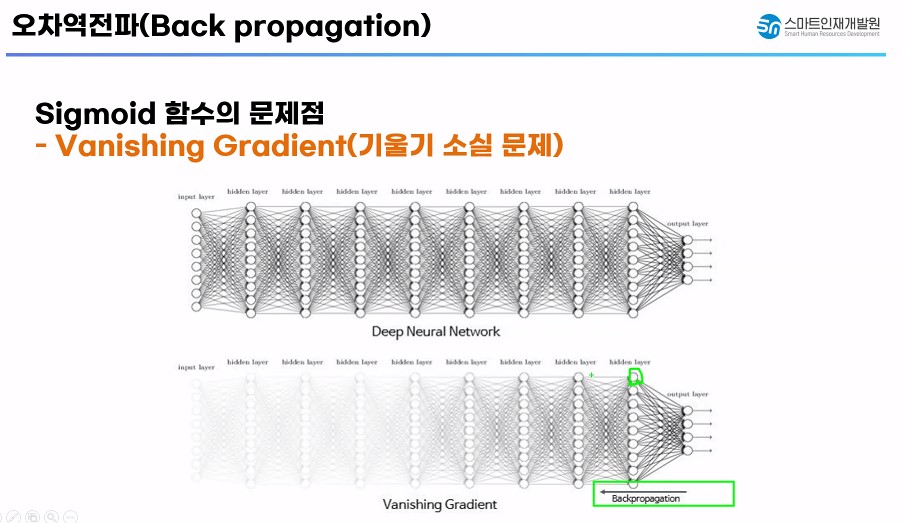
오차 역전파에서 문제점 발생
- 초기 활성화 함수의 종류 : 계단함수 -> Sigmoid 함수
- Sigmoid 함수를 사용한 신경망에서 경사하강법을 적용/성능개선
- 기울기 소실 문제가 발생 : 오차 역전파를 통해 경사 하강법으로 성능을 개선 시킬때 Sigmoid 함수의 미분 최대값이 0.25
  
  -> 컴퓨터가 기울기를 인식하기 못하는 문제가 생겼다!
  -> 컴퓨터가 학습하는 방법 : 순간적인 기울기를 구해서 기울기가 0이 되는 지점의 가중치를 찾아가는 방법으로 학습
  -> 기울기를 감지하지 못한다면? : 학습을 진행하지 못하는 문제가 발생(성능개선 X)
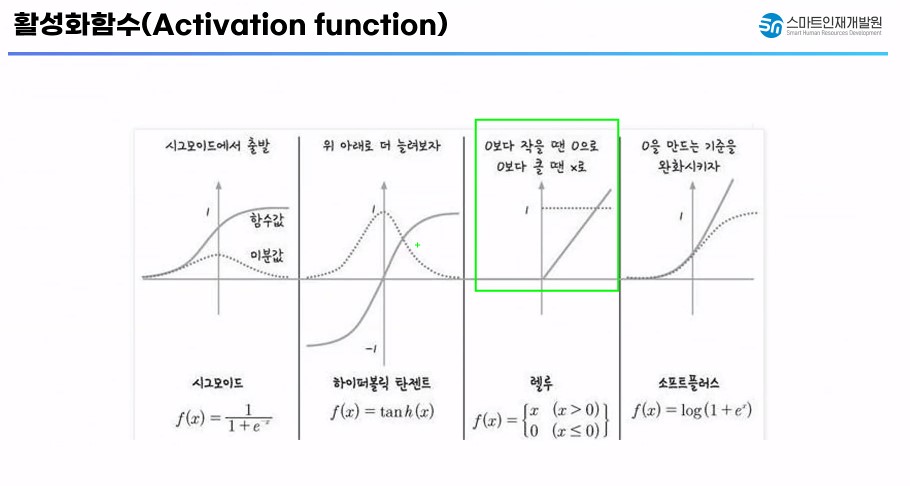
기울기 소실문제를 해결하기 위해 Sigmoid 함수의 대체 함수를 찾아보자.

tanh : 하이퍼볼릭 탄젠트(tanh)
-> 위 아래로 범위를 늘려줘보자/ (Sigmoid 함수의 범위 0~1)
-> 함수의 범위를 늘려서 기울기 소실문제에서 잘 버티지만 결국 형태는 Sigmoid함수와 동일 - 결국 기울기 소실 문제에서 자유로울 수는 없다.

relu

0보다 작을 때는 값을 0으로 / 0보다 크면 그값을 그대로 사용
기울기 소실 문제를 해결
가장 기초적으로 많이 사용하는 활성화 함수

Leaky ReLU / ELU

ReLU 함수의 파생 함수

- 최적화 함수

신경망을 좀 더 효과적으로 학습 시키는 경사하강법을 찾아봅시다.

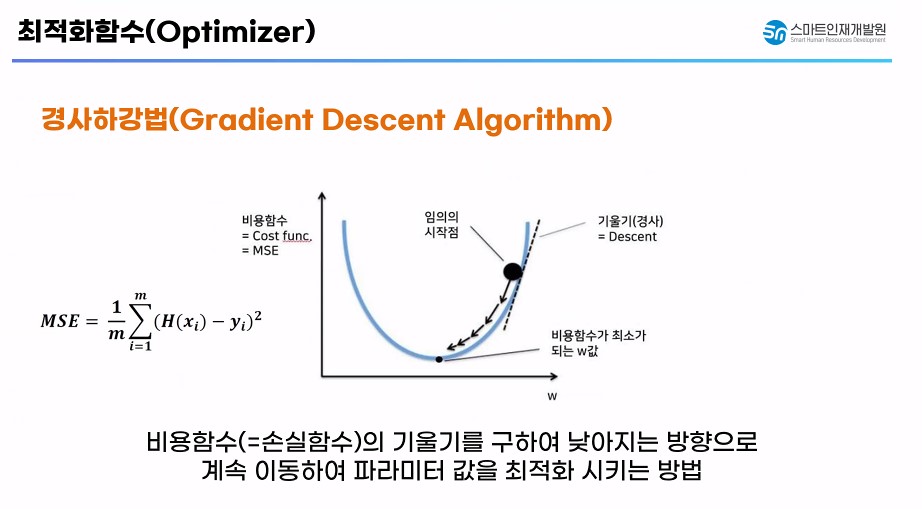
1) 경사하강법

비용함수(손실함수, loss)의 기울기를 구해서 기울기가 낮아지는 방향으로 가중치를 이동시키면서 파라미터 값을 최적화 시키는 방법

2) 확률적 경사하강법

모든 데이터를 연산하는 경사하강법은 컴퓨팅 자원 소모가 높고, 속도가 느리다 -> 단점
일부 데이터만 가지고 경사하강법을 진행해서 자원과 속도를 확보

3) 미니배치 확률적 경사하강법

일반적으로 PC 메모리의 한계 및 속도 저하 때문에 대부분의 경우에는 한 epochs에 모든 데이터를 집어 넣기 힘들다.
일반 경사하강법과 확률적 경사하강법의 절충안
데이터를 미니배치로 나눠서 배치별로 경사하강법을 진행

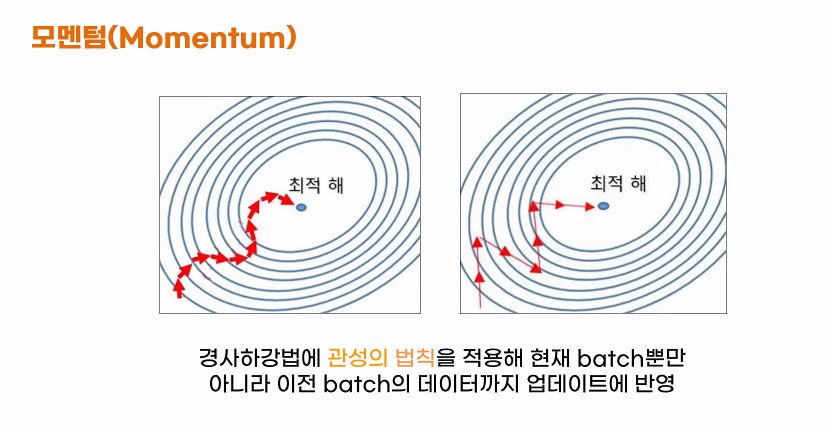
4) Momentrm(모멘텀)

경사하강법에 관성의 법칙을 적용해서 현재 batch뿐만 아니라 이전 batch에 데이터까지 업데이트에 반영합시다!
가중치를 수정하기 전 이전 학습 데이터 방향까지 참고해서 업데이트를 진행!
경사하강법이 진행되면서 가중치가 잘 업데이트 되었다면 해당 방향으로 더 많이 업데이트
아니라면 방향을 틀어 최적 값에 맞게 유연하게 수정하는 방식

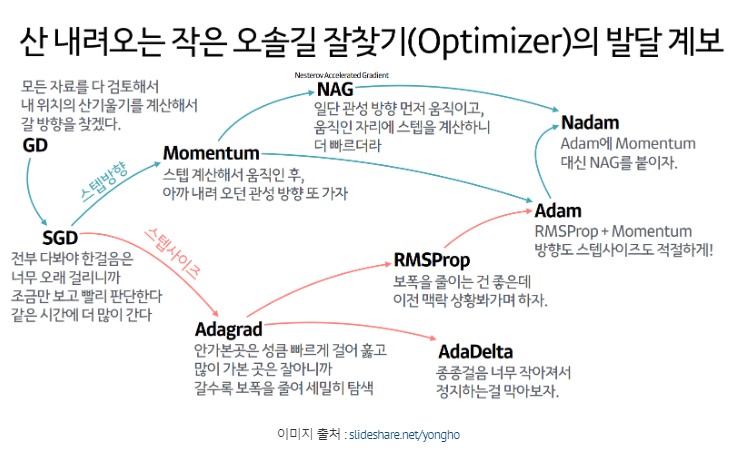
5) 네스테로프 모멘텀(NAG) -> 스탭 방향

모멘텀을 개선한 방식
-> 모멘텀 : 여러가지 방향으로 최적 가중치 거리를 계산한 후 최적 값으로 이동
-> 미리 해당방향으로 이동한다(가정) -> 값을 계산하고 -> 실제 업데이트에 반영
-> 불필요한 이동을 더 줄일 수 있다.

6) Adagrad(아다그라드) -> 스탭 사이즈

가중치를 업데이트 하면서 학습률을 점차 감소시키는 방식
처음에는 크게 학습하다가 점차 조금씩 학습 시키는 방식
학습을 빠르고 정확하게 할 수 있음.

7) RMSProp -> 스탭 사이즈

Adagrad 단점을 해결하기 위해 등장한 최적화 함수
Adagrad : 최적해를 찾기 전에 스탭 사이즈가 줄어서 더이상 최적해를 못 찾는 문제발생
지수 이동 평균을 도입해서 최적해를 끝까지 찾아가도록 만들어준 최적화 함수
지수 이동 평균 : 과거에 모든 기간을 계산 대상으로 놓고 최근 데이터에 더 놓은 가중치를 두는 가중 이동 평균법

8) Adam

RMSProp + Momentum
스탭의 사이즈와 방향 둘다 고려해서 최적해를 찾아가자.
최적해를 찾아가기 위해 스텝 사이즈도 적절하게 조절하고 방향도 알맞게 잡아줍시다.
현재 가장 많이 사용하는 최적화 함수다 !

지금까지 살펴본 신경망은 MLP

- CNN(Convolutional Neuran Network, 합성 곱 신경망)

왜? 합성 곱 신경망을 도입하게 되었을까?
- 신경망은 여러 정형/비정형 데이터 모두 사용 가능하다.
- MLP(다층퍼셉트론) -> 이미지를 처리할때 픽셀 단위로 학습과 예측을 진행, MLP의 경우 이미지 픽셀의 위치에 민감하게 동작. 같은 이미지라도 사이즈가 위치가 달라지면 예측을 정확하게 못함
MLP의 픽셀 위치에 민감하게 동작하는 부분을 개선 시켜서 이미지에서 특징을 추출해서 비교(CNN 작동 방식)
CNN의 구조
특징 추출부(Feature Extractor) + 분류기(Classifier)
특징 추출부 = Conv Layer + Pooling Layer
- Conv Layer : 돋보기 - 이미지에서 중요한 특성을 더 확대시키고 도드라지게 만들어 주는 층
- Pooling Layer : 중요한 특성은 남기고 나머지 특성들을 제외시키는 층
어떻게 특징을 추출할까?
- 입력된 이미지에서 특징을 추출할 수 있는 가중치들이 들어 있는 필터 개념 도입
- 이미지 전체 영역에 대해 일괄적으로 필터를 사용하는 것 보다 특정 범위에 한정해서 필터를 적용한다면 훨씬 효과적으로 특징을 추출할 수 있을 것이다. 아이디어에서 착안
- 부분적으로 적용된 필터를 이동시키면서 필터가 적용된 이미지의 일부를 합성 곱 연산을 통해 특징을 추출하는 방식을 사용
- 필터 내부에 들어 있는 값(파라미터)들은 w(가중치)에 해당 한다.

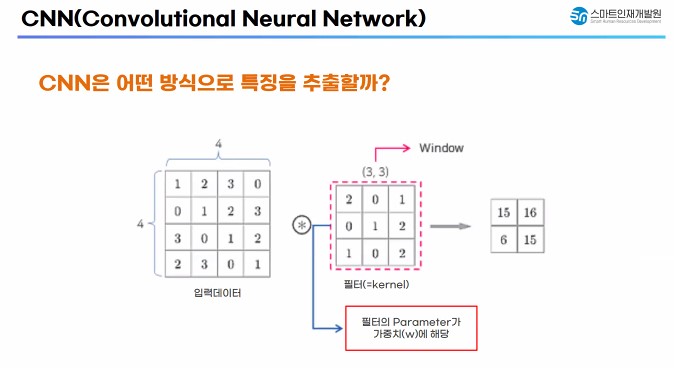
컬러 이미지 합성 곱 연산
- 이미지의 구조
  1) 흑백 이미지 (X, Y, 1(0~255)) -> 합성 곱 연산
  2) 컬러 이미지 (X, Y, 3(RGB 채널))

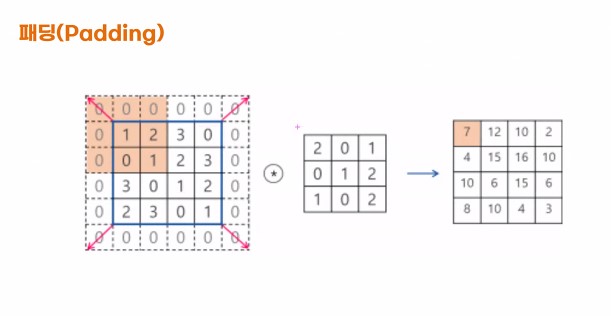
패딩(Padding)
- 필터를 적용할때 마다 이미지의 크기가 줄어드는 효과
- 필터의 크길 인해 가장자리의 데이터가 부족하기 때문에 입력과 출력 이미지의 크기가 바뀌고 가장자리 데이터가 충분한게 학습되지 않느다.
- 이를 보완하기 위해 테두리에 0값을 둘러 채워주는 것을 패딩
  1) Same : 테두리에 0값을 자동으로 채워준다. - 이미지 입출력이 동일하게 유지된다.
  2) Valid : 테두리 사용 안한다.
축소 샘플링
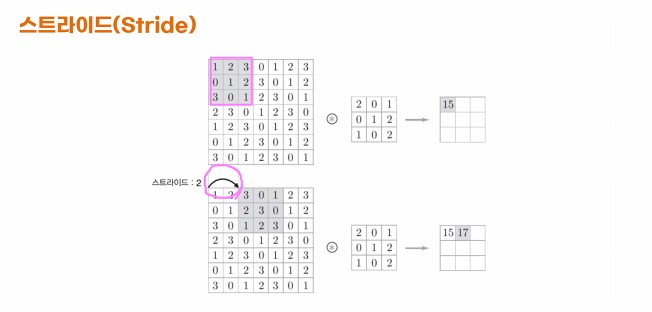
- 스트라이드(Stride)
  - 합성공 연산을 수행할때 필터를 얼마나 이동시킬 것인가?
  - 기본 값은 1픽셀씩 건너 뛰면서 합성곱 연산을 수행하는 방법
  - 스트라이드를 지정해서 2픽셀 / 3픽셀씩 건너 뛰면서 합성곱 연산을 수행하는 방법
- 풀링(Pooling)
  - CNN에서 합성곱 수행 결과를 모두 넘기지 않는다.
  - 일정 범위 내에서 가장 큰 값 / 평균을 넘기는 방법
  - Max Poolong : 설정된 지역내에 가장 큰 값만 넘겨주는 것 - 상대적으로 많이 사용
  - Average Pooling : 설정된 지역 내에 평균 값을 구해서 넘겨주는 것
  - 주의할 점
  - 특정 추출부와 분류기를 연결할때 사이에 Flatten층을 추가
  - 분류로 사용되는 MLP는 1차원 데이터를 받아서 학습
    -> 특성이 추출된 이미지를 1차원으로 퍼주는 작업이 필요함 -> Flatten 층이 1차원 변환

전이학습
- 다른 데이터 셋으로 이미 학습한 모델을 이용해서 유사한 다른 데이터를 인식하는데 사용하는 기법
- 잘 학습된 사람의 지식을 그대로 받아와서 문제 해결을 하는 방식
- 특성 추출 방식
  - CNN의 구조에서 특성 추출부를 이미 학습된 모델로 대체하는 방식
  - 특성추출부만 사용하는 이유는 분류기(MLP)는 우리가 해결하고자 하는 문제에 맞춰서 설정
  - 단 새롭게 분류할 클래스가 사전 학습에 사용된 데이터와 매우 특징이 다르면 특성 추출부의 일부분만 재 사용한다.(미세조정방식)
- 미세 조정 방식
  - 사전 학습된 모델의 가중치를 목적에 맞게 전체 또는 일부를 재학습 시키는 방식
  - 특성 추출부의 층들 중 하단부의 층들 몇개는 분류기(MLP)와 함께 새로 학습을 시키는 방식
  - 처음에는 분류기의 파라미터가 랜덤하게 초기화 되어 있는으므로 특성 추출부의 앞 단계를 학습되지 않도록 동결시키고 뒷 간의 일부 계층만 학습이 가능하게 설정한 후 분류기(MLP)와 함께 학습시켜 파라미터를 적당하게 조절해주는 방식

- RNN

(Recurrent Neural Network, 순간 신경망)

등장 배경
- 순서 있는 데이터 / 시간적 개념이 들어간 시계열 데이터를 해결하기 위해 RNN이 고안
- 문장을 보고 이해한다.(텍스트 데이터) - 각 단어가 정해진 순서대로 입력이 되어야한다는 것
- 과거에 입력된 데이터와 나중에 입력된 데이터 사이의 관계를 고려

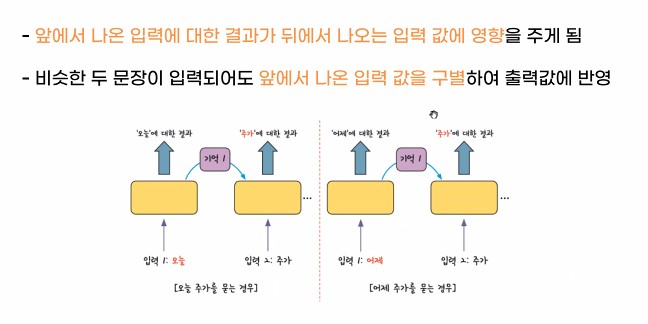
일반 신경망과의 차이점
- RNN은 여러개의 데이터가 순서대로 입력되었을때 앞서 입력 받은 데이터의 연산 결과를 잠시 기억해놓는 방식
- 다음 데이터가 들어오면서 기억된 연산 결과와 함께 연산을 진행하는 방식
- 앞에서 나온 입력에 대한 결과가 뒤에서 나오는 입력 값에 영향을 주는 구조
- 비슷한 두 문장이 입력되어도 앞에서 나온 입력 값을 구별해서 출력 값에 반영을 함.

활용사례(순차기반 데이터를 처리할때 RNN이 효과적이다)
1) 시계열 데이터
2) 음악 데이터 - 음악(재생시간)
3) 문장(텍스트 데이터) 분석
4) 번역

RNN의 단점
- RNN의 기본 활성화 함수 : tanh -> 기울기 소실문제에서 자유롭지 못하다.
  -> 순환 횟수가 늘어날 수록 역전파 진행시 기울기가 점차 줄어들어서 학습을 제대로 못한다.
  -> 시간이 지날수록 이전 과거 데이터를 연산했던 결과값을 잊어버린다.

RNN의 단점을 해결하기 위해 LSTM 등장!
-> 순환 횟수가 많아져도 과거의 데이터를 기억할 수 있는 방안이 필요
-> 데이터를 기억해주는 메모리 셀 -> 기억 공간 추가

메모리셀 : 시간 t, 메모리셀 c
-> 과거에 연산된 데이터부터 현재 시각 t까지 연산된 대부분의 정보 -> c에 저장
-> 별도로 저장 : 오차 역전파를 진행할때 c 메모리 셀은 활성화 함수를 통과하지 않음.
- 미분 했을때 값이 줄어드는 영향을 받지 않는다. -> 기울기 소실 일어나지 않는다.
  -> 데이터를 LSTM 계층 내에서만 주고 받고 다른 층으로는 전달하지 않는다.
- 기울기 소실 문제와 과거 데이터를 잊어버리는 문제를 해결하기 위해 LSTM이 대안으로 등장

- 워드 임베딩

자연어

컴퓨터가 효율적으로 자연어 처리를 하기 위한 방법론
자연어 : 무한대의 가짓수가 나온다 -> 어순/단어조합/맞춤법/유사어

-> 무한대의 조합식이 나오는 자연어를 컴퓨터가 잘 이해할 수 있도록 단순화 토큰화나 인코딩이 아닌 컴퓨터가 쉽게 이해할 수 있도록 변환 시켜주는 것
-> 임베딩은 희소표현(원핫 인코딩) -> 밀집표현(실수형태)로 변환 시켜주는 것을 의미
-> 워드 임베딩은 한 단어의 의미를 풍부하게 만들어주는 역활을 한다.
-> 밀집 표현을 사용했을때 단어들의 유사도(cosine 유사도)까지 판단해서 예측에 반영 가능

코사인 유사도

단어와 단어간의 유사한 정도를 표현하는 방법
범위 : -1 ~ 1
코사인 유사도가 1이다 : 단어가 완전 일치하다.
코사인 유사도가 0이다 : 두 단어가 관계가 없다(독립관계)
코사인 유사도가 -1이다 : 단어가 반대되는 의미를 가지고 있다.
-> 코사인 함수 사잇 각
0도 ~ 180도
사잇 각이 0도인 경우 : 단어가 일치하다(코사인 유사도 : 1)
사잇 각이 90도인 경우 : 두 단어가 관계가 없다(독립적인 관계)
사잇 각이 180도인 경우 : 두 단어가 반대되는 의미를 가지고 있다(코사인 유사도 : -1)

songmin jeon

제가 한 번 해보겠습니다.