문제 설명
머쓱이는 구슬을 친구들에게 나누어주려고 합니다. 구슬은 모두 다르게 생겼습니다. 머쓱이가 갖고 있는 구슬의 개수 balls와 친구들에게 나누어 줄 구슬 개수 share이 매개변수로 주어질 때, balls개의 구슬 중 share개의 구슬을 고르는 가능한 모든 경우의 수를 return 하는 solution 함수를 완성해주세요.
제한사항
1 ≤ balls ≤ 30
1 ≤ share ≤ 30
구슬을 고르는 순서는 고려하지 않습니다.
share ≤ balls
입출력 예
| balls | share | result |
|---|---|---|
| 3 | 2 | 3 |
| 5 | 3 | 10 |
입출력 예 설명
입출력 예 #1
- 서로 다른 구슬 3개 중 2개를 고르는 경우의 수는 3입니다.
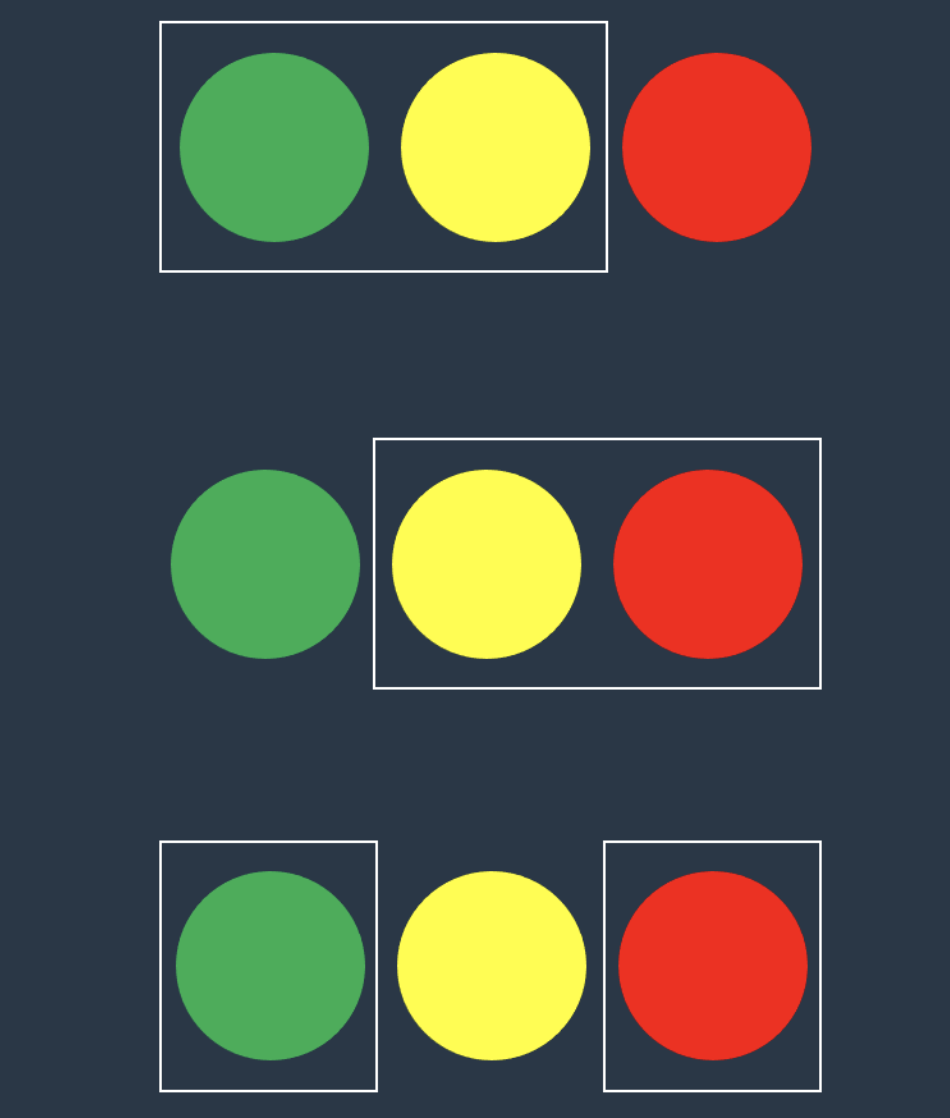
입출력 예 #2
- 서로 다른 구슬 5개 중 3개를 고르는 경우의 수는 10입니다.
Hint
서로 다른 n개 중 m개를 뽑는 경우의 수 공식은 다음과 같습니다.
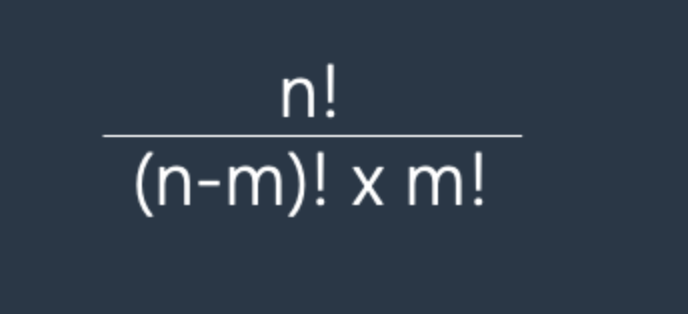
내 풀이: 첫번째 시도
class Solution {
public int solution(int balls, int share) {
int answer = 0;
int n = 1;
int m = 1;
if(balls == share) {
answer=1;
} else {
for(int i=0; i<=balls-share-1; i++){
n*=(balls-i);
}
for(int i=balls-share; i>=1; i--) {
m*=i;
}
answer = n/m;
}
return answer;
}
}생각을 해봤을 때 분자인 n!은 (n-m)! 혹은 m!을 이미 가지고 있을 것이다. 따라서 나는 분자인 int n을 n!에서 m! 을 제거하고 그 다음 분모인 int m을 그냥 (n-m)!을 가지고 가기로했다.
(지금 생각해보니 (n-m)!을 빼고 m!을 분모로 갖는게 런타임이 조금 더 빨랐으려나 싶음...)
여튼, 내가 기존에있던 테스트케이스인 balls=5, share=3과 생성한 테스트케이스인 balls=7, share=3과 함께 해보면
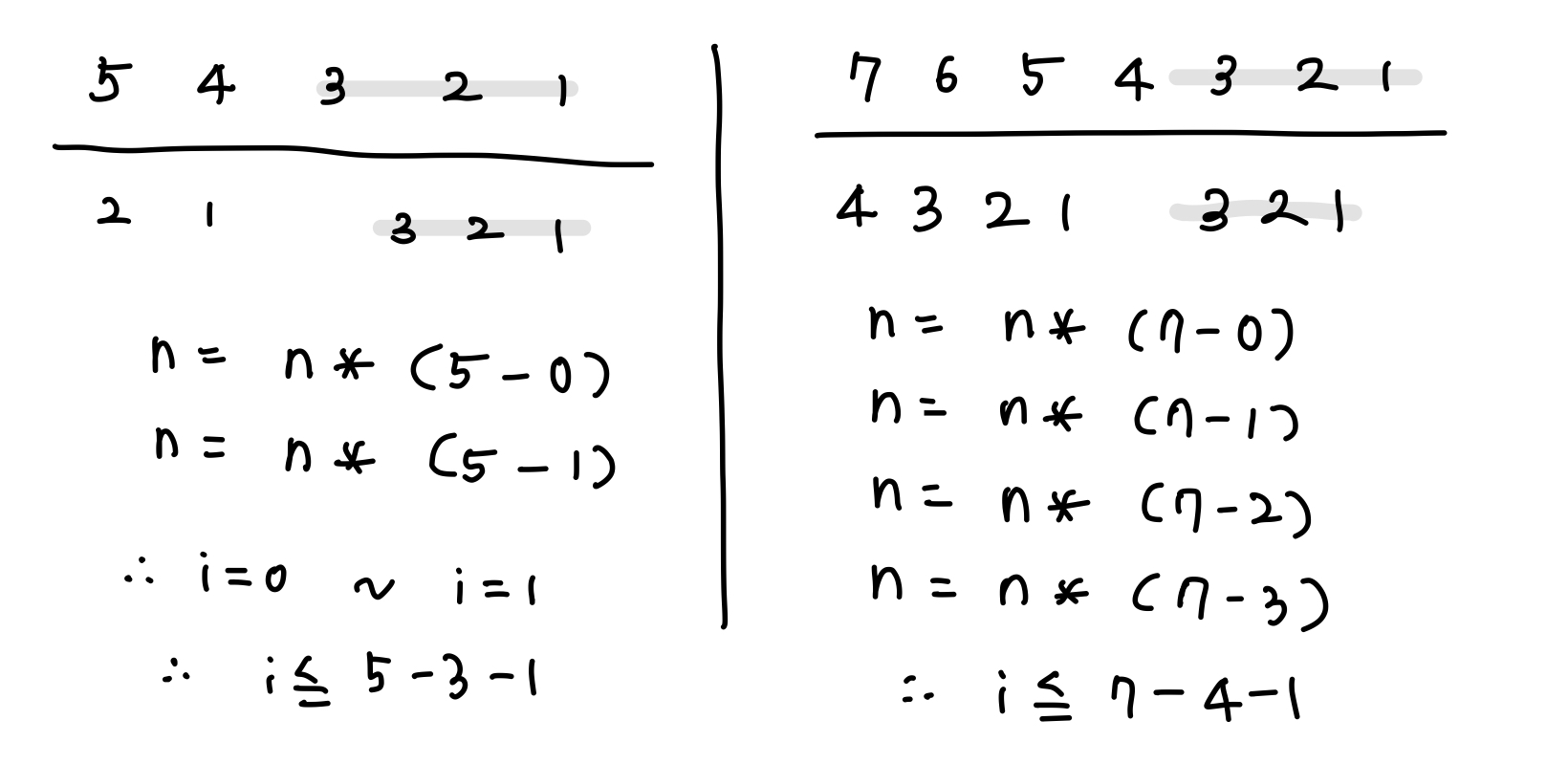 가 된다.
가 된다.
결과는 테스트 케이스는 성공, 그러나 제출하니까 몇개의 케이스가 실패했다.
내 풀이: 두번째 시도
class Solution {
public int solution(int balls, int share) {
int answer = 0;
double n = 1;
double m = 1;
if(balls == share) {
answer=(int)1;
} else {
for(int i=0; i<=balls-share-1; i++){
n*=(balls-i);
}
for(int i=balls-share; i>=1; i--) {
m*=i;
}
answer = (int)Math.round(n/m);
}
return answer;
}
}생각해보자. 테스트 케이스의 수들은 다 10의자리 이하 숫자들.
만약 balls와 share가 30, 20의 숫자를 갖는다면 어떻게 될까?
참고로 30!은 무려 265252859812191058636308480000000 의 값을 갖는다.
이 수를 int타입 변수에 담아주니 당연히 실패할 수 밖에.
doouble 타입으로 분자 n, 분모 m 을 설정해주고, 그 다음 n/m 값을 (int)Math.round 를 통해 double 타입을 int 타입으로 변환 해준다.
double 타입을 int 타입으로 형변환 할 때,
- (int)(n/m) -> 시도안해봄;;
- int val = n/m
val.intValue();
