희소 다항식끼리의 덧셈 구현하는 게 어렵다.

일단 temp 배열에서 exp이 같은 걸 어떻게 찾아내야 할까?
그리고 지수가 같아도 새로 항을 추가해야 하는 경우, 항이 존재하는 경우 계수만 더하는 경우로도 나눠야 한다.
주어진 다항식 A, B끼리의 지수 비교, 그리고 temp 배열 내에서 지수 존재 여부
일단 index가 0이면 temp에 지수가 존재하는지 볼 필요 없이 무조건 새 항을 하나 추가해야 한다.
일단 조건이
- this와 poly의 terms_가 exp의 오름차순으로 정렬되어 있다고 가정
- 하나의 다항식 안에 exp가 중복되는 term이 없다라고 가정
이므로 temp 배열 속 exp가 같은 게 있는지 검사할 필요가 없다.
예외가 있나? 없다.
구현 성공!!!!
근데 while 문을 각각 3번씩 돌려서 하나로 합칠 수 있을 것 같은데 생각 좀 더 해봐야겠다.
헷갈렸던 부분
while (i < this->num_terms_ || j < poly.num_terms_)에서 두 조건 중 하나만 false이면 빠져나오는 걸로 착각했는데 or 연산자가 둘 중 하나가 참이면 전체가 참이므로 계속 실행됐다. 따라서 두 조건 중 하나가 false면 빠져나오도록 하려면
while (i < this->num_terms_ && j < poly.num_terms_)로 해줘야 한다.
차수는 오름차순으로 정렬되어 있음.
차수가 7과 11이라면 차수 11인 배열에서는 더 이상 7과 더해질 수 있는 게 없다는 거니깐(오름차순 정렬이므로) 차수가 7인 것을 polynomial 배열에 추가.
더해서 만들어지는 polynomial도 차수가 정렬된 형태로 만들고 싶음.
강의 보니깐 거의 비슷하게 구현했다.

추가해야할 부분
float sum = terms_[i].coef + poly.terms_[j].coef;
if (sum != 0.0f)
{
temp.NewTerm(sum, terms_[i].exp);
if (sum != 0.0f)
{
temp.NewTerm(sum, terms_[i].exp);
}
i++;
j++;
}시간 복잡도
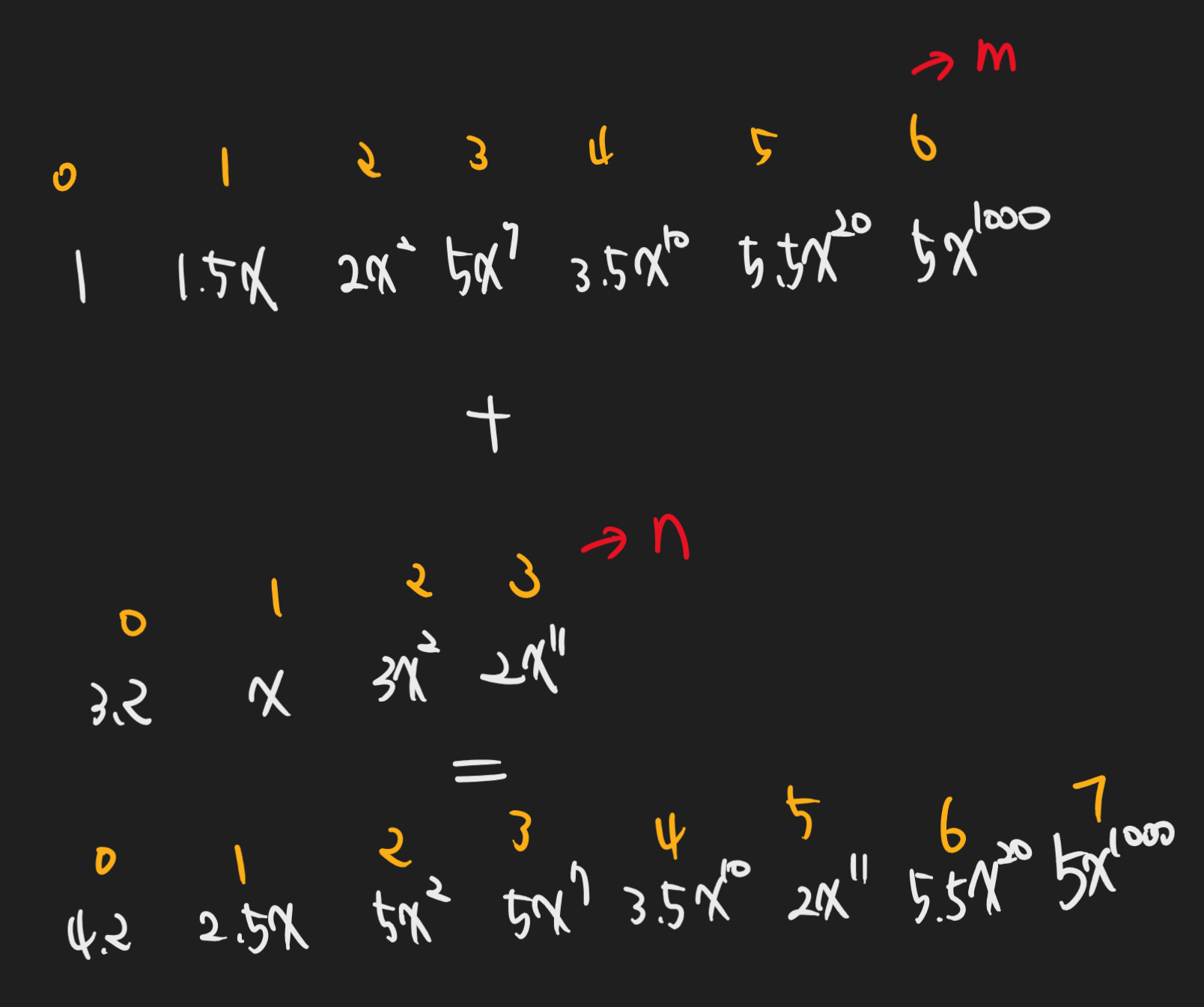
하나하나 찾는다면 O(m n)
각 항마다 n번씩 비교, 항이 총 m개이므로 m n번 비교
int i = 0, j = 0으로 두고 전진하는 경우
O(m + n)
NewTerm()에서의 시간 복잡도
최종적으로 받고 있는 capacity는 2^5
: 0 -> 1 -> 2 -> 4 -> 8 -> 16 -> 32
계속 호출해서 최종적으로 가장 크게 확보한 메모리: n
메모리를 증가시키는 작업: 6번
메모리를 추가하는 연산: O(log n)
메모리를 증가시키는 연산 분석 시, 1-2번이 중요하지 메모리를 얼마나 크게 받아오는지는 상관이 없음.
= 메모리를 1000개를 받아오든 10000개를 받아오든 똑같은 시간이 걸림.
= 연산해서 받아오는 메모리 양보다 연산 횟수가 중요함.
x^2 -> 그냥 다항식 배열로 구현
차수는 가장 높은 차수를 포함하고, 항의 개수는 적은 경우: 희소 다항식 구조 사용하면 훨씬 효율적
출처: 홍정모 연구소